동료를 신뢰해야 할까? 배반해야 할까? 이런 궁극적인 갈등을 다룬 문제에 '죄수의 딜레마(Prisoner's Dilemma)'라는 문제가 있다.
0. 목차
- 죄수의 딜레마
- 죄수의 딜레마를 게임의 상황에 적용
- 죄수 3명의 딜레마

1. 죄수의 딜레마
나는 은행 강도 용의자 2명 중 한 명으로 체포되었다. 하지만 형사는 불법 무기를 소지하고 있다는 정황상 증거만 찾았을 뿐 결정적인 증거를 찾지 못한 상태이다. 나와 공범자는 자백을 하지 않고 침묵을 지키고 있다. 이대로라면 증거 불충분으로 강도죄로 처벌받지 않아도 되고 불법 무기 소지죄의 처벌만 1년이다. 그래서 형사는 우리에게 자백을 받아내기 위해 2명을 취조실로 따로 불러 다음과 같이 말했다. 둘 다 자백하지 않으면 불법 무기 소지죄로 1년, 둘 다 강도죄를 자백하면 5년이다. 단, 공범자가 자백하고 내가 침묵을 지킨다면, 공범자는 석방되고 나의 형기는 10년이다. 반대로 내가 자백하고 공범자가 침묵을 지킨다면, 나는 석방되고 공범자의 형기는 10년이다.
그리고 수사관은 같은 이야기를 공범에게도 했음을 용의자에게 전했다. 2명의 용의자에게 가장 이득인 상황은 서로 계속 침묵해서 형기를 2명 모두 1년으로 하는 것이다. 그러나 공범이 만약 배반하고 자백을 하면, 공범만 석방되고 자신은 형기가 10년이 된다. 그런 상황을 겁내서 2명이 모두 자백하면 형기는 2명 모두 5년이 된다. 이 상황에서 용의자는 어느 쪽을 택해야 할까?
| - | 공범자 | ||
| 침묵 | 자백 | ||
| 나 | 침묵 | 1년 | 10년 |
| 자백 | 석방 | 5년 | |
1-1. 아직까지 통일된 견해는 없다.
'죄수의 딜레마(Prisoner's dilemma)'의 상황에서는 어떤 선택을 해도 그 선택에 대한 논리적인 이유를 설명할 수 있다. 그래서 어떤 선택을 해야 할지에 대해서 합리적으로 판단하지 못하게 되는 것이다. '죄수의 딜레마'는 1950년에 미국의 수학자인 '앨버트 터커(Albert Tucker)'에 의해 고안되었는데 이 딜레마가 고안되고 나서 많은 연구자들이 어느 쪽이 좋은지에 대해 많은 의견을 내놓았지만 아직까지 통일된 견해가 없는 상황이다. 단순한 '손실, 이득 판단' 뿐만 아니라 '도덕관', 상대방의 '이성적 판단 능력'과도 복잡하게 얽혀 있기 때문이다.
2. '죄수의 딜레마'를 게임의 상황에 적용
이번에는 '죄수의 딜레마'를 게임의 상황에 적용시켜 보자. 게임 주최자와 게임 참가자 2명이 하는 카드 게임으로 규칙은 다음과 같다. 나와 상대방은 각각 '협력' 카드와 '배반' 카드를 가지고 있다. 게임 주최자의 신호가 동시에 게임 참가자들은 '협력'과 '배반'카드 중 하나를 테이블에 내야 한다. 카드의 조합에 따라 받는 상금은 다음과 같이 달라진다. 둘 다 '협력 카드'를 낸 경우 3만 원씩, 둘 다 '배반 카드'를 낸 경우 1만 원씩, 둘이 '협력 카드', '배반 카드'로 갈린 경우 '배반 카드'를 낸 사람에게만 5만 원을 주고 '협력 카드'를 낸 사람에게는 한 푼도 주지 않는다. 나는 어떤 선택을 해야 할까? 이 딜레마의 정답 역시 어떤 선택도 '좋은 선택'이 될 수 있다는 것이다.
| - | 상대방 | ||
| 협력 | 배반 | ||
| 나 | 협력 | 둘 다 3만 원 | 0원 (상대방 5만 원) |
| 배반 | 5만 원 (상대방 0원) | 둘 다 1만 원 | |
2-1. 아직까지 통일된 견해는 없다.
이 게임의 최고 상금은 5만원이다. 따라서 5만 원을 받을 수 있는 유일한 방법은 내가 협력을 내고 상대방이 배반을 내는 경우뿐이다. 다음처럼 생각할 수도 있다. '배반 카드'를 내는 것은 최소 1만 원 이상을 보장받을 수 있는 유일한 방법이다. 따라서 '배반 카드'을 내는 것이 좋은 전략이 될 수 있는 것이다.
하지만 '협력 카드'를 내는 것이 좋다고 생각할 수도 있다. 이 게임의 목적은 어떻게 하면 가장 상금을 많이 얻을 수 있는가에 대한 게임이다. 따라서 모두 협력을 내는 경우에 참가자에게 주어지는 보상의 합이 가장 크기 때문에 '협력 카드'를 내는 것이 좋다고 생각할 수도 있다는 것이다.
하지만 이 게임을 여러 번 되풀이할 때에는 어떤 선택을 해야 할까? 예를 들어 이 게임을 300번 한다고 했을 때 가장 많은 상금을 가져가려면 어떻게 해야 할까? 1984년, 어떻게 하면 가장 많은 상금을 가져갈 수 있을지 알아보기 위해 경제학, 정치학, 심리학 등의 전문가가 모여 이 게임을 컴퓨터끼리 반복하는 콘테스트가 열렸었다. 그 결과 가장 좋은 전략은 처음에 '협력 카드'를 내고 상대방이 '배반 카드'를 낼 경우 다음에 '배반 카드'를 내서 보복하고 '협력 카드'를 내면 다음에 '협력'카드를 내면 된다는 것이었다. 이 '보복 전략'이 항상 최강은 아니지만 다른 전략에 비해 효과적이었다고 한다.
3. 죄수 3명의 딜레마
흉악한 범죄단 3명 A, B, C가 있었다. 어느 날, 그들은 전설의 보물섬의 존재를 알아내고, 드디어 섬 안에 잠자는 보물이 있다는 사실까지 알게 되었다. 그러나 보물을 가지러 가는 도중에 3명 모두 체포되었다. 체포된 3명은 지금까지 수많은 흉악 범죄를 거듭 저지른 죄목으로 처형당하게 되었다. 하지만 보물이 있는 곳을 아는 사람은 3명뿐이므로, 3명 모두 처형하면 보물이 있는 곳을 아는 사람이 사라진다. 그래서 3명 가운데 2명은 처형하고, 1명은 보물이 있는 곳을 가르쳐주는 것을 조건으로 석방하기로 결정되었다.
3명 가운데 누가 석방될지는 이미 제비뽑기로 정해져 있다고 한다. 그러나 범인들은 석방되는 것이 누구인지 알지 못한다. 이 경우, 범인 A가 석방될 확률은 1/3임을 알 수 있다.
3-1. 범인 A의 처형될 확률은 줄었을까?
범인 A는 교도관에게 "나는 처형되나요?"라고 물었지만, 교도관은 "그것은 비밀입니다."라고 대답할 뿐이었다. 그래서 범인 A는 교도관에게 "3명 중 2명은 처형되기 때문에, 범인 B와 범인 C 가운데 적어도 1명은 처형될 것이다 그 1명을 나에게 가르쳐 주어도 나 자신이 처형될지 아닐지는 알지 못한다. 그러니 B, C 가운데 누가 처형되는지 알려달라."고 했다. 그러자 교도관은 'B는 처형됩니다."라고 대답했다. 범인 A는 B가 처형된다는 것을 알고, 처형될 다른 한 명은 A 또는 C이므로, 자신이 처형될 확률이 1/2이 되었다고 생각하고 기뻐했다. 과연 이 해석이 옳을까?
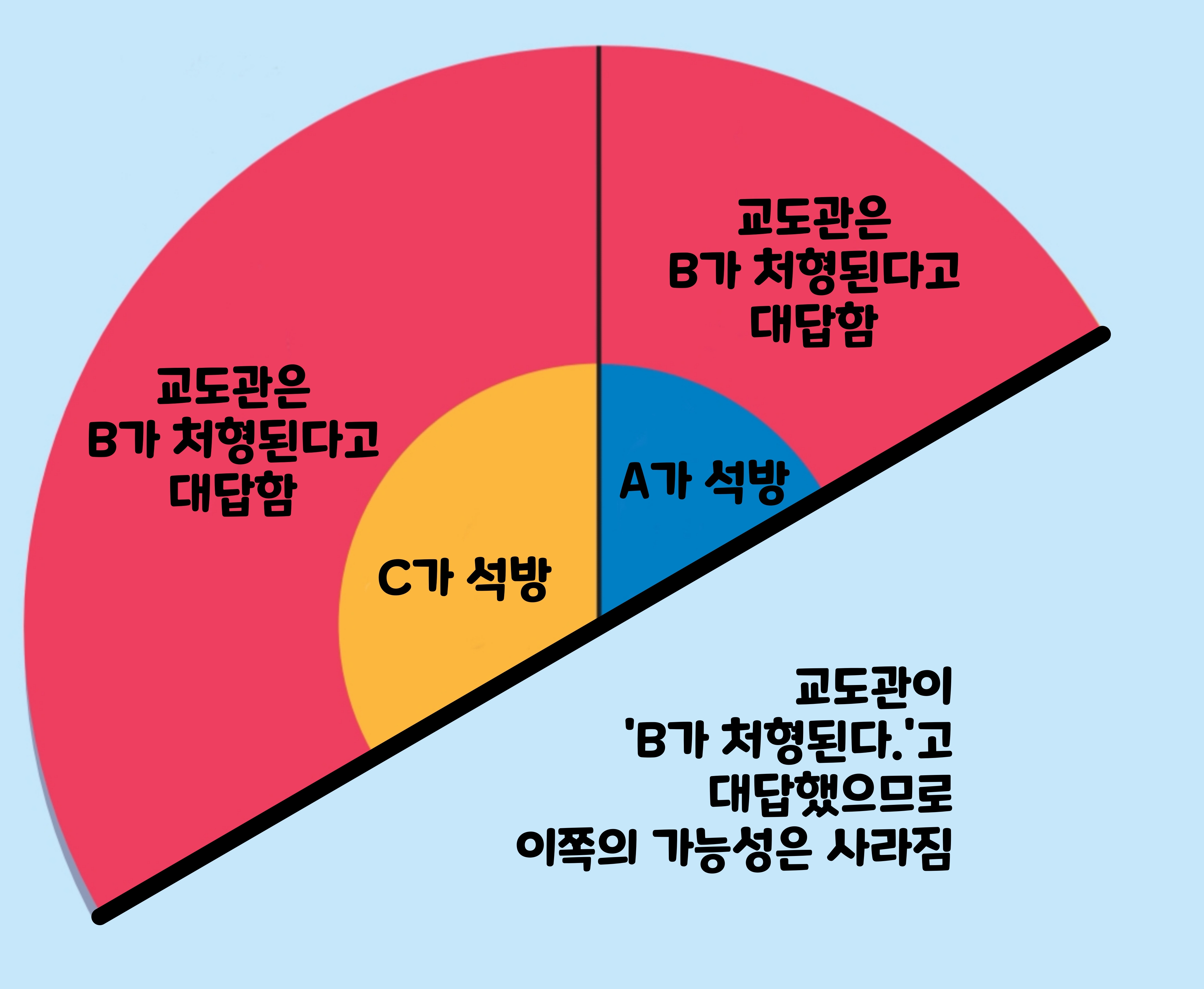
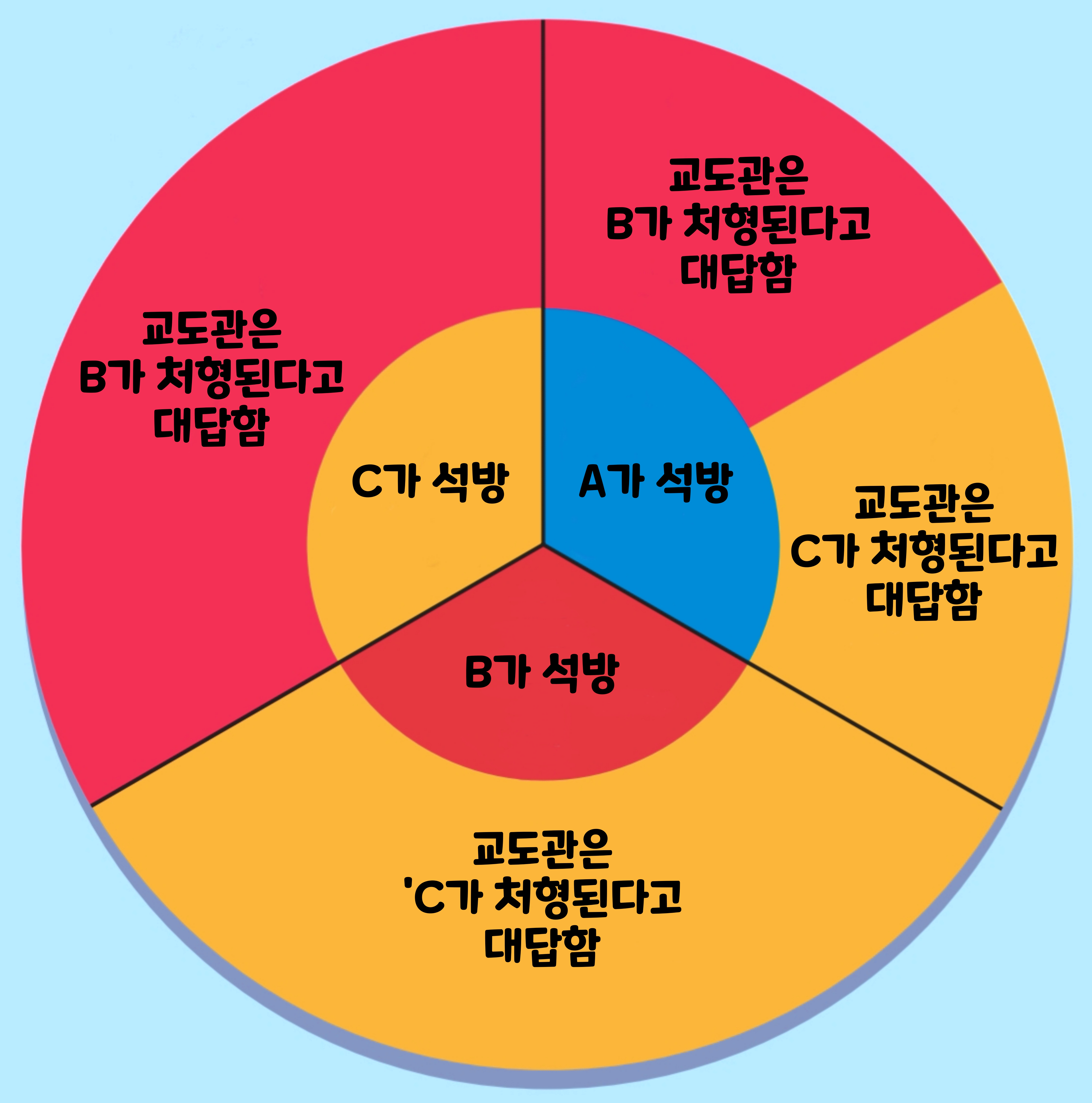
- A가 석방될 경우: 아무 정보가 없는 경우에는 범인 A가 석방될 확률이 1/3이었다. 여기서 만약 범인 A가 석방될 몸이었을 경우를 생각해 보자. 이 경우, B와 C가 모두 처형된다. 따라서 교도관이 범인 A에게 'B는 처형된다.'고 말할 확률과 'C는 처형된다.'라고 말할 확률은 같다. 즉, B라고 하든 C라고 하든, 교도관에 달려 있으므로 확률은 1/2씩으로 간주할 수 있다.
- A가 석방될 경우: B가 석방될 경우, 교도관은 A라고는 대답할 수 없으므로 'C가 처형된다'고 대답한다.
- C가 석방될 경우: C가 석방될 경우, 교도관은 A라고는 대답할 수 없으므로 'B가 처형된다'고 대답한다.
그런데 실제로 교도관은 범인 A에게 'B가 처형된다.'고 했다. 아래의 그림을 보면 교도관이 '범인 A에게 B가 처형된다.'고 가르쳐 줄 패턴은 C가 석방될 경우의 전부와 A가 석방될 경우의 절반임을 알 수 있다. 이 2가지 패턴을 합친 것 가운데 C가 석방될 확률은 2/3이다. 즉, 범인 A은 여전히 1/3의 확률로 석방될 운명에 있다. 따라서 A가 석방될 확률이 높아졌다고 기뻐한 것은 헛된 일이었다.