우리는 집단에서 어떤 일을 결정할 때 민주적인 방법으로 의사 결정을 하기 위해 '투표(Vote)'를 한다. 많은 경우 투표로 결정된 결과가 자신의 생각과 다르다고 해도 그 결과를 받아들인다. 대부분의 사람들은 투표를 합리적인 방법이라고 생각한다. 하지만 투표의 방식에 따라서 불합리한 결과가 도출될 수도 있다.
0. 목차
- 토너먼트 방식의 다수결 방식
- 단기 투표 방식
- 리그전 결선 방식
- 상위 양자 결선 투표 방식
- 순위 평점 방식
- 결론: 결점이 없는 투표 방식은 없다.

1. 토너먼트 방식의 다수결 방식
어느 날 친구 3명(A, B, C)이 모여 무엇을 먹을지에 대해 이야기를 나누고 있었다. 점심 메뉴의 후보는 햄버거, 떡볶이, 짜장면이었다. 이 세 가지 후보 중에서 다수결로 메뉴를 정하기로 했다. 이들은 먼저 햄버거와 떡볶이 중에서 투표를 했더니 '햄버거 2표', '떡볶이 1표'로 햄버거가 이겼다. 다음에는 승자인 햄버거와 짜장면 중에서 투표를 했더니 '햄버거 1표', '짜장면 2표'가 나왔다. 여기서 똑똑한 사람이라면 뭔가 이상했음을 느꼈을 것이다. 무엇이 잘못됐을까?
먹고 싶은 음식의 순위는 다음 표와 같았다.
| - | 햄버거 | 떡볶이 | 짜장면 |
| A | 2 | 1 | 3 |
| B | 1 | 3 | 2 |
| C | 3 | 2 | 1 |
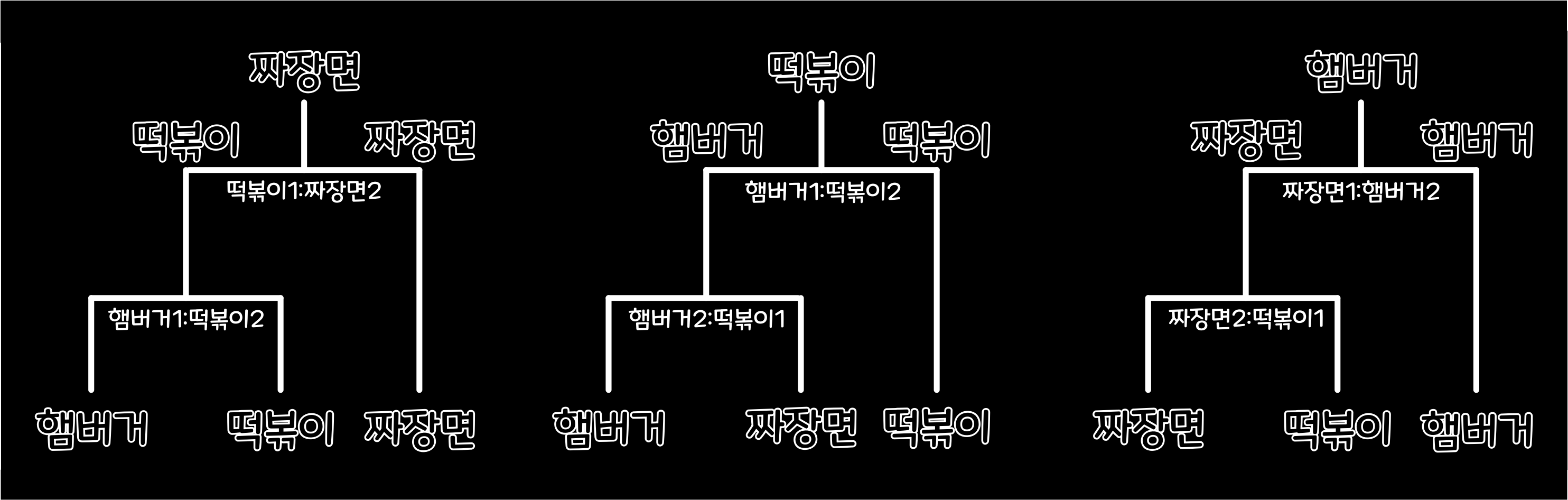
이처럼 '토너먼트 방식'의 투표 방식에서는 투표의 순서에 따라 어느 것이나 최종 승자가 되는 일이 나타날 수 있다.
2. 단기 투표 방식
이번에는 친구 7명(A, B, C, D, E, F, G)이 모여있다. 이번에도 햄버거, 떡볶이, 짜장면 중에서 각자 먹고 싶은 음식을 하나씩 고르기로 했다. (이처럼 복수의 선택지에서 하나만 선택하는 방식을 '단기 투표 방식'이라고 한다.) 그러자 햄버거 3표, 떡볶이 2표, 짜장면 3표가 나왔다. 가장 먹고 싶은 음식으로 햄버거가 선택되었다. 하지만 가장 먹기 싫은 음식을 투표하자 햄버거 4표 떡볶이 2표, 짜장면 2표가 나왔다. 가장 먹기 싫은 음식도 햄버거가 선택되었다. 어떻게 이런 결과가 있을 수 있을까? '단기 투표 방식'에는 아무런 문제가 없는 것처럼 보이지만 이 투표 방식 또한 문제가 있기 때문이다. 무엇이 잘못됐을까?
먹고 싶은 음식의 순위는 다음과 같았다.
| - | 햄버거 | 떡볶이 | 짜장면 |
| A | 1 | 2 | 3 |
| B | 1 | 2 | 3 |
| C | 1 | 3 | 2 |
| D | 3 | 1 | 2 |
| E | 3 | 1 | 2 |
| F | 3 | 2 | 1 |
| G | 3 | 2 | 1 |
이처럼 '단기 투표 방식'에서는 집단이 가장 나쁘다고 생각한 것이 가장 좋은 것으로 선택되는 경우가 있다.
3. 리그전 결선 방식
그래서 7명의 친구들은 '단기 투표 방식'에 문제가 있음을 느끼고 모든 메뉴 후보를 1:1로 비교해 승자를 정해 보기로 했다. 이처럼 1:1로 비교해 보는 방식을 '리그전 결선 방식'이라고 한다. 그러자 '떡볶이4:햄버거3', '떡볶이4:짜장면3', '햄버거4:짜장면3'이 나왔다. 하지만 '리그전 결성 방식'에도 단점이 있다. 선택지의 수가 많아질수록 투표의 횟수도 심하게 늘어난다는 것이다. 예를들어 12개의 음식 후보가 있다면 190회의 투표를 해야 한다.
4. 상위 양자 결선 투표 방식
'단기 투표 방식'의 결점을 보안하기 위해 '상위 양자 결선 투표 방식'이라는 것도 나왔다. '상위 양자 결선 투표 방식'이란 1위의 득표수가 일정 조건에 미치지 못하면 상위 후보 몇 개를 대상으로 다시 투표를 진행하여 최종 결정하는 방식이다. 올림픽 개최지를 결정하는 투표 등에 이 방식이 쓰이고 있다. 하지만 이 방식도 '단기 투표 방식'의 단점을 완전히 보완할 수는 없다.
5. 순위 평점 방식
그래서 이 한계를 극복하기 위해 프랑스의 수학자 '장샤를 드 보르다(Jean-Charles de Borda, 1733~1799)'는 '순위 평점 방식'을 고안했다. '순위 평점 방식'이란 순위를 투표하고 순위에 해당하는 점수를 부여하여 가장 높은 점수를 받은 것으로 최종 결정하는 투표방식이다. 이 점수를 '보르다 점수(Borda Score)'라고 한다. 하지만 이 방식도 결점이 있다.
다음과 같은 경우를 생각해보자.
| - | 햄버거 | 떡볶이 | 짜장면 | 피자 |
| A | 4위 (1점) | 3위 (2점) | 2위 (3점) | 1위 (4점) |
| B | 1위 (4점) | 4위 (1점) | 3위 (2점) | 2위 (3점) |
| C | 2위 (3점) | 1위 (4점) | 4위 (1점) | 3위 (2점) |
| D | 4위 (1점) | 3위 (2점) | 2위 (3점) | 1위 (4점) |
| E | 1위 (4점) | 4위 (1점) | 3위 (2점) | 2위 (3점) |
| F | 2위 (3점) | 1위 (4점) | 4위 (1점) | 3위 (2점) |
| G | 4위 (1점) | 3위 (2점) | 2위 (3점) | 1위 (4점) |
| 합계 | 17점 | 16점 | 15점 | 22점 |
| 순위 | 2위 | 3위 | 4위 | 1위 |
피자가 가장 높은 점수가 나왔다. 하지만 피자를 제외하고 순위를 다시 매겨보면 순위가 또 바뀐다.
| - | 햄버거 | 떡볶이 | 짜장면 |
| A | 3위 (1점) | 2위 (2점) | 1위 (3점) |
| B | 1위 (3점) | 3위 (1점) | 2위 (2점) |
| C | 2위 (2점) | 1위 (3점) | 3위 (1점) |
| D | 3위 (1점) | 2위 (2점) | 1위 (3점) |
| E | 1위 (3점) | 3위 (1점) | 2위 (2점) |
| F | 2위 (2점) | 1위 (3점) | 3위 (1점) |
| G | 3위 (1점) | 2위 (2점) | 1위 (3점) |
| 합계 | 13점 | 14점 | 15점 |
| 순위 | 3위 | 2위 | 1위 |
이처럼 '순위 평점 방식'은 어떠한 이유로 1위를 채용할 수 없을 때, '보르다 점수'를 어떻게 설정하느냐에 따라 승자가 바뀌는 경우가 있다는 한계가 있다.
6. 결론: 결점이 없는 투표 방식은 없다.
그러면 결점이 없는 투표 방식은 없는 걸까? 그렇다. 이미 1951년에 미국의 경제학자 '케네스 애로(Kenneth Arrow, 1921~2017)'가 '완전히 민주적인 투표방식은 존재하지 않는다.'는 사실을 수학적으로 증명해냈다. 하지만 이러한 투표 방식의 결점에도 불구하고, 민주주의에서는 집단의 의사결정 수단이 필요하다. 결국 우리는 각각의 투표 방식의 한계와 특성을 잘 이해하고 목적에 맞는 투표 방식을 선택할 수밖에 없는 것이다.