0. 목차
- 동시성의 불일치
- 시간의 흐름이 느려진다.
- 시간이 느려지는 것은 '피장파장'
- 속도의 덧셈
- 공간이 줄어든다.
- 공간이 줄어드는 것도 '피장파장'
- 상대성 이론을 체험하는 입자
- 질량이 커진다.
- 질량이란 무엇인가?
1. 동시성의 불일치
'상대성 원리(Relativity Principle)'와 '광속도 불변의 원리(Principle of Constancy of Light Velocity)'를 생각함으로써 '특수 상대성 이론(Special Theory of Relativity)'이 유도된다. 이 두 가지를 토대로 '특수 상대성 이론'의 세계로 들어가 보자. 상대성 이론에서는 '관측자'가 매우 중요하므로, 이 점에 주의하면서 읽어나가면 이해하기 수월할 것이다.
1-1. '나의 동시'와 '당신의 동시'는 다르다
다음과 같은 예를 생각해 보자. 달 표면에서 봤을 때, 오른쪽 방향으로 광속에 가까운 '일정한 속도'로 날아가고 있는 우주선이 있다. 우주선 한가운데에는 광원이 있고 좌우에는 빛 검출기가 설치되어 있다. 빛 검출기에 빛이 들어가면, 각각 연결되어 있는 발광탄 발사 장치에 신호를 전한다.
- 우주선 내부의 관측자 입장: 우선 우주선 안에 있는 관측자 A가 보는 상황을 떠올려 보자. '상대성 원리'에 따르면, A에게 움직이고 있는 것은 달이고, 우주선은 정지해 있는 것과 같다. 또 '광속도 불변의 원리에 따라 빛은 좌우로 똑같은 속도로 나아가기 때문에 같은 거리에 있는 좌우의 빛 검출기에 동시에 도달한다. 즉, 우주선 안에 있는 관측자 A가 보면 좌우의 발광탄은 '동시에' 발사된다.
- 달표면 기지의 관측자 입장: 이번에는 달표면 기지의 관측자 B가 보는 상황을 떠올려 보자. '광속도 불변의 원리'에 따르면, 우주선의 운동과는 관계 없이 달 표면에서 볼 때 좌우의 빛의 속도는 같다. 그런데 우주선이 광속에 가까운 속도로 오른쪽으로 날아가고 있기 때문에, 왼쪽의 빛 검출기는 빛에 다가가고, 오른쪽의 빛 검출기는 빛에서 멀어져 간다. 결국, 달 표면의 관측자 B가 보면, 왼쪽의 빛 검출기에 먼저 빛이 들어가므로, 발광탄은 왼쪽이 먼저 발사되고 오른쪽 발광탄은 늦게 발사된다.
즉, 우주선 안에 있는 관측자 A에게는 동시였던 발광탄 발사가 관측자 B에게는 동시가 아니게 된다. 이를 '동시성의 불일치'라고 한다. 또는 관측자 A, B는 서로 '다른 시간'을 가지고 있다고도 말할 수 있다. 일상적인 감각으로 생각하면, 이 결론은 말이 되지 않아 보인다. 하지만 '상대성 원리'와 광속도 불변의 원리'가 옳다면 자연스럽게 나오는 결론이다.

2. 시간의 흐름이 느려진다.
지금부터는 '시간의 흐름이 느려진다'는 '특수 상대성 이론'의 핵심으로 다가가보자. 달 표면에서 봤을 때 '초속 약 24km(광속의 약 80%)'로 오른쪽으로 날아가는 우주선을 생각해 보자. 우주선 안과 달 표면에는 '빛 시계'가 설치되어 있다. '빛 시계'란 위와 아래에 거울이 달려 있고, 그 사이를 오가는 방식으로 시간을 재는 장치이다. '빛 시계'의 아래쪽 거울에는 광원이 붙어 있고, 아래쪽 거울에서 출발한 빛이 위쪽 거울에 닿는 순간이 1초 경과를 의미한다.
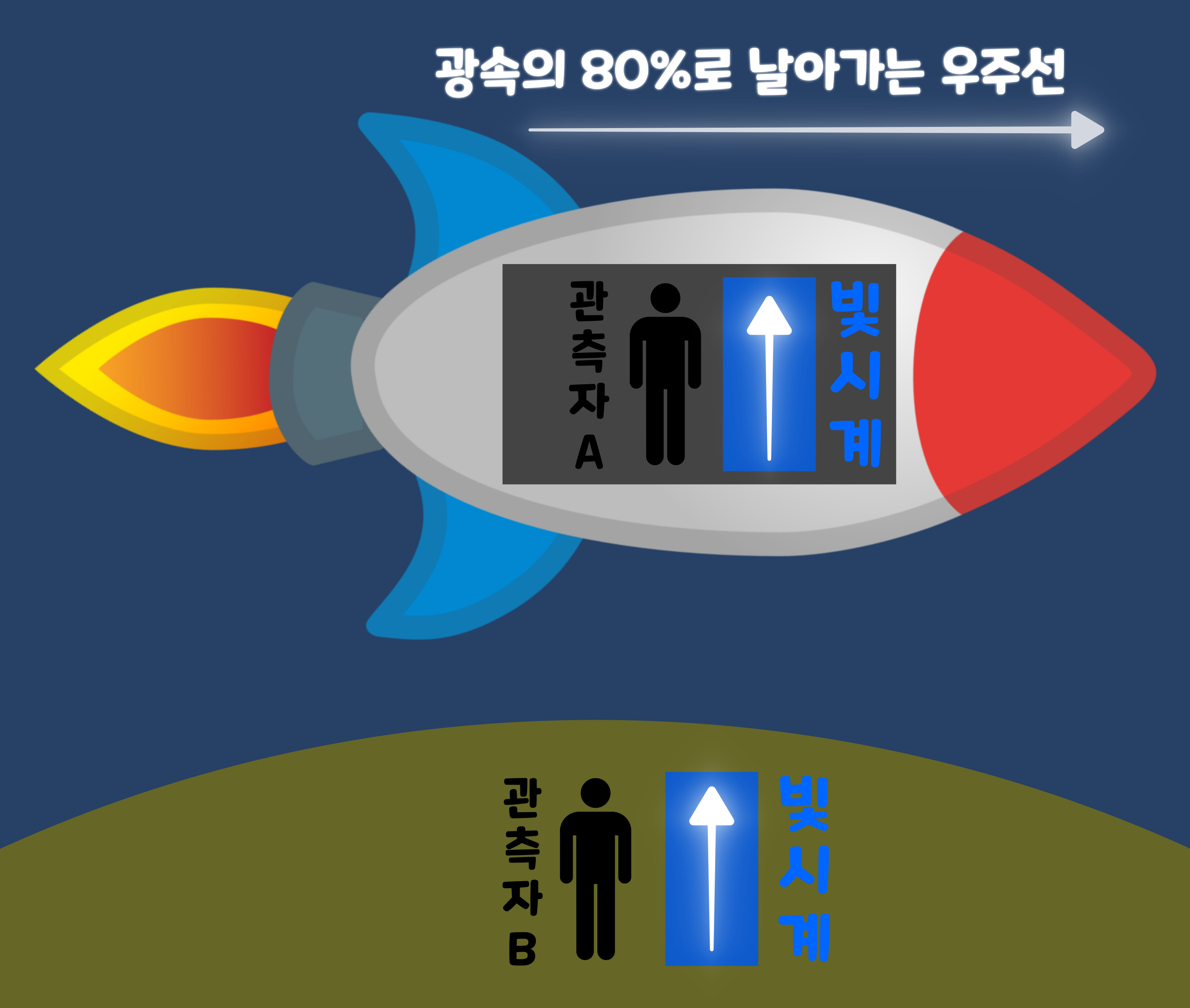
2-1. 우주선 안에 있는 관측자 A의 입장
먼저 우주선의 관측자 A가 보는, 우주선 안에 있는 빛 시계에 대해 생각해 보자. '상대성 원리'에 따르면 우주선 안은 정지해 있는 것과 다름없기 때문에, '빛 시계'의 광원에서 나온 빛은 위로 향한다. 또 '광속도 불변의 원리'에 따라 이때의 빛은 초속 30만 km로 위로 날아간다. 우주선은 정지해 있는 것과 마찬가지이므로, 달 표면에서 '달 표면의 시계'를 보고 있는 것과 아무런 차이가 없다. 즉, 우주선의 관측자 A에게는 주위의 시간의 흐름은 언제나 그대로이다.
2-2. 달 표면에 있는 관측자 B의 입장
이번에는 달 표면에 있는 관측자 B의 입장에서 생각해 보자. 우주선은 오른쪽으로 나아간다. 따라서 우주선 안에 있는 빛 시계의 광원에서 나온 빛은 위쪽의 거울에 도달할 때까지 비스듬히 나아가는 것처럼 보인다. 또 '광속도 불변의 원리'에 따르면 빛은 초속 30만 km로 나아간다. 여기에서 중요한 것은 빛 시계의 높이보다 빛의 비스듬한 움직임 쪽의 길이가 길다는 점이다.
한편, 달 표면에 있는 빛 시계'의 빛도 같은 속도로 나아간다. 1초 뒤 달 표면에 있는 빛 시계의 빛은, 달 표면의 빛 시계의 빛보다 늦게 위쪽 거울에 닿는다. 하지만 이 순간 달 표면에서 우주선을 보면, 우주선 안에 있는 빛 시계의 빛은 위쪽 거울에 도달하지 않았다. 빛 시계의 높이보다. '빛의 비스듬한 움직임' 쪽의 길이가 길기 때문이다. 따라서 우주선의 빛 시계의 빛은, 달 표면의 빛 시계의 빛보다 늦게 위족 거울에 닿는다. 빛이 위쪽 거울에 닿을 때가 우주선에서의 1초이므로, 달 표면의 관측자 B가 볼 때 우주선의 1초는 달표면의 1초보다 길어진다. 즉, 달 표면의 관측자가 봤을 때 우주선의 시간이 느려졌다.
2-3. 광속에 가까워질수록 시간의 흐름이 느려진다.
매우 기묘하지만, 이는 '상대성 원리'와 '광속도 불변의 원리'로부터 자연스럽게 나오는 결론이다. 이 2개의 원리가 성립하도록, 우주가 시간의 흐름을 느리게 하는 이치를 가지고 있다고 말해도 좋을 것이다. 결론적으로, 우주선의 속도가 광속에 가까워질수록 시간의 흐름은 점점 느려진다.
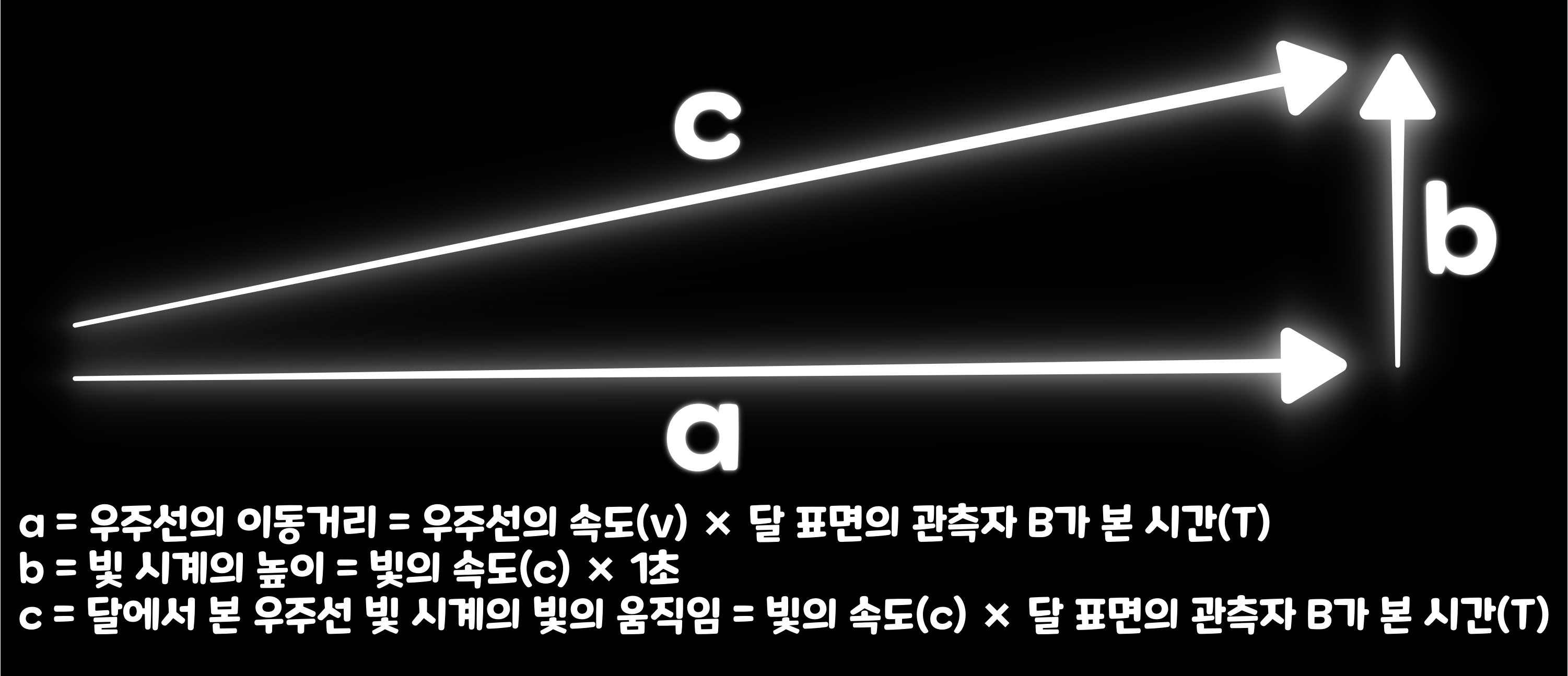
우주선의 시간이 얼마나 느려지는가는 '피타고라스 정리(Pythagorean theorem)'를 통해 구할 수 있다. 달 표면의 관측자 B가 볼때, T초 후에 우주선 빛 시계의 빛이 빛 검출기에 들어간다. 그러면 달 표면의 빛 시계로 T초의 시각에 우주선의 관측자 A의 빛 시계는 1초를 가리키게 된다. 즉, 우주선의 시간은 달표면의 시간과 비교해서 T배 느려진다. 아래와 같은 직각삼각형을 생각하면 피타고라스 정리로 느려진 시간 'T'를 구하는 공식을 구할 수 있다. 예컨대 우주선의 속도가 광속의 80%라면, v에 0.8c를 대입하면 된다. 그러면 T는 1.67이 되고, 달 표면에서 1.67초가 지났을 때 우주선에서는 1초밖에 지나지 않게 된다. 피타고라스 정리에 의하여 a2+b2=c2, 따라서 (cT)2=(vT)2+c2식에서 T를 구하면 된다.

3. 시간이 느려지는 것은 '피장파장'
3-1. 우주선 관측자 입장에서는 달 표면의 시간이 느려진다.
지금까지 광속에 가까운 속도로 날아가는 우주선을 '달 표면'에서 보면, 우주선의 시간의 흐름이 느려짐을 알아보았다. 하지만 상대성 이론은 더욱 놀라운 것을 말하고 있다. 같은 상황에서, 이번에는 반대로 '우주선에서' 달표면을 관측하면, 달 표면의 시간의 흐름이 느려진다. 즉, 시간이 느려지는 것은 '피장파장(Equality)'이 된다.
엇갈려 지나가는 2대의 우주선이 '등속 직선 운동'을 하는 상황을 떠올려 보자. 등속 직선 운동을 하는 두 관측자 가운데, 어느 쪽이 정말로 운동하고 있는지를 알 수 있는 방법은 없다. 어디까지나 등속 직선 운동은 '피장파장'이다. 이것이 '상대성 원리'이다. 즉 '상대성 원리'에 따르면, 우주선에서 볼 때도 같은 논리가 적용되기 때문에 이번에는 달에서의 시간이 느려진다.
3-2. 서로의 시간이 느려지는 것은 '동시성의 불일치' 때문이다.
하지만 '양쪽 시계의 흐름이 모두 느려지는 것'이 모순이라고 생각될지도 모른다. 이 혼란을 해결하는 열쇠는 '동시성의 불일치'이다. 광속에 가까운 속도로 운동하고 있는 우주선의 '관측자 A'와 달 표면 기지의 '관측자 B'의 '동시'는 일치하지 않는다.
다시 한 번 '동시'에 주의하면서 바꾸어 생각해 보자. 우주선 빛 시계의 광원에서 빛이 나오는 순간에 우주선과 달 표면의 시계를 0에 맞춘다. 우주선의 시계가 1초 지났을 때, '우주선의 관측자가 동시에' 달 표면 시계를 보면, 달 표면의 시계는 아직 1초가 지나고 있지 않다. 즉, 달 표면의 시간이 느려진다. 한편, 우주선의 시계가 1초 지났을 때, '달 표면의 관측자가 동시에' 달표면의 시계를 보면, 이 시계는 1초가 지난 상태에 있다. 우주선의 시간이 느려지는 것이다. 즉, 우주선에 있는 관측자의 동시와 달 표면에 있는 관측자의 동시가 서로 일치하지 않기 때문에, 두 사람은 각각 다른 것을 비교하고 있다. '상대편 시계의 진행이 느리다'는 서로의 주장은 둘다 맞는 것이다. 결국, 시간이 느려지는 것은 '피장 파장(Equality)'인 셈이다.
4. 속도의 덧셈
4-1. 상식적인 속도 계산은 맞지 않는다.
'상대성 이론'은 '속도 계산'에서도 상식과 다른 결론을 이끌어 낸다. '초속 20만 km로 지구 위를 날아가는 '모선(Mother Ship)'을 생각해 보자. 모선 앞 끝의 광원에서는 빛이 나온다. 그런데 '광속도 불변의 원리'에 따르면, 모선에 있는 관측자가 볼 때 빛은 초속 30만 km로 모선의 앞으로 나아간다. 또 '광속도 불변의 원리'에 따르면, 같은 빛을 달 표면의 관측자가 볼 떄도 초속 30만 km로 모선과 같은 방향으로 나아갈 것이다.
이때, '상식적인 속도 계산(뉴턴 역학의 계산)'에서는 달 표면에서 본 빛의 속도는 '초속 20만 km(모선의 속도)'+ '초속 30 km(모선 관측자가 본 빛의 속도) = 초속 50만 km'가 될 것이다. 즉, '광속도 불변의 원리'가 옳다는 것은 상식적인 속도 계산이 틀리다는 것을 의미한다.

4-2. 속도 계산에서는 '보는 입장'이 중요하다.
운동하는 우주선의 경우에도 빛의 속도에 가까워지면, 상식적인 속도 계산이 성립하지 않게 된다. 지구 표면에서 볼 때, 초속 20만 km로 오른쪽으로 날아가는 모선을 생각해 보자. 그 모선의 활주로에서, 모선에 대해 초속 20만 km의 속도로 발진하는 우주선이 있다. 그러면 '상식적인 속도 계산(뉴턴 역학의 계산)'에서, 지구 표면에서 본 우주선의 속도는 '초속 20만 km + 초속 20만 km = 초속 40만 km'가 된다. 하지만 상대성 이론에 따르면, 이 우주선의 속도는 27.7만 km밖에 되지 않는다.
그러면 '상식적인 계산'에서 무엇이 잘못되었을까? 그것은 '입장이 다른 시간과 거리를 근거로 해서 속도'를 더했기 때문이다. 즉, 올바른 속도 계산을 하려면, 먼저 '누가 본 속도인가'를 명확히 할 필요가 있다. 위의 식에서 첫 번째 항의 초속 20만 km는 지구 표면에서 본 모손의 속도이다. 한편, 두 번째 항의 초속 20만 km는 모선에서 본 우주선의 속도이다. 상대성 이론에 따르면, 시간과 거리는 관측자에 따라 변화한다. 따라서 위의 식처럼 속도를 단순히 더하는 것은 '20원+20달러=40달러'라고 계산하는 것과 다를 바 없다. 위의 식은 지구 표면에서 본 시간과 거리로 고쳐서 다시 계산해야 한다.
5. 공간이 줄어든다.
5-1. 공간도 시간과 함께 늘어나고 줄어든다
공간도 시간과 함께 늘어나고 줄어든다. 이를 이해하기 위해 다음과 같은 상황을 생각해보자. 모선에서 봤을 때 1.3광년 떨어진 행성에서 우주선이 모선으로 돌아온다고 하자. 그런데 우주선에는 1년 뒤에 폭발하는 시한 폭탄이 장치되어 있다. 시한 폭탄은 모선에서만 해체할 수 있다. 우주선은 광속의 80% 속도로 비행할 수 있다. 그러면 우주선은 모선에 돌아오지 못하고, 폭발해 버릴까? 아니면 폭발하기 전에 무사히 모선에 도착할 수 있을까?
여기에서도 핵심은 '누가 보는가?'이다. 1.3광년 떨어져 있다는 것은 모선에서 본 거리이다. 그리고 시한 폭탄이 터지는 것은 우주선에서의 1년 뒤이다. 그런데 우주선은 광속에 가까운 속도로 날아가므로, 모선에서 보면 우주선에서의 시간 흐름이 느려진다. 상대성 이론에 따르면, 모선의 1초는 모선의 0.6초이다. (왜 0.6배로 줄어드는지에 대해서는 로렌츠 수축의 공식에서 설명함) 즉, 우주선의 1년은 모선의 '1.67년(1÷0.6)'에 해당한다. 광속의 80% 속도로 1.67년 날아가면 도달 거리는 약 '1.33(1.67×0.8)'광년이 되고 폭발 전에 무사히 도착할 수 있게 된다.
5-2. 광속에 가까워질수록 공간이 줄어든다
이번에는 위의 상황을 '우주선의 입장'에서 생각해 보자. 우주선에서 보면 모선이 광속의 80% 속도로 다가오므로, 우주선에서의 1년 동안 모선이 접근하는 거리는 0.8광년(1×0.8), 모선까지의 거리는 1.3광년이므로 이렇게 되면 시간이 충분하지 않은 것처럼 생각된다. 하지만 모선 입장에서 보면 시간이 충분하기 때문에, 우주선에서 보면 시간이 충분하지 않다는 것은 모순이 된다.
그러면 어떻게 생각해야 할까? 1년 뒤에 폭발한다는 사실은 변함이 없지만, 거리가 줄어들면 폭발하기 전에 모선에 돌아올 수 있다. 실제로 특수 상대성 이론에 따라 계산하면, 모선의 1.3광년이라는 거리(공간)은 광속의 80% 속도로 날아다니는 우주선에서 0.6배로 줄어든다. 그리고 이 줄어드는 정도는 광속에 가까워질수록 커진다. (왜 0.6배로 줄어드는지에 대해서는 로렌츠 수축의 공식에서 설명함) 그러면 모선까지의 거리는 우주선에서 볼 때 0.78광년(1.3×0.6=0.78)이 된다. 즉, 1년 동안 모선이 다가오는 거리 0.8광년 보다 짧기 때문에 폭발하기 전에 모선에 도착할 수 있다.
6. 공간이 줄어드는 것도 '피장파장'
6-1. 자신 이외의 전 우주가 줄어든다.
위에서 설명한 상황에서 본 것처럼 광속에 가까운 속도로 운동하면 '공간(길이)'도 줄어든다. 광속에 가까워질수록 공간이 점점 줄어드는 것이다. 이처럼 '특수 상대성 이론'의 효과에 의해 공간이 줄어드는 것을 '로렌츠 수축(Lorentz Contraction)'이라고 부른다. 그런데 광속의 80% 속도로 날아가는 우주선에 타고 있는 관측자가 보면, 자신 이외의 우주 전체가 앞에서 뒤로 흐른다. 그래서 모선까지의 거리가 0.6배로 줄어들 뿐만 아니라, 상대성 이론의 효과에 의해 모선의 길이도 0.6배로 줄어들고, 뒤쪽의 행성도 가로 방향이 0.6배로 줄어든다. 즉, 자신 이외의 우주 전체가 0.6배로 줄어든다.
길이가 줄어드는 공식인 '로렌츠 수축의 공식'에 대해 알아보자. 빛의 속도를 c라고 하고, 어떤 물체가 정지해 있을 때의 길이를 L0라고 하면, 관측자에 대해 속도 v로 운동하고 있는 그 물체의 길이 L은 아래와 같다. 위의 예시에서 광속의 80%로 날아가는 우주선이라면, v에 0.8c를 대입해 계산하면 된다. 이 때, L=0.6L0이 나오는데, 이것이 바로 모선 입장에서 본 우주선의 길이이다. 1.3광년의 거리 또한 0.78광년(1.3×0.6)으로 줄어든다.

6-2. 공간이 줄어드는 것도 '피장파장'이다.
한편, 이 상황을 모선에서 보면 우주선만 광속의 80% 속도로 날고 있다. 그러므로 모선의 관측자가 보면 우주선의 길이만 0.6배로 줄어든다. 이처럼 등속 직선 운동을 하고 있는 관측자는 '어느 쪽이 움직이고 있는지 혹은 정지해 있는지' 알 수 없다. 따라서 시간이 느려지는 것이 '피장파장(Equality)'이었던 것과 마찬가지로, 공간(길이)가 줄어드는 것 또한 마찬가지이다. 또 시간의 느려짐과 공간의 줄어듦이 동시에 일어나는 것도 알 수 있다.
그런데 여기에서 주의할 점은 '공간(길이)'의 수축은 운동의 방향으로만 일어난다는 것이다. 속도의 방향이 가로 방향이면 세로 방향의 '공간(길이)'은 줄어들지 않는다.
7. 상대성 이론을 체험하는 입자
7-1. '특수 상대성 이론'의 효과에 의해 지상까지 도달하는 '뮤온'
앞서 설명한 우주선과 모선의 예시는 SF에서나 나옴직한 내용이지만, 상대성 이론에 따른 공간의 줄어듦을 실제로 '체험'하는 입자가 있다. 그 입자는 수백~10여 km 상공에서 발생해 지상으로 쏟아져 내리는 '뮤온(muon)'이라는 입자이다. 우주에서는 '우주선(Cosmic Ray)'이라 불리는 입자가 엄청나게 빠른 속도로 지구로 쏟아져 내린다. 우주선은 대기권에 들어오면, '대기의 분자와 충돌해서 양성자, 알파 입자, 광자, 중성자, 전자, 뮤온, 파이온, 케이온, 중성미자 등 수많은 입자들을 만들어 낸다. 이러한 입자들을 '이차우주선(Secondary Cosmic Ray)'라고 한다.
여기서는 이차우주선 중에서 뮤온을 생각해보자. 이때 뮤온은 광속에 가까운 속도로 튀어나오는데, 속도는 반응에 따라 다양하다. 그중에서도 광속의 약 99%로 날아가는 뮤온을 생각해보자. 뮤온은 본래 수명이 100만 분의 2초 정도인데, 그 이상의 시간이 지나면 붕괴해 버린다. 단순히 생각하면, 뮤온이 도달할 수 있는 거리는 '30만km×0.99×(100만 분의 2초) = 0.6km'라는 계산이 나온다. 하지만 실제로는 수백 내지 10여 km 상공에서 발생한 뮤온은 지상까지 도달한다. 이것은 광속에 가까운 속도로 날아감으로써 생기는 상대성 이론의 효과 때문이다. 지상에 있는 사람의 입장에서 생각해보면, 광속에 가까운 속도로 날고 있는 뮤온의 시간은 '특수 상대성 이론'의 효과에 의해 느려진다. 따라서 지상의 관측자가 보면, 뮤온은 수명이 늘어나 붕괴되기 전에 지상에 도달한다.
그러면 뮤온의 입장에서 보면 어떻게 될까? 뮤온의 수명은 늘어나지 않는다. 왜냐하면 시간의 빠르기는 자기 자신에게는 언제나 같기 때문이다. 실제로 뮤온의 입장에서는 공간이 줄어든다. 즉, 뮤온의 입장에서 보면, 특수 상대성 이론의 효과에 의해 지구와 대기권이 납작해지기 때문에 뮤온은 수명이 다하기 전에 지상에 도달할 수 있다.
8. 질량이 커진다.
8-1. 속도에는 넘을 수 없는 한계가 있다.
'특수 상대성 이론'은 '속도에 한계가 있다'는 놀라운 예언을 하고 있다. 즉, 어떤 기술로도 넘을 수 넘을 수 없는 속도의 한계가 있다는 것이다. 위에서 설명했던 '모선에서 출발해 날아가는 우주선'을 다시 생각해 보자. 극단적인 예로 모선이 지구에 대해 광속의 99% 속도로 날아가고 있고, 모선의 활주로에서 우주선이 모선에 대해 광속의 99%로 날아간다고 가정해 보자. 단순히 생각하면, 지구 표면에서 본 우주선의 속도는 198%(99+99)가 된다. 하지만 특수 상대성 이론에 따르면, 이때도 광속을 넘지 못하고 광속을 넘지 못하고 광속의 99.99%밖에 되지 않는다. 즉, 속도의 한계는 빛의 속도이다.
이번에는 전압을 걸어서 전자에 전기적인 에너지를 주고 가속하는 것을 생각해 보자. 일반적으로 생각하면, 계속 에너지를 가하면 전자의 속도는 무한정 커질 것이다. 하지만 속도에 한계가 있다면, 전자에 아무리 에너지를 가해도 광속에는 도달할 수 없을 것이다.
8-2. 광속에 가까워지면 물체의 질량이 커진다.
정지해 있는 전자에 에너지 E를 가해서 광속의 86.6%까지 가속했다고 하자. '특수 상대성 이론(Special Theory of Relativity)'에 따르면, 다시 똑같은 에너지 E를 추가해도 광속의 7.7%밖에 가속되지 않는다. 계속 에너지 E를 가해도, 가속량은 광속의 2.5%, 1.2%로 점차 줄어들고, 전자는 결코 광속에 도달할 수 없다.
그러면 가속에 사용되지 않는 에너지는 어디로 사라졌을까? 가속되는 양은 가하는 힘이 커질수록 커지고, 질량이 커질수록 작아진다. 위의 예에서 에너지를 가하는 것은 전자에 계속 힘을 가하는 것에 해당한다. 그렇다면 힘을 가하는데도 그다지 가속되지 않는다는 것은 '질량이 늘어나서 힘의 효과를 없애기 때문'이라고 밖에 생각할 수 없을 것 같다. 결국, '특수 상대성 이론'에 따르면, 물체는 광속에 가까워질수록 가속하기 어려워지며, 질량이 커진다는 결론이 나온다. 그리고 광속에 가까워질수록 질량은 '∞(무한대)'로 커진다.
| 총투입 에너지 | 전자의 속도 |
| 총투입 에너지 E | 전자의 속도는 광속의 86.6% |
| 총투입 에너지 2E | 전자의 속도는 광속의 94.3% |
| 총투입 에너지 3E | 전자의 속도는 광속의 96.8% |
| 총투입 에너지 4E | 전자의 속도는 광속의 98.0% |

9. 질량이란 무엇인가?
9-1. 질량이란 움직이기 어려운 정도이다.
물체를 광속에 가까울 때까지 가속하면, 질량이 커진다고 말했다. 여기서 주의할 점은, 가속한 물체의 크기가 커지는 것은 아니라는 점이다. 예컨대 100만 개의 원자로 구성되어 있는 물체를 가속해서 질량이 2배가 되었다고 하자. 이 경우, 원자의 수가 200만 개가 되는 것이 아니라, 원자 하나하나의 질량이 각각 2배가 되는 것이다.
그러면 '질량(Mass)'이란 도대체 무엇일까? 알기 쉽게 말하면 '질량이란 물체의 움직이기 어려운 정도'라고 말할 수 있다. 당구대 위에 질량이 큰 납으로 만든 공이 섞여 있다고 하자. 납으로 만든 공은 겉으로 보아 보통 당구공과 구별되지 않도록 페인트칠을 해두었다. 많은 당구공 가운데 납으로 만든 공을 손으로 집어내지 않고 찾아내려면 어떻게 해야 할까? 납으로 만든 공을 찾아내려면, '큐볼(당구에서 자기 차례의 공을 이르는 말)'로 모든 공을 맞혀 공 하나하나의 움직임을 관찰하면 된다. 큐볼로 맞히면 질량이 작은 당구공은 힘차게 굴러가지만, 질량이 큰 납으로 만든 공은 큐볼에 맞아도 조금밖에 움직이지 않는다.
9-2. 물체의 '움직이기 어려움(질량)'은 무중력 상태에서도 같다.
'질량(물체의 움직이기 어려움)'은 무중력 상태에서도 마찬가지이다. 무중력 상태에 떠 있는 당구공은 큐볼에 맞으면 힘차게 나아간다. 한편, 무중력에서도 납으로 만든 공은 큐볼에 맞으면 천천히 움직인다.
달은 지구 주위를 크게 돌고 있다. 그리고 실제로는 지구도 달과 지구의 '질량 중심(Center of mass)'을 중심으로 작게 돌고 있다. 지구가 달로부터 받는 만유인력과 달이 지구로부터 받는 만유인력의 크기는 똑같다. 하지만 질량이 큰 지구는 움직이기 어렵기 때문에, 지구는 작게 돈다. 즉, '특수 상대성 이론'에서, '광속에 가까운 속도에서 질량이 커진다'는 것은 '광속에 가까운 속도의 물체는 움직이기 어려워진다'는 의미이다.
9-3. 질량=에너지
특수 상대성 이론에 따르면, 광속에 가까운 속도의 물체에 아무리 에너지를 가해도, 속도는 그다지 증가하지 않고 질량이 증가한다. 그러면 에너지는 '속도'의 형태로 저장되지 않고, 도대체 어디로 갔을까? '에너지 보존 법칙'에 의하면 에너지의 총량은 늘어나거나 줄어들지 않는다. 이 법칙에 따르면 에너지는 사라지는 것을 허락하지 않으므로, 에너지는 어딘가에 저장되어 있을 것이다.
상대성 이론에서 이 문제에 대한 결론은 다음과 같다. 에너지는 질량으로 변했다는 것이다. 정지한 두 개의 전자 A, B에 에너지를 가해, 전자 A는 광속의 99%까지, 전자 B는 광속의 99.9%까지 가속되었다고 하자. 이 2개의 전자의 속도는 그다지 큰 차이가 없어 보인다. 하지만 이것을 충격을 100% 받아내는 벽에 부딪치게 하면, 전자 B의 충격에너지는 전자 A의 약 3.5배가 된다. 즉, 전자 B는 속도가 아닌 질량의 형태로, 전자 A보다 많은 에너지를 가지고 있는 것이다.
이와는 반대로 질량이 에너지로 바뀌는 일도 있다. 그 예로 원자력 발전소에서 일어나는 '우라늄(U, 원자번호 92번 원소)'의 핵분열 반응이 있다. '핵분열 반응(nuclear fission reaction)'에서는 질량이 열에너지로 바뀐다. 발전소에서는 이 열에너지가 물을 끓이고, 거기에서 발생하는 수증기로 터빈을 돌려 전기 에너지를 만든다. 우라늄의 원자핵은 분열해서 작은 원자핵으로 쪼개지기 쉬운 성질을 가지고 있다. 그런데 우라늄이 분열해서 만들어진 질량을 모두 합쳐도 원래 우라늄의 질량보다 0.1% 정도 부족하다. 아주 적기는 하지만, 이 질량의 감소분이 열에너지를 거쳐 우리 일상에서 사용되는 전기에너지가 되는 것이다.
9-4. 작은 질량이라도도 엄청난 에너지를 가지고 있다.
결론적으로, 에너지는 질량으로 변할 수 있고, 질량은 에너지로 변할 수 있다. 즉, 질량과 에너지는 같은 것이다. 이 관계를 수식으로 나타낸 것이 '특수 상대성 이론'의 유명한 공식 E=mc2이다. (E=에너지, m=질량, c=광속) 과학의 역사에서 오랜 세월 동안 질량과 에너지는 각각 다른 것으로 취급받았다. 그 때문에 좌변의 에너지 E의 단위 '줄(J)'과 우변의 질량 m의 단위 'kg'은 전혀 다르다. 하지만 E=mc2 공식 중의 c2은 역사적으로 별개의 것으로 취급되어 온 에너지 E와 질량 m을 연결하는 다리 역할을 하게 되었다. 이 c2는 이론적인 계산으로 이끌어낸 것이지만, 여기에서도 광속 c가 등장하는 것을 보면 광속 c가 우주의 법칙과 밀접하게 관련된 아주 중요한 수라는 것을 알 수 있다.
구체적으로 계산 사례를 들어 보자. 우라늄의 핵분열 반응에 의해, '10g(0.01kg)'의 질량이 에너지로 바뀌는 경우를 생각해 보자. E=mc2이므로, E=0.01×(30만×1000)2'를 계산하여, 900조 J이 된다. 이처럼 매우 작은 질량이라도 엄청난 질량을 가지고 있다. (참고로 이 계산에서 30만에 1000을 곱한 이유는 단위를 km에서 m로 바꾸기 위함이다. 1J은 질량 1kg의 물체를 1m 움직이는데 필요한 에너지이기 때문에, m로 단위를 바꾼 다음에 계산해야 한다.)