빛의 속도는 어떻게 측정했을까?

0. 목차

1. 빛의 속력은 초속 약 30만 km
2. 갈릴레이가 생각한 광속 측정법
3. '올라우스 뢰메르'의 광속 측정법
4. '아르망 피조'의 광속 측정법
5. 이론적으로 광속이 유도되다.
6. '레온 푸코'의 회전 거울을 사용한 광속 측정법
7. 광속 측정의 정밀도가 점점 더 정확해졌다.
8. 광속의 값은 측정값에서 정의값으로 바뀌었다.

반응형

1. 빛의 속력은 초속 약 30만 km

 어두운 방 안에서 전등 스위치를 켜면, 순식간에 방 안이 밝아진다. 하지만 전구가 밝아진 것과 동시에 방이 밝아진 것은 아니다. 전구에서 나온 빛은 어느 정도의 시간이 지난 후에야 방의 구석까지 도달한다. 다만, 빛의 속력은 우리의 일상적인 감각과 비교하면 상상을 초월할 정도로 빠르기 때문에, 전등 스위치를 켠 순간에 방이 밝아진 것처럼 보이는 것이다.

 그러면 빛이 나아가는 속력은 어느 정도일까? 빛은 1초에 297924.58km나 나아간다. 결국 빛의 '속력(거리÷시간)'은 초속 약 30만 km이다. 아폴로 우주선은 지구로부터 약 38만 km 떨어져 있는 달에 도착하는 데 약 3일이 걸렸다. 하지만 빛은 약 1.3초 만에 도달할 수 있을 정도의 엄청난 속력이다. 빛과 자주 비교되는 것 중에는 '소리(Sound)'가 있다. 소리가 공기 속을 나아가는 속력은 약 340m이다. 우리는 누군가가 말을 하고 나서 그 소리가 느낄 때까지 시간차를 거의 느끼지 못한다. 초속 340m의 소리마저 그런데, 소리의 90만 배에 가까운 속력을 가진 빛이 나아가는 모습을 실감하지 못하는 것은 너무나도 당연한 일이다.

반응형

2. 갈릴레이가 생각한 광속 측정법

 몇백 년 전까지만 해도 인류는 빛의 속력이 무한대라고 생각했다. 즉, 아무리 떨어져 있어도 빛은 순간적으로 도달한다고 생각했다. 그러면 사람들은 빛의 속력이 유한하다는 사실을 어떻게 알게 되었을까? 빛의 속력이 무한대가 아니라 유한하다고 최초로 지적한 사람은 이탈리아의 과학자 '갈릴레오 갈릴레이(Galileo Galilei, 1564~1642)'였다.

 갈릴레이는 멀리 떨어진 두 곳에 있는 사람이 등불의 빛을 이용해 신호를 주고받음으로써, 빛의 속력을 구할 수 있다고 생각했다. 예컨대 5km 떨어진 장소에서 두 사람이 빛의 신호를 왕복시키면, 빛은 10km 나아간다. 그리고 이 왕복하는 데 걸린 시간이 1초라고 하면, 빛의 속력은 초속 10km라는 것이다. 우선 몇 km 떨어진 두 지점에 A씨와 B씨가 서 있다. 우선 A씨가 가지고 있는 등불의 덮개를 벗겨서 B씨에게 빛의 신호를 보낸다. A씨의 등불이 보이면, B씨는 즉시 자신이 가진 등불의 덮개를 벗겨서 A씨에게 빛의 신호를 되돌려 보낸다. 'A씨가 빛의 신호를 보내고 나서 B씨가 되돌려 보낸 빛의 신호가 A씨에게 다다르기까지 걸린 시간'이 '빛의 두 지점을 왕복하는데 걸린 시간'이다.

 광속을 측정하는 방법 자체가 틀린 것은 아니었지만, 갈릴레이는 이 방법으로 광속을 측정할 수 없었다. 왜냐하면 5km 거리를 왕복하는 데, 빛은 거의 0.00003초밖에 걸리지 않기 때문이다. 당시에는 이처럼 짧은 시간을 정확하게 측정하는 정밀한 시계가 없어서, 갈릴레이가 살았던 시대에는 이 방법으로 광속을 측정할 수 없었다.

3. '올라우스 뢰메르'의 광속 측정법

 그러면 어떻게 해야 빛의 속력을 측정할 수 있을까? 이 질문에 최초로 답한 사람은 덴마크의 천문학자 '올라우스 뢰메르(Olus Roemer, 1644~1710)'이다. '올라우스 뢰메르'는 목성의 위성 '이오(Io)'가 목성의 그림자에 가려지는 시간의 간격이 변하는 현상을 이용해서, 광속의 값을 구하는 데 성공했다.

 지구와 목성은 태양 주위를 공전하기 때문에, 시간의 흐름에 따라 지구와 목성의 위치 관계는 계속 변한다. 예컨대, 지구가 A의 위치에 있다가 B의 위치로 이동하면 지구와 목성은 가까워진다. (아래의 그림에서 시각 B는 목성과 가장 가까워지는 시각이다.)

지구, 목성, 이오

3-1. 광속은 유한하다.

 이오는 목성 주위를 약 42.5시간 한 바퀴 돈다. 따라서 만약 광속이 무한대라면, 지구나 목성이 어떤 위치에 있어도 이오가 목성의 그림자에 가려지는 순간은 42.5시간마다 관측되어야 한다. 예컨대, 1월 1일 0시에 이오가 목성의 그림자에 가려지는 이오의 '식(eclipse)'이 일어났다고 하자. 단순히 생각하면, 다음에 이오의 식이 일어나는 시각은 42.5시간 후인 1월 2일 18시 30분이다. 그리고 그다음에 이오의 식이 일어나느 시각은 다시 42.5시간 후인 1월 4일 13시여야 한다. 그 후의 관측 예정 시각도 단순히 42.5시간을 더해감으로써 계산할 수 있다. 만약 광속이 무한대라면, 이 관측 예정 시각대로 이오의 식이 관측될 것이다.

 하지만, 실제로는 광속은 유한한 데다가, 목성·이오·지구 사이의 거리는 계속 변한다. 그래서 이오의 식이 일어나는 시간은 '단순한 관측 예정 시각'에서 조금씩 어긋난다. 지구와 목성·이오 사이의 거리는 시각 A보다 시각 B일 때 짧아진다. 따라서 B에 있을 때 목성·이오에서 오는 빛은, A에 있을 때 목성·이오에서 오는 빛보다 빨리 지구에 도착한다. 뢰메르는 이오와 지구의 거리가 어느 정도 짧아지면, 이오의 '식'의 순간이 '관측 예정 시각보다 어느정도 빨리 관측될지'를 산출해 광속의 값을 구했다. 상세한 계산 방법은 아래에서 소개한다.

3-2. 측정된 광속의 값은 실제 값보다 30% 정도 작았다.

 시각 A의 위치에서 시각 B의 위치로 이동할수록, 지구와 목성·이오 사이의 거리는 점점 짧아진다. 그러면 이오의 식은 그전의 관측 시각보다 42.5시간 후라는 '단순한 관측 예정 시각'보다 빨리 관측된다. 반면 시각 B일 때, 지구는 목성·이오와 가장 가까워지기 때문에, 시각 B 이후에 지구는 목성·이오가 조금씩 멀어진다. 그래서 시각 B 이후, 이오의 식은 그전의 관측 시각보다 42.5시간 후라는 '단순한 관측 예정 시각'보다 늦게 관측된다.

 이오의 식이 예정 시각보다 가장 빨리 관측되는 때는 시각 B처럼 지구와 목성·이오가 최단거리에 있을 때다. 반대로 예정 시각보다 가장 늦게 관측되는 것은 지구와 이오가 최장거리에 있을 때다. 뢰메르는 관측을 통해, 가장 빨리 관측될 때와 가장 늦게 관측될 때, 관측 시각에 22분의 차이가 있음을 알아냈다. 이 22분이라는 시간은 '지구와 이오의 최단거리와 최장거리의 차'를 말한다. 즉, '지구 공전 궤도의 지름(약 3억km)'을 빛이 나아가는 데 걸리는 시간을 말한다.

 뢰메르는 이 사실에 주목해 빛의 속력을 계산했다. 이렇게 해서 뢰메르가 1676년에 계산한 빛의 속력은 초속 21.4만 km였다. 이는 현재 알려져 있는 광속의 값보다 30% 정도 낮은 값이지만, 이것은 당시의 시계나 천체 관측의 정밀도가 낮아서 생기는 오차이다. 어쨌든, 인류는 처음으로 광속의 값을 과학적으로 구하는 데 성공하였다.

반응형

4. '아르망 피조'의 광속 측정법

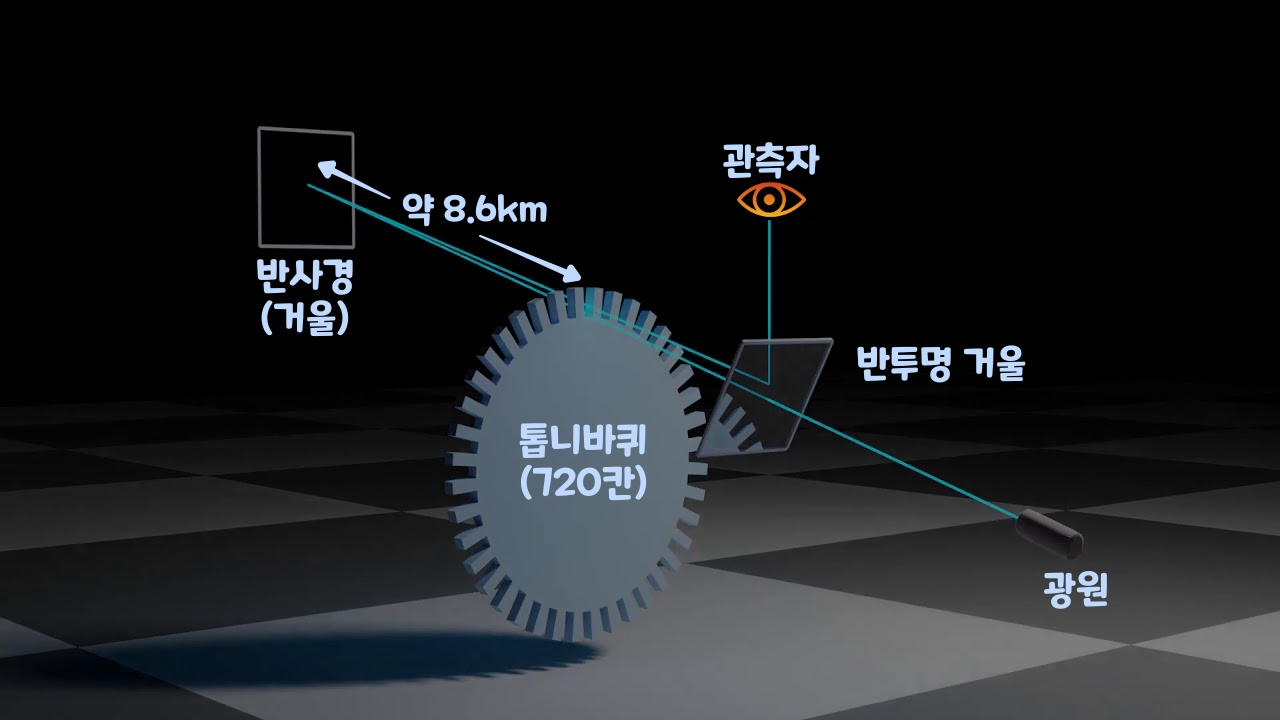
 천문 현상을 이용하지 않고, 실험 장치만으로 광속을 측정하는데 최초로 성공한 사람은, 프랑스의 물리학자 '아르망 피조(Armand Hippolyte Louis Fizeau, 1819~1896)'이다. 피조의 '광속 측정 장치'는 멀리 떨어진 두 점 사이를 빛이 왕복할 때 걸린 시간을 재는 것으로, 기본적으로는 '갈릴레이'의 광속 측정 아이디어와 같다. 피조는 망원경 같은 관측 장치와, 빛을 반사시키는 장치를 마련하여 그 사이를 빛이 왕복하도록 했다. 그 거리는 편도 약 8.6km이며, 왕복으로는 17.2km이다. 17.2km라는 거리는 사람에게는 충분히 먼 거리이지만, 빛의 속도로는 0.0001초도 걸리지 않는 거리이다. 당시 기술로는 이 짧은 시간을 정확하게 측정하기가 어려웠다. 그래서 피조는 회전하는 톱니바퀴를 사용해, 빛이 왕복하는 데 걸린 시간을 구했다.

 피조는 둘레에 720개의 톱니가 달린 톱니바퀴를 빛이 지나가는 길에 놓고, 고속으로 회전시켰다. 그러면 톱니바퀴는 톱니의 빛을 막거나 통과하기를 고속으로 반복한다. 톱니와 톱니 사이를 지나온 빛은 8.6km 앞의 장치에서 반사되어 되돌아온다. 피조는 1초 사이에 12.6회전의 빠르기로 톱니바퀴를 회전시키면, 반사되어 되돌아온 빛이 1개만큼 돌아간 톱니에 의해 정확히 차단된다는 사실을 발견했다. 되돌아온 빛이 톱니에 차단된다는 사실은 망원경으로 관측하면 빛이 어두워지므로 알 수 있다.

 이것은 톱니바퀴의 톱니가 1개 돌아가는 사이에 빛이 왕복 17.2m를 진행해왔다는 사실을 뜻한다. 톱니가 1개만큼 돌아가는 시간을 계산하면, 약 '0.000055초(=1초÷12.6회전÷720개÷2)'임을 알 수 있다. 결국 빛은 17.2km의 거리를 0.000055초 동안 나아갔다는 것이다. 이리하여, 1849년에 피조가 측정한 광속의 값은 약 '31.3만km(=17.2km÷0.000055초)'였다.

 톱니가 1개만큼 돌아가는 데 걸리는 시간은 '1초 ÷ 1초당 톱니바퀴의 회전수 ÷ 톱니의 수 ÷ 2'로 구해진다. 톱니바퀴의 톱니가 1개만큼 돌아간다는 것은 톱니가 바로 옆의 '빈틈(톱니와 톱니 사이)'까지 이동함을 뜻한다. 따라서 마지막에 2로 나누지 않으면, 바로 옆의 '빈틈'까지가 아니라, 바로 옆의 '톱니'까지 돌아가는 데 걸리는 시간을 구하는 결과가 된다.

피조의 '광속 측정 장치'

5. 이론적으로 광속이 유도되다.

 피조 이후에 실시된 여러 광속 측정 실험에 의해, 빛의 속력은 정밀도가 높게 구해져 광속은 약 30만 km라는 사실이 알려졌다. 하지만 빛의 정체가 과연 무엇인지, 그리고 빛이 공간에서 어떻게 전해지는지는 전혀 알 수가 없었다. 그렇게 빛의 정체가 미스터리로 남아 있던 그때, 빛과 관계없는 것처럼 보이는 연구를 통해 이에 대한 답을 한 사람이 있다. 바로 영국의 물리학자 '제임스 클러크맥스웰(James Clerk Maxwell, 1831~1879)'이다.

5-1. 맥스웰의 전기와 자기 연구

맥스웰은 전기와 자기에 관 한 수많은 실험 결과를 종합적으로 설명할 수 있는 이론의 완성을 목표로 하고 있었다. 그리고 마침내 전기와 자기의 움직임을 설명하는 물리학 이론인 '전자기학(electromagnetics)'을 완성했다. '전자기학'은 그때까지 별개의 것으로 생각되었던 '전기(Electricity)'와 '자기(Magnetism)'가 서로 영향을 미친다는 사실을 밝혔다.

자석의 주위에는 그 자기력이 미치는 범위인 '자기력'이 존재한다. 마찬가지로 전기의 주위에는 '전기장'이라는 범위가 존재한다. 도선에 전류가 흐르면 도선 주위의 공간에 '자기장'이 발생하고, 도선 가까이 놓인 방위 자석이 그 영향을 받아 움직인다. 또 자석을 코일에 가까이 대면 자석 주위의 공간에 '전기장(Electric Field)'이 발생하고, 그 영향으로 코일에 전류가 흐른다. 이처럼 '전기'는 '자기'를 만들어 내고, '자기'는 '전기'를 만들어 낸다.

5-2. 빛은 전자기파였다.

교류 전류처럼 방향이 변하면서 전류가 흐르면, 주위에는 전류가 감기듯이 '자기장(Magnetic Field)'이 발생한다. 그러면 그다음에는 그 자기장에 감기듯이 '전기장(Electric Field)'이 발생한다. 다시 이 전기장에 자기장이 생기고, 이 자기장에 다시 전기장이 생긴다. 이런 식으로 전기장과 자기장이 연쇄적으로 생긴다. 그 결과, 전기장과 자기장의 연쇄는 파동처럼 나아가게 된다. 맥스웰은 이 파동을 '전자기파(electromagnetic wave)'라고 불렀다.

맥스웰은 전자기파가 나아가는 속력을, 직접 재지 않고 이론적인 계산에 의해 구했다. 그 결과, 그 값은 초속 약 30만 km가 되었다. 신기하게도 당시 밝혀져 있던 광속의 값과 일치했다. 이런 사실로부터 맥스웰은 전자기파와 빛이 같은 것이라고 결론을 지었다. 이로써 광속이 유한하다고 지적한 갈릴레이 이후, 2세기 이상이 지나서야 '빛의 속력'과 '빛의 전달 메커니즘'이 밝혀지게 되었다.

 진공 중의 '전자기파의 속력(V)'는 파동의 속력을 직접 조사하지 않아도, '진공의 투자율(µ0)'과 '진공의 유전율(ε0)'이라는 2개의 값으로 구할 수 있다. '전자기파의 속력(V)'는 (µ₀×ε₀)^-0.5으로 구한다. µ₀의 값은 약 1.26×10^-6N/A²이고, ε₀의 값은 약 8.85×10^-12N/V²이다. N(뉴턴)'은 힘의 단위이다.

전자기파(Electromagnetic Wave)

6. '레온 푸코'의 회전 거울을 사용한 광속 측정법

 프랑스의 물리학자 '레온 푸코(Leon Foucault, 1819~1868)'는 회전 거울을 사용하여 광속을 측정했다. 광원에서 나온 빛은 '반거울(빛의 일부만 통과시키고 일부는 반사시키는 거울)'과 렌즈를 통해 회전 거울에 도달한다. 회전 거울에서 반사한 빛이 오목 거울에서 반사하고, 다시 회전 거울로 돌아왔을 때 회전 거울의 각도는 미세하게 어긋나게 된다. 그러면 회전 거울에서 반거울로 돌아오는 위치가, 거울이 회전하지 않는 경우(노란색)에 비해 회전만큼 어긋난다(보라색). 회전 거울의 회전 속도, 회전 거울과 오목 거울의 거리, 그리고 관측면에서 생기는 반사광의 어긋남으로부터 광속을 구할 수 있다.

'레온 푸코'의 회전 거울을 사용한 광속 측정법

7. 광속 측정의 정밀도가 점점 더 정확해졌다.

7-1. 광학적 측정

 1849년에 피조가 지상에서 '광속 측정 실험'에 성공하고 나서, 광속의 측정법과 그 측정 정밀도가 조금씩 더 정확해졌다. 피조의 광속 측정법은 일정한 거리를 왕복시키고, 그 이동에 걸리 시간으로부터 광속을 구하는 방법이었다. 이러한 방법을 '광학적 측정'이라고 한다. 피조는 빛의 왕복에 걸린 시간을 측정하기 위해 회전하는 톱니바퀴를 사용하였다. 피조 이후, 과학자들은 톱니바퀴 되신에 회전하는 거울을 사용하거나 '카셀(Carsel)'이라 불리는 빛의 강도를 변화시키는 장치를 사용하면서 측정법을 연구하였고, 그 결과 정밀도를 높일 수 있었다. 피조가 구한 광속은 초속 31.3만km으로 실제보다 4% 이상 큰 값이었으나, 세월이 가면서 측정 오차와 실제값의 차이는 점점 작아졌다.

 아래의 표는 '광학적 방법에 의한 광속 측정'의 역사를 연표로 정리한 것이다. (현재 알려져 있는 광속의 값은 초속 29만 9792.458km)

측정 연도	측정자	사용 장치	측정값(1000km/s)
1849	피조	회전 톱니바퀴	313
1862	푸코	회전 거울	198.0±0.5
1872	코르뉴	회전 톱니바퀴	198.5±0.9
1874	코르뉴	회전 거울	300.4±0.8
1878	마이컬슨	회전 거울	300.14±0.70
1879	마이컬슨	회전 거울	299.91±0.05
1882	뉴컴	회전 거울	299.81±0.03
1882	마이컬슨	회전 거울	299.85±0.06
1908	페로탱(Perrotin), 프림(Prim)	회전 톱니바퀴	299.70±0.08
1924	마이컬슨	다면경	299.802±0.030
1926	마이컬슨	다면경	299.796±0.004
1928	카롤루스, 미텔슈테트	카셀	299.778±0.020
1935	마이컬슨, 피스, 피어슨	다면경	299.774±0.011
1937	앤더슨	카셀	299.771±0.012
1941	앤더슨	카셀	299.776±0.014

7-2. 전파 기술을 이용한 광속 측정

 하지만 광학적인 방법으로는 측정의 정밀도에 한계가 있었다. 빛이 나아가는 긴 거리를 정밀하게 측정하기도 어렵고, 기압이나 기온에 따라 변하는 공기의 굴절률의 영향을 고려할 필요도 있었기 때문이다. 그래서 더욱 정밀한 광속 측정법으로, 1950년대 무렵부터는 전파를 사용해 광속이 측정되었다. 전파는 가시광선과 같은 전자기파의 일종이기 때문에, 전파도 광속으로 나아간다. 그런데 전자기파에서는 '속력=파장×주파수(진동수)'라는 공식이 성립한다. 따라서 빛이 나아간 거리와 이동에 걸린 시간 대신 이 관계식을 사용해, 전파의 파장과 주파수로부터 광속의 값을 구할 수 있다.

 전파로 광속이 정밀하게 측정된다는 사실이 알려지자, 광학적인 광속 측정법이 진화한 것처럼 전파 기술을 이용한 광속 측정법도 진화해 왔다. 아래의 표는 '전파 기술을 이용한 광속 측정'의 역사를 연표로 정리한 것이다.

측정 연도	측정자	사용 장치	측정값(1000km/s)
1948	에센(Louis Essen) 등	고정 장공진기	299792±4.5
1949	애슬랙슨(Aslakson)	레이더	299792.4±3.6
1950	에센	가변 장공진기	299792.5±1.5
1950	한센(Hansen), 볼(Bol)	고정 장공진기	299789.3±1.0
1951	애슬랙슨	레이더	299794.2±2.8
1952	프룸(Keith Davy Froome)	마이크로파 간섭계	299792.6±0.7
1954	프룸	마이크로파 간섭계	299792.75±0.30
1955	플라이머(Ian Plimer)등	적외 회전 스펙트럼	299792±6
1955	플로먼(Florman)	전파 간섭계	299795±1.5
1958	프룸	마이크로파 간섭계	299792.50±0.10
1950~1962	베르그스트란드(Bergstrand) 등	지오디미터	299792.6±0.25
1965	콜리바예프(Kolibayev)	지오디미터	299792.6±0.06
1967	그로세(Grosse)	지오디미터	299792.5±0.05
1967	짐킨(G. S. Simkin)	마이크로파 간섭계	299792.56±0.11
1969	카롤루스 등	초음파 변조	299792.47±0.15

8. 광속의 값은 측정값에서 정의값으로 바뀌었다.

 이후에는 진행 방향이나 파장이 가지런하게 모아진 빛인 '레이저광(laser light)'을 사용함으로써 더욱 정밀하게 광속의 값을 측정할 수 있게 되었다. 그리고 1970년대에는 광속의 값이 초속 29만 9792.458km가 거의 틀림없다는 사실이 밝혀졌다. 그리고 1983년에는 단위를 결정하는 국제회의에서 광속은 '초속 29만 9792.458km'로 정의되었다. 이로써 광속은 측정값이 아니라 정의값이 되었다.