'무한(∞)'은 '끝이 없다'는 개념으로, '무한'의 세계를 머릿속에 떠올리는 일은 쉽지 않다. 그래서 무한에 관한 '역설(Paradox)'도 많이 만들어졌다. '무한'과 관련된 역설에는 어떤 것들이 있을까?
0. 목차
- 무한 호텔의 역설
- 제논의 역설
- 갈릴레이의 역설
- 톰슨의 램프
- 2=1의 증명?
1. 무한 호텔의 역설
독일의 수학자 '다비트 힐베르트(David Hilbert, 1862~1943)'는 무한 객실이 있는 '무한 호텔(infinite hotel)'이라는 기묘한 '패러독스(paradox)'를 생각했다. 무한의 개념을 이해하는데 도움이 되는 사고 실험이다.

1-1. 무한의 손님이 찾아왔다.
무한 호텔에 '무한(∞)'의 손님이 숙박하고 있어 방이 꽉 차 있던 어느 날, 손님 한 명이 찾아왔다. 그 손님은 머물 호텔이 없으니 어떻게든 이 호텔에 묵고 싶다고 한다. 이에 호텔 지배인은 숙박객 전원을 자신의 방 번호 보다 하나 큰 방 번호의 방으로 옮기도록 조치했다. 1호실의 손님은 2호실로, 2호실의 손님은 3호실로, 3호실의 손님은 4호실로... 이러한 방법으로 호텔의 1호실을 비울 수 있었고, 새로 찾아온 손님은 1호실에서 묵을 수 있었다.

1-2. 무한의 손님이 또 찾아았다.
그런데 이 날, 무한의 손님이 또 찾아왔다. 이미 무한의 손님이 숙박하고 있는데 무한의 손님을 어떻게 더 받는단 말인가? 하지만 호텔 지배인은 숙박객 전원을 자신이 숙박하고 있던 방 번호의 2배수의 번호의 방으로 옮기도록 하여 손님들을 받을 수 있었다. 1호실 손님은 2호실로, 2호실 손님은 4호실로, 3호실 손님은 6호실로...
말이 안되는 것 같지만, 사실 이 논리는 수학적으로 올바르다. 이는 무한이 가지고 있는 직관에 반하는 성질 때문에 생긴 '패러독스(paraedox)'이다. 유한의 세계에서는 예를 들어 1부터 10까지 등장하는 짝수의 수(5개)는 1부터 10까지 등장하는 자연수의 수(10개) 보다 당연히 적다. 하지만 무한의 세계에서는 짝수 전체가 자연수 전체가 1대 1로 대응해 그 크기가 같아진다. 무한의 세계에서는 부분 집합이 집합 전체와 같은 크기가 되는 신비한 성질이 나타날 수 있다는 것이다.

1-3. 무한의 버스가 '무한'대 찾아왔다.
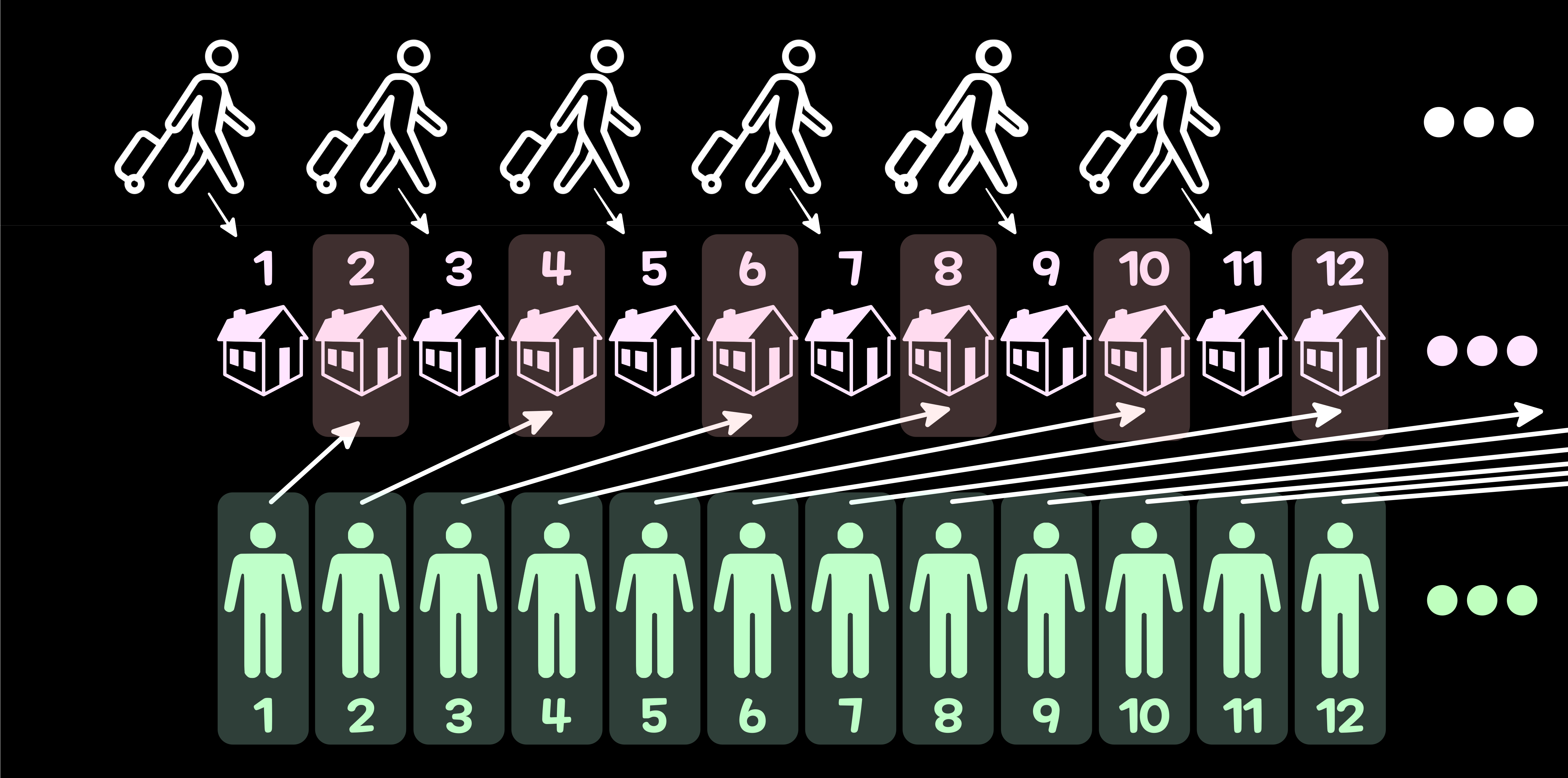
이번에는 무한 호텔에 '무한의 버스'가 '무한(∞)' 대 찾아왔다. 이전에 호텔 지배인은 2배수의 방 번호로 숙박객 전원을 이동시켜 빈방을 만들어 새로운 손님들을 숙박시킬 수 있었다. 하지만 이번에는 무한대의 손님이 무한대로 있다. 이전의 방식을 무한 반복하면 이번에도 손님들을 숙박시킬 수는 있다. 하지만 숙박객의 방을 무한이 변동시키면 이 작업은 영원히 끝나지 않을 것이다. 그러면 어떻게 해야 숙박객들을 한 번만 이동시키고 새로운 손님들을 모두 받을 수 있을까?
단 한 번만 숙박객들을 이동시키고 새로운 손님들을 모두 받을 수 있는 방법이 존재한다. 그러한 방법 중에 하나는 '소수'를 이용하는 것이다. '소수(prime number)'란 '1과 자기 자신만으로 나누어 떨어지는 1보다 큰 양의 정수'를 말한다. 이 소수는 끝없이 무한히 존재한다고 이미 증명되어 있다. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 등이 '소수'이다.
먼저 숙박객들을 2배수의 방 번호로 숙박객을 전원 이동시켜 홀수의 방을 비운다. 먼저 첫 번째의 무한 버스 손님들을 3n(n=1, 2, 3, 4...) 호실로 안내한다. 그러면 첫 번째 무한 버스의 손님들은 3, 9, 27, 81... 호실에 투숙하게 된다. 두 번째의 무한 버스 손님들은 5n(n=1, 2, 3, 4...)호실로 안내한다. 그러면 두 번째 무한 버스의 손님들은 5, 25, 125, 625... 호실에 투숙하게 된다. 세 번째의 무한 버스 손님들은 7n(n=1, 2, 3, 4...)호실로 안내한다. 그러면 세 번째 무한 버스의 손님들은 7, 49, 343, 2401... 호실에 투숙하게 된다. 마찬가지로 p 번째 무한 버스의 손님들은 pn(n=1, 2, 3, 4...)호실로 안내하면 된다. 첫 번째 무한 버스의 손님들을 두 번째 소수인 3부터 할당한 이유는 2는 짝수이기 때문에 사용할 수가 없기 때문이다. 이런 식으로 손님의 방을 배정하면 방이 중복되는 일이 없어, 기존의 숙박객들을 한 번만 이동시키고 모든 손님들의 방을 다 배정시킬 수 있다.
2. 제논의 역설
고대 그리스의 철학자 '아리스토텔레스(기원전 384~기원전 332)'는 그의 저서 '자연학'에서 몇 개의 역설을 소개했다. 이 역설들은 원래 기원전 철학자인 '엘레아의 제논(그리스어: Ζήνων ὁ Ἐλεάτης, 기원전 490년경~기원전 430년경)'이 언급했던 것으로 '제논의 역설(Zeno's Paradox)'이라고도 한다. '제논의 역설'은 사물이 움직이고 있다고 우리가 느끼는 모든 것들은 환상이라는 '파르메니데스(Παρμενίδης, 기원전 510년 경~기원전 450년 경)'의 사상을 지지하기 위해 만든 것이다.

2-1. 아킬레우스와 거북의 역설
첫 번째로 소개할 '제논의 역설'은 '아킬레우스와 거북이의 역설(Achilles and the Tortoise Paradox)'이다. '아킬레우스와 거북이의 역설(Achilles and the tortoise paradox)'은 제논의 역설 중에서 가장 유명하다. 원래 '아킬레스와 거북'은 제논이 피타고라스의 '정수론(Number Theory)'을 공격하기 위한 논제였다. 물론 피타고라스 학파는, 제논의 주장이 정신나간 헛소리라는 것을 알았음에도 이에 논리적으로 대응하지 못했었는데, 이는 당시에 '무한(infinite)', '극한(limit)'의 개념이 없었기 때문이었다. 무한, 극한의 개념은 19세기가 되서야 정립되었다.
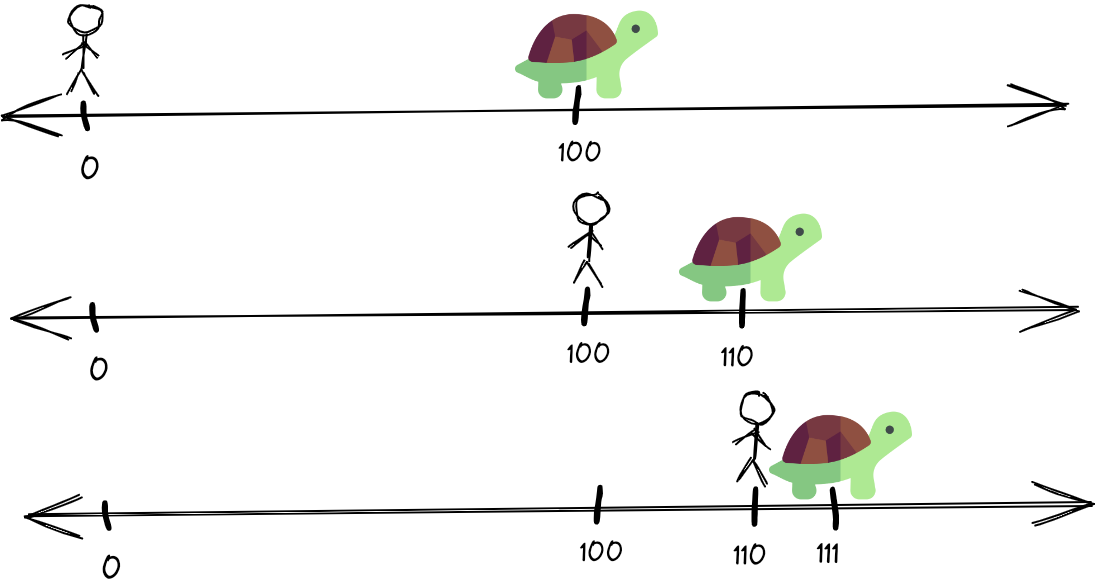
'아킬레스와 거북'의 내용은 다음과 같다. 제논은 다음의 상황에서, 발이 아무리 빠른 '아킬레스(Achilles)'라도 '거북(Tortoise)'을 영원히 따라잡을 수 없다고 주장했다. 아킬레스의 100m 앞에 거북이 있고, 아킬레스는 거북을 향해 달려간다. 아킬레스는 10초에 100m를 달릴 수 있고, 거북은 10초에 10m를 도망갈 수 있다고 가정하자. 그러면 10초 후에는 아킬레스는 거북이 있던 100m 지점에 가 있을 것이고 거북은 10m 더 나아가 거북은 아킬레스의 10m 앞에 있게 된다. 다음 또 1초 후에는 아킬레스는 거북이 있던 지점에 가있을 것이고 거북은 1m 더 앞으로 나아가 있을 것이다. 다음 또 0.1초 후에는 거북에 있던 지금에 가 있을 것이고 거북은 0.1m 더 앞으로 나아가 있을 것이다. 이런 식으로 아킬레스가 아무리 거북을 쫓아가도 아킬레스는 거북을 따라잡을 수 없게 된다는 것이 제논의 주장이다.
하지만 계산해보면 10 + 1 + 0.1 + 0.01 + 0.001 + 0.0001... = 11.11111...이므로, 아킬레스가 달리는 시간은 '9 분의 1000초 (11.11111... 초)'에 수렴한다는 것을 알 수 있다. 즉, 아킬레스는 11초가 약간 지나서 거북을 따라잡을 수 있다. 그러면 제논은 무엇을 잘못 생각했을까? 제논은 무한 개를 수를 더하면 무한대가 될 것이라는 착각을 하고 있었던 것이다. 제논은 '무한등비급수(일정 비율로 줄어드는 수)'는 아무리 더해도 유한하다는 사실을 이해하지 못했다.
2-2. 이분법의 역설
두 번째로 소개할 '제논의 역설'은 '날아가는 '이분법의 역설(Dichotomy Paradox)'이다. '아킬레스와 거북'을 다른 예로 바꿔놓은 것이라고 보면 되는데, 내용은 다음과 같다.
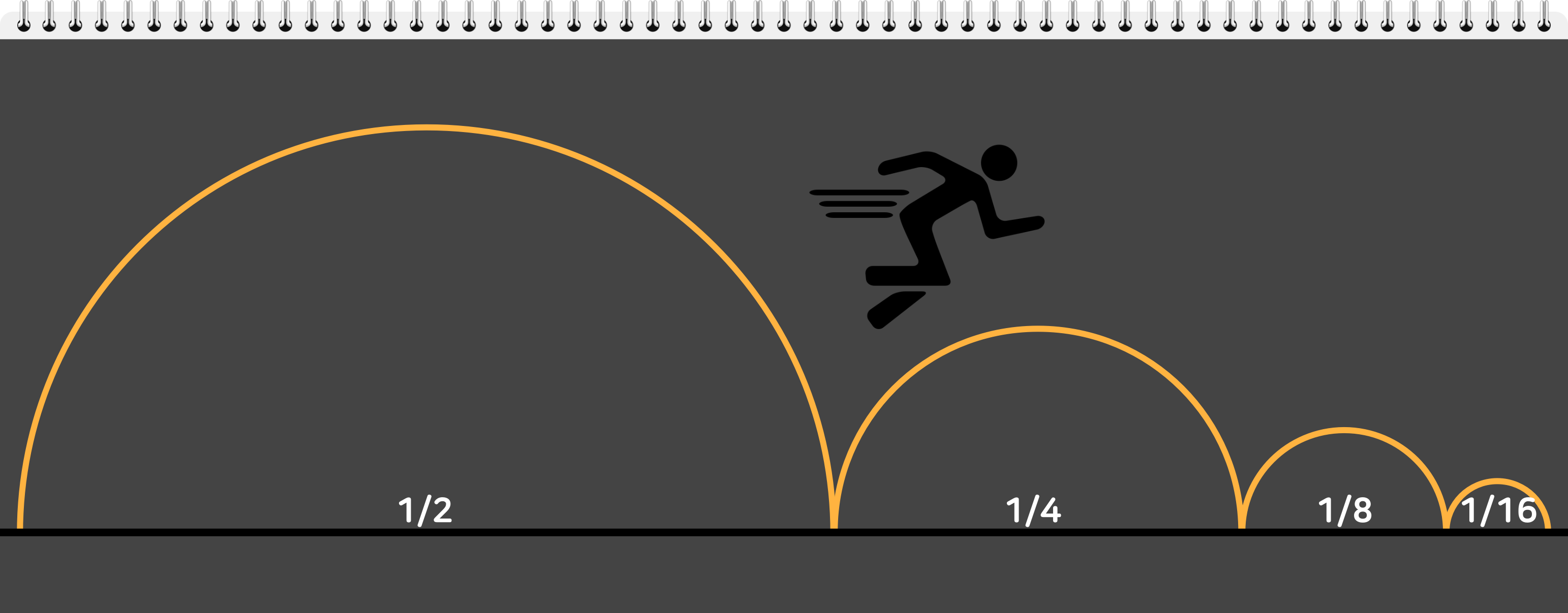
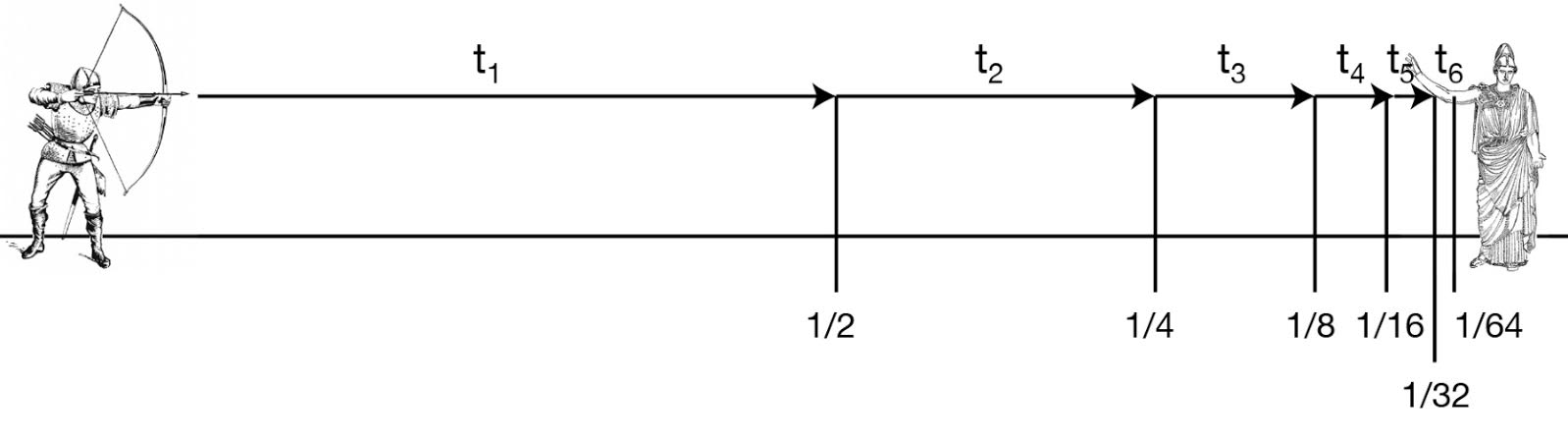
어떤 사람이 목적지에 도달하기 위해서는 중간 지점을 통과해야 한다. 중간 지점까지 간다 해도 다시 사람과 목적지 사이에 중간 지점이 설정될 수 있으며, 또 그 지점까지 간다고 해도 사람과 목적지 사이에 중간 지점이 설정될 수 있다. 이러한 논리로 제논은 무한의 시간이 지나도 목적지에 도달하는 것이 불가능하다는 주장을 했다. 남은 거리는 한없이 0에 가까워지겠지만 결코 0은 되지 않는다는 것이다. 하지만 극한의 개념이 정립된 지금은 1/2 + 1/4 + 1/8 + 1/16 + 1/32... = 1 이므로 계산의 결과가 무한대가 아니라는 사실을 쉽게 알 수 있다. 이 또한 무한의 덧셈이 '∞(무한대)'가 된다는 오해에서 생긴 잘못된 주장이다.
2-3. 화살의 패러독스
세 번째로 소개할 '제논의 역설'은 '날아가는 '화살의 패러독스(Arrow Paradox)'이다. 제논은 '날아가는 화살은 순간순간 정지해 있다. 따라서 정지해 있는 화살은 제아무리 모아도 화살은 날아가지 않는다.'라는 황당한 주장을 했다. 화살이 날아간다는 운동 자체를 부정해버리는 정신 나간 소리를 한 것이다. 하지만 화살은 분명히 날아갈 수 있기 때문에 이러한 주장에는 결함이 있는 것이 확실하다. 이 주장은 무엇이 잘못되었을까?
날아가는 화살을 카메라로 촬영하면 그 사진은 한순간을 잘라낸 것처럼 보일 것이다. 하지만 셔터의 속도를 느리게 하면 화살이 날아가고 있음을 알 수 있다. 결국 우리가 포착한 '한순간'은 실제로 어느 정도의 시간이 있는 것이다. 그러면 이번에는 반대로 셔터의 속도가 아주 빠른 카메라로 날아가는 화살을 찍어보자. 그러면 화살은 마치 정지한 것처럼 보일 것이다. 하지만 화살은 정지한 것이 아니다. 느린 셔터로 찍었을 때보다 좀 더 선명해졌을 뿐 시간이 정지한 게 아니다. 셔터가 열리는 동시에 셔터가 닫히는 일은 불가능하기 때문이다. 실제로는 '한순간'에도 시간의 길이가 있는 것이다.
2-4. 경기장의 역설
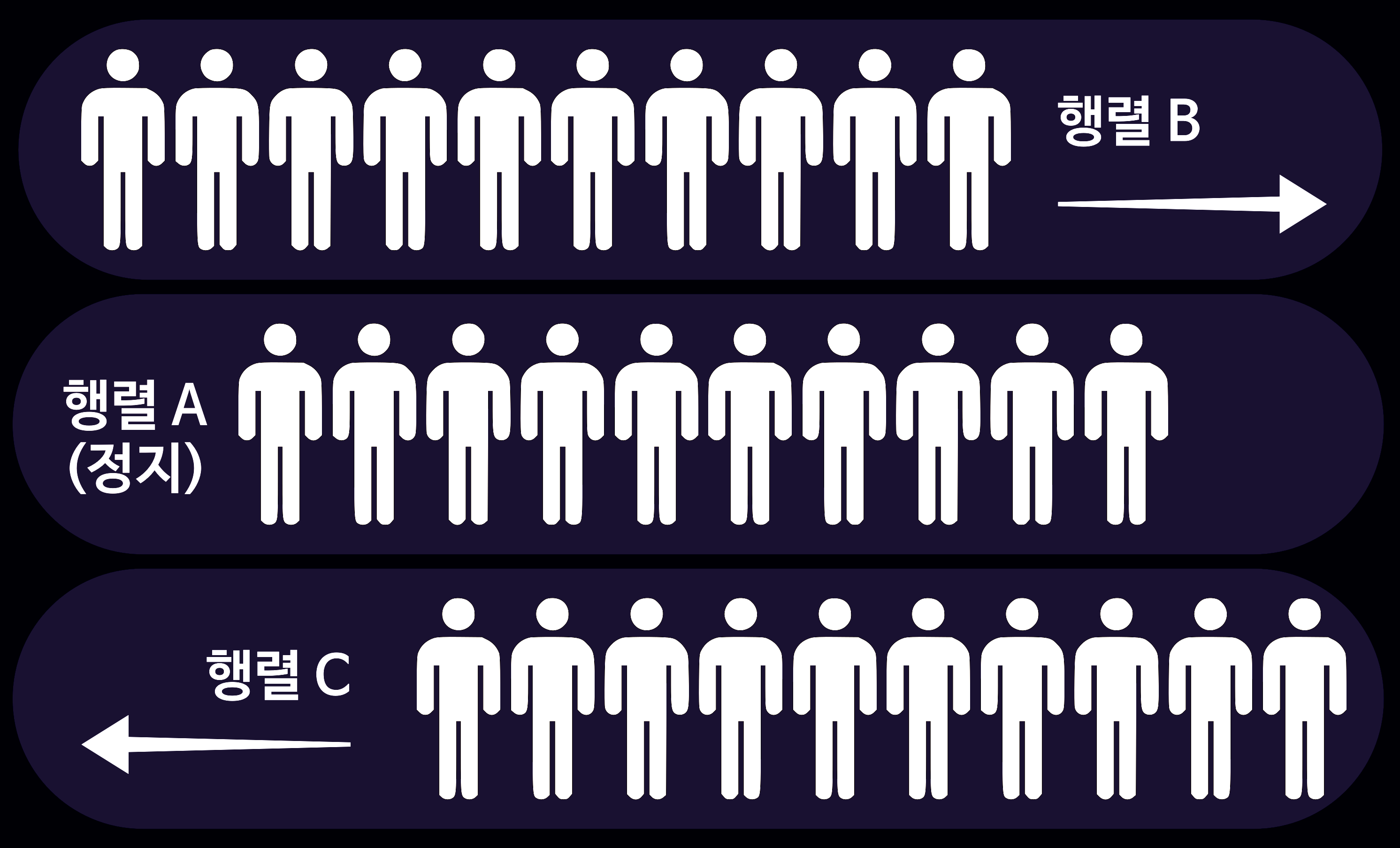
네 번째로 소개할 '제논의 역설'은 '경기장의 역설(Stadium Paradox)'이다. 사람들의 체격과 수가 동일하게 구성된 세 개의 행렬이 경기장에 줄 맞춰 있다고 가정하자. 하나의 행렬(A)은 멈춰있고 나머지 두 행렬(B, C)이 동일한 속도로 서로 반대 방향으로 움직일 때, B행렬에 있는 사람은 A행렬에 있는 사람 한명을 지나치는 시간 동안 C행렬에 있는 사람을 2명 지나치게 된다. 동일한 시간 동안 같은 속도로 움직이지만, 움직임의 양이 달라지는 것이다. 이 역설들은 운동이나 '무한(infinite)'이 실재한다고 가정했을 때 생기는 문제들을 보여준다.
2-5. 양자역학으로 보는 제논의 역설
오늘날의 '양자역학(Quantum Mechanics)'에서도 제논의 정신나간 주장을 단칼에 박살 내 버린다. 양자역학에서는 '무한히 작은 시간'과 '무한히 작은 거리'의 존재 자체를 부정해 버린다. 양자역학에서는 최소한의 길이 단위인 '플랑크 길이(Planck Length)'와 와 최소한의 시간인 '플랑크 시간(Planck Time)'이 존재한다. 따라서 아무리 시간과 길이를 잘게 분할해도 길이와 시간은 0이 되지 않는다.
제논은 그럴듯한 궤변으로 사람들을 현혹시킨다는 이유로, 사형을 당했다고 한다.
3. 갈릴레이의 역설
'전체'와 '부분' 중에서 어느 게 더 클까? 여러분들은 아마 '당연히 전체가 더 크다'라고 생각할 것이다. '부분'은 당연히 '전체'의 한 요소에 지나지 않기 때문에 이 논리에는 아무런 문제가 없어 보인다. 그런데 이 당연해 보이는 사실이 받아들여지지 않는 경우가 있다면 믿을 수 있겠는가?
짝수는 자연수의 '부분'이라고 할 수 있다. 예를 들어보자. 1~100의 자연수 중에는 짝수가 50개 포함되어 있다. 따라서 자연수는 100개이고 짝수는 50개이므로 당연히 '전체'가 '부분'보다 크다. 그런데 이번에는 자연수와 짝수의 관계를 생각해보자. 유한 집합이 아닌 무한 집합에서 말이다. 자연수는 무한 개고 짝수 또한 무한 개다. 따라서 자연수의 수와 짝수의 수는 같다.
이쯤에서 계산이 빠른 사람이라면 눈치챘겠지만, '전체가 부분보다 크다.'는 사실은 유한한 집합에서만 성립된다. 무한한 집합에서는 '전체가 부분보다 크다.'라는 사실이 성립되지 않는다. 이 사실을 최초로 제시한 사람이 바로 '갈릴레오 갈릴레이(Galileo Galilei, 1564~1642)'였는데, 그래서 이 역설을 '갈릴레이의 역설(Galileo's Paradox)'이라고 한다.
이후 독일의 수학자 '게오르크 칸토어(Georg Cantor, 1845~1918)'가 '무한 집합에 농도가 있다'는 새로운 개념을 제시하였다. 자연수와 부분집합인 짝수는 1:1로 대응시켜 모두 셀 수 있다. 하지만 선분 같은 경우에는 어떠한 조그만 구간을 잘라내도 길이가 0인 점은 그 안에 무한히 존재한다. 따라서 선분 안의 부분집합인 '점'을 모두 세는 것은 불가능하다. 이처럼 무한은 모두 셀수 있는 무한, 모두 셀 수 없는 무한이 존재한다. 그래서 '게오르크 칸토어'는 이를 설명하기 위해 '농도(Cardinality)'라는 개념을 도입하였다. '게오르크 칸토어'는 '자신과 같은 농도를 가진 진부분 집합이 존재하는 집합을 무한 집합'이라 정의하였다.

4. 톰슨의 램프
'톰슨의 램프(Thomson's Lamp)'라고 불리는 간단한 사고 실험 하나를 소개한다. '아킬레우스와 거북이의 역설(Achilles and the Tortoise Paradox)'과 비슷한 사고 실험이라서 어떤 사람은 이 사고 실험을 '제논의 역설(Zenon's Paradoxes)'의 아류작이라고 평가하기도 한다.
영국의 수학자 '제임스 톤슨(James Thomson, 1921~1984)'은 다음과 같은 실험을 고안했다. 여기에 조금 특이한 램프가 있다. 이 램프는 불이 켜진 1분 후에 불이 자동적으로 꺼지고 다시 30초 후에 불이 꺼진다. 그리고 15초 후에 불이 다시 꺼진다. 또다시 7.5초 후에 불이 켜지고.. 3.75초 후에 불이 꺼진다. 이런 식으로 점등 시간 또는 소등 시간은 정확히 절반의 시간이 지날 때마다 끝없이 되풀이된다. 이때 램프가 켜지거나 꺼진 시간을 다 합쳐보자. 결국 2분에 수렴한다. 그러면 정확히 2분이 지난 후에는 이 램프는 꺼져 있을까? 켜져 있을까?
2분이 지났을 때 램프가 켜져 있었다고 가정해 보자. 그러면 그 직전에 켜져 있던 순간이 있었을 것이다. 하지만 규칙에 의하면, 그 불은 켜져 있을 때의 대기 시간의 지나면 다시 꺼지기 때문에 2분이 되기 전에 꺼지게 된다. 그러면 반대로 2분이 지났을 때 램프가 꺼져있었다고 가정해 보자. 그러면 그 직전에 꺼져 있던 순간이 있었을 것이다. 하지만 규칙에 의하면 그 불은 꺼져 있을 때의 대기 시간의 지나면 다시 켜지기 때문에 2분이 되기 전에 켜지게 된다.
결국 2분에 램프가 켜져 있었다고 가정해도 꺼져있었다고 가정해도 모두 모순이 발생한다. 따라서 2분에 불이 켜져 있다고도 꺼져있다고도 말할 수 없다. 사실 '톰슨의 램프' 문제는 '가장 큰 자연수는 짝수인가? 홀수인가?'라는 질문을 그럴듯하게 바꿔논 것에 불과하다. 결론적으로 이런 램프는 세상에 존재할 수가 없다.

5. 2=1의 증명?
정삼각형을 이용해서 '2=1'을 증명하는 과정을 소개하겠다. 이 논리는 옳은 것일까?
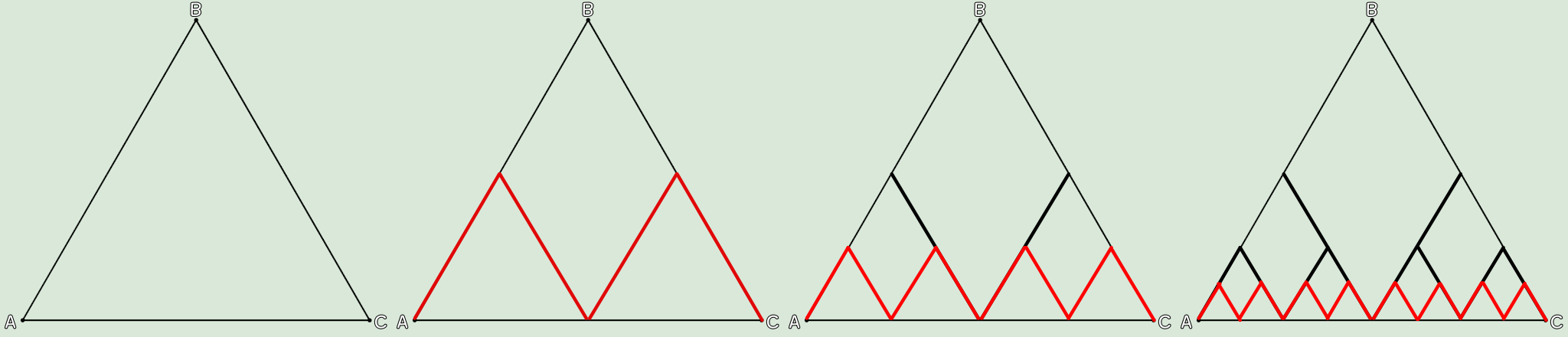
여기에 모든 변의 길이가 1인 정삼각형이 있다. 여기에 변 AB와 변 BC의 중점에서 변 AC의 중점을 향해 선을 그어보자. 이렇게 하면 변의 길이가 1/2인 삼각형이 두 개 생긴다. 한편 새로 생긴 정삼각형의 위쪽 변을 따라 A에서 C로 향하는 꺾은선들은 길이가 1/2인 선분 4개로 이루어져 있다. 꺾인 선들의 길이의 합은 2가 된다. 마찬가지로 길이가 1/4인 정삼각형을 만들면, 역시 위쪽 변을 따라 A에서 C로 향하는 꺾은 선들은 길이가 1/4인 선분 8개가 된다. 역시 꺾인 선들의 길이의 합은 2가 된다. 이 과정을 무한히 반복하면 꺾인선은 직선 AC와 같아질 것이다. 꺾은선의 길이의 합은 2, 직선 AC의 길이는 1이기 때문에 결국 2=1이 되는 것이다.
이 논리는 옳은 것일까? 결론부터 말하자면, 이 증명은 틀렸다. 이는 무한의 작업을 계속하면 꺾은 선이 AC와 같아진다는 논리에 오류가 있는 '패러독스(Paradox)'다. 삼각형을 무한히 작게 만들어나가다 보면 직선 AC와 비슷해지는 것처럼 보이지만 실제로는 일치하지 않는다. 일치할 수 없다.