-
원주율 π과학(Science)/수학 (Math) 2023. 4. 2. 17:16
'원주율(pi ratio)'이란 '원 둘레의 길이'를 '지름'으로 나눈 값으로 'π(파이)'라는 그리스 문자로 나타낸다. 초등학교에서는 약 3.14라고 배우지만, 실제로는 3.14 뒤에 규칙성 없는 숫자가 무한히 늘어선다. π의 정확한 값을 구하는 데 처음으로 도전한 사람은 고대 그리스의 '아르키메데스'였다. 그 정열은 후대의 수학자에게 계승되었으며, 원주율 π값의 기록은 2000년 이상 지난 지금까지도 계속 갱신되고 있다. 원주율 π에 숨겨진 신비한 성질에 대해 알아보자.
0. 목차
- '원주율 π'란 무엇인가?
- 고대의 원주율 계산 방법
- 직접 실험해서 π값 구하기
- π와 무한
- 무한급수로 π를 나타내는 방법
- 컴퓨터에 의한 π의 계산
- π와 소수는 연결되어 있었다.

1. '원주율 π'란 무엇인가?
1-1. π는 무리수이다.
'실수(Real number)'에는 '유리수(Rational Number)'와 '무리수(Irrational Number)'가 있다.
- 유리수(Rational Number): '유리수'란 정수를 '분자와 분모로 가지는 분수(분모 0은 제외)'로 나타낼 수 있는 수이다. '정수' 자신은 분모를 1로 하는 분수라고 생각할 수 있으므로 유리수이다. 유리수에는 소수점 아래에 숫자가 무한하게 계속되는 수가 있다. 예를 들어 1/3=0.3333......이나 1/7=0.142857...... 등이다. 그러나 이들은 π와 달리 특정한 수가 순환하는 '순환 소수'이다.
- 무리수(Irrational Number): '무리수'란 유리수처럼 정수의 분수로 나타낼 수 없는 수를 말하며, 소수점 아래에 순환하지 않는 수가 계속된다. 따라서 π는 무리수이다. π 외에도 '√ 2(제곱하면 2가 되는 수)' 등도 대표적인 무리수이다.
1-2. 원주율의 난수적 성질
'원주율 π'의 정확한 값을 구하려는 시도는 고대 그리스의 '아르키메데스(Archimedes, 기원전 287?~212?)'부터 시작되어 그 후로도 많은 수학자가 도전했다. 2021년 8월에는 62조 8000억 자리라는 신기록이 수립되었지만, 앞으로도 기록은 계속 늘어날 것이다. '원주율 π'는 어디까지나 정확하게 구하더라도 그 다음 이어지는 수는 전혀 알 수 없다. 이 점이 많은 과학자가 원주율에 매력을 느끼는 이유일지도 모른다.
뭐라도 좋으니 10자리 숫자의 열을 떠올려 보자. 그러면 여러분이 떠올린 그 숫자의 열은 원주율 안에 반드시 들어있다. 원주율 π는 불규칙적인 수가 무한히 계속되므로, 특징적인 수열이 우연히 출현하는 경우가 있다. 예를 들어 4444444444이나 6666666666 이외에 1234567890이나 0987654321처럼 양 끝이 0이면서 자연수가 크기순으로 차례로 배열되는 수열 등도 여러 곳에 있다. 만약 각 숫자가 출현하는 빈도가 완전히 무작위적이라면 π는 어디까지나 무한히 계속될 수이므로 그 안에는 반드시 떠올린 숫자가 등장할 것이다. 예컨대 휴대전화 번호도 반드시 어디엔가 들어있다.
그러면 원주율의 소수점 아래에 각 숫자가 출현하는 빈도는 정말 완전히 무작위일까? 인류는 19세기까지 손으로 계산해 527자리까지 원주율을 구했고, 20세기 중반에 들어와 컴퓨터가 등장하면서 극적으로 자릿수가 늘어났다. 2021년에는 62조 8000억 자리까지 계산되었다. 자릿수와 함께 π 안에 0~9의 숫자가 얼마나 출현하는지도 조사되었다.
아래의 표는 π의 소수점 아래에 5조 자리 안에 0~9의 수가 출현하는 횟수이다. 자세히 보면 약간 차이는 있지만, 모든 수가 자릿수의 10분의 1인 5000억 회 정도 출현하고 있음을 알 수 있다. 지금까지 계산 결과만으로 보면, 각각의 숫자가 거의 같은 빈도로 나타나고, 각수의 출현 방식에 규칙성은 확인되지 않는다. 나아가 모든 숫자의 출현 빈도가 자릿수가 늘어남에 따라 거의 균등해지는 것을 알 수 있다. 그래서 π의 숫자 배열은 모든 숫자가 같은 확률로 무작위적으로 출현하는 '난수(Random Number)'라고 생각되고 있다. 그러나 π의 숫자가 정말 '난수'인지는 증명되지 않았다.
숫자 출현 빈도 0 4999억 9897만 6328회 1 4999억 9996만 6055회 2 5000억 0070만 5108회 3 5000억 0015만 1332회 4 5000억 0026만 8680회 5 4999억 9949만 4448회 6 4999억 9893만 6471회 7 5000억 0000만 4756회 8 5000억 0121만 8003회 9 5000억 0027만 8819회 2. 고대의 원주율 계산 방법
π의 값은 원을 같은 크기의 넓이를 가진 정사각형으로 변환함으로써 근삿값을 구할 수 있다. 어떤 크기의 원을 같은 크기의 넓이를 가진 정사각형으로 변환하는 문제는 오래전부터 세계 각지에서 다루어졌으며, 그 역사도 길다. '바빌로니아 시대'와 '고대 이집트 시대'로 잠시 돌아가 보자.
반응형2-1. 바빌로니아 시대
- 바빌로니아 시대의 원주율: 3.125
인류는 적어도 기원전 5000년 무렵부터 수레바퀴 같은 원형의 물체를 사용해 무거운 것을 운반하는 식으로 '원(Circle)'을 도움이 되는 형태를 인식하고 이용했다. 특히 원에 관해 높은 수학적 지식을 가졌던 사람들이 현재 이라크 남부에 해당하는 지역에 기원전 2500년 무렵부터 살고 있던 '바빌로니아인'이다. 그들은 원을 연구에 원둘레 길이가 원의 지름에 비례하는 것, 즉 원주율의 존재를 알아차렸다.
'바빌로니아인'이 점토판에 쐐기 모양의 문자를 새겨 햇볕에 말려 굳힌 것이 보존되어 대량으로 전해지고 있다. 그 점토판으로부터 바빌로니아인이 기원전 2000년 무렵까지 '원둘레 길이를 구하는 계산식'을 사용했음이 알려졌다. 그런 식의 하나로부터 원주율을 구하면, 3+1/8=3.125라는 값이 된다. 당시에 그런 계산은 토지 등의 크기를 재는 데 사용되었으며, 점토판을 통해 바빌로니아인들이 토지 크기에 따라 세금 등을 지불했음을 엿볼 수 있다.
바빌로니아인이 어떻게 3+1/8이라는 값에 이르게 되었는지는 정확하게 알려져 있지 않다. 그러나 현대의 우리가 그들과 같은 결론에 이르는 간단한 실험을 해보면 된다. 예를 들어 끈의 양 끝에 나무 막대를 동여매고 지면에 원을 그려보자. 그리고 끈을 그대로 자 대신으로 해서 지면에 그린 원의 둘레를 잰다. 그러면 원 둘레는 끈의 길이 6개만큼 보다 약간 길다. 6개를 재고 남은 나머지는 끈을 4등분 한 길이와 대략 같음을 알 수 있다. 이 점에서 원 둘레는 원의 반지름의 약 6과 1/4배, 즉 지름으로 고치면 3과 1/8이 되어 바빌로니아인의 계산식으로 구한 원주율 π의 값과 일치한다.
2-2. 고대 이집트 시대
- 고대 이집트인의 원주율: 3.160...
기원전 3000년 무렵부터 시작된 고대 이집트 왕조 시대에 원의 넓이를 구한 방법도 '파피루스(고대 이집트의 종이)'에 상형 문자 '히에로글리프'로 기록되어 남아있다. 거기에는 '지름이 9인 원의 넓이는 1변이 8인 정사각형의 넓이와 같다'는 기술이 있으며, 그 기술을 바탕으로 역산하면 원주율 π는 4×(8/9)2=3.16049......가 된다.

고대 이집트의 '파피루스'에 남겨진 계산 2-3. 원적문제
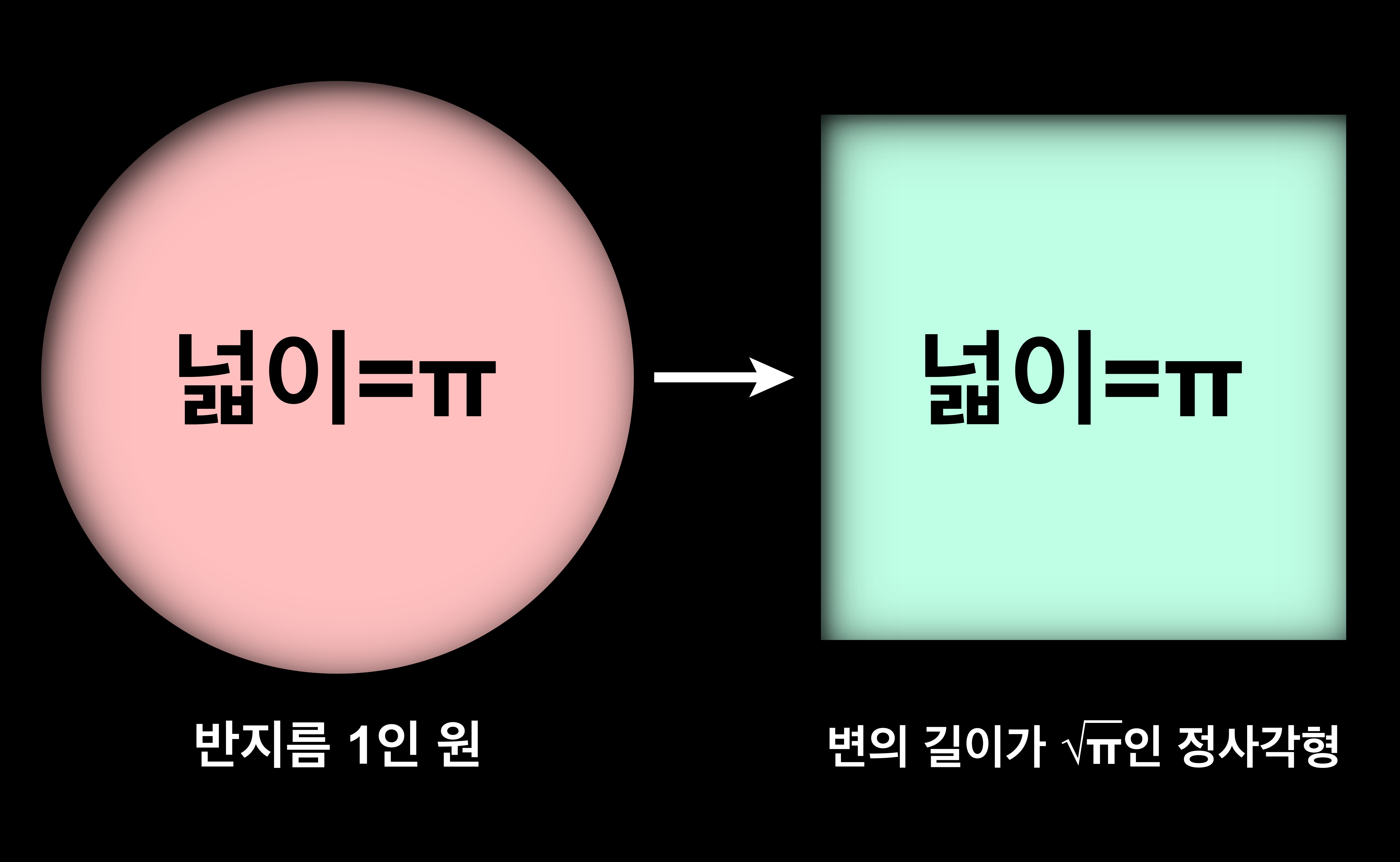
'원을 같은 넓이의 정사각형화하는 것'을 '원의 정사각형화'라고 하며, 이것은 고대 이집트 시대부터 다루어져 왔다. 고대 그리스에서는 이 문제에 난이도를 더해 '주어진 원과 같은 넓이를 가진 정사각형을 자와 컴퍼스를 이용한 유한 횟수의 조작으로 작도할 수 있을까?'라는 문제가 고안되었다. 이것이 바로 그 유명한 '원적문제(Quadrature of a Circle)'이다. '원적문제'는 오랫동안 수학자들을 괴롭혔다. 그리고 19세기 후반이 되어서야 마침내 원적문제는 풀 수 없음이 증명되었다. 그런데 근사의 해를 작도하는 방법이나 자와 컴퍼스 이외의 도구를 사용한 해법은 많이 알려져 있다.
원의 넓이는 반지름×반지름×π이므로, 반지름을 1이라 하면 넓이는 π가 된다. 넓이가 π인 정사각형 1변의 길이는 √π가 된다. 즉 '원적문제'는 '길이 1이 주어졌을 때 길이 √π인 선분을 작도할 수 있을까?'라는 문제로 바꾸어 말할 수 있다. 실은 길이 1이 주어지면 컴퍼스와 자를 유한 횟수로 사용함으로써 유리수 길이의 선분은 모두 작도할 수 있다. 또 √2, √3, √5 같은 일부 무리수 길이의 선분도 작도할 수 있다. 그러나 무리수 가운데는 아무리 해도 작도할 수 없는 수가 있음이 알려져 있는데, 그것이 바로 '초월수(Transcendental Number)'이다. '초월수'란 무리수 가운데서도 'n차 대수 방정식(n은 자연수이며 방정식의 계수는 모두 유리수의 상수)'의 해가 되지 않는 수이다. √2는 x2=2라는 방정식의 해가 되므로 초월수는 아니다. √2처럼 방정식의 해가 되는 무리수를 대수적 무리수라고 한다. 만약 π가 초월수면 √π도 초월수가 된다. 즉 π가 초월수임이 증명되면 원적문제는 풀 수 없음을 자동적으로 증명한 셈이 되는 것이다.
그리고 1992년에 수학자 '페르디난트 폰린데만(Ferdinand von Lindemann, 1852~1939)'이 π가 초월수임을 증명함으로써, 마침내 원적문제를 풀 수 없음이 알려졌다. '페르디난트 폰린데만'은 '오일러의 공식'을 사용해 π가 초월수임을 증명했다. 초월수는 무수히 있음이 알려져 있지만, 실제로 알려진 초월수는 'π'나 '자연로그의 밑 e(네이피어수)' 등 극소수밖에 없다. π+e나 π×e조차 초월수인지 아닌지 알려져 있지 않다. 원적문제라는 난제는 풀 수 없다는 사실이 알려졌지만, 초월수에는 아직 많은 남제가 많이 남아 있다.
원적문제(Quadrature of a Circle) 2-4. '정다각형'을 이용해 π의 값 구하기
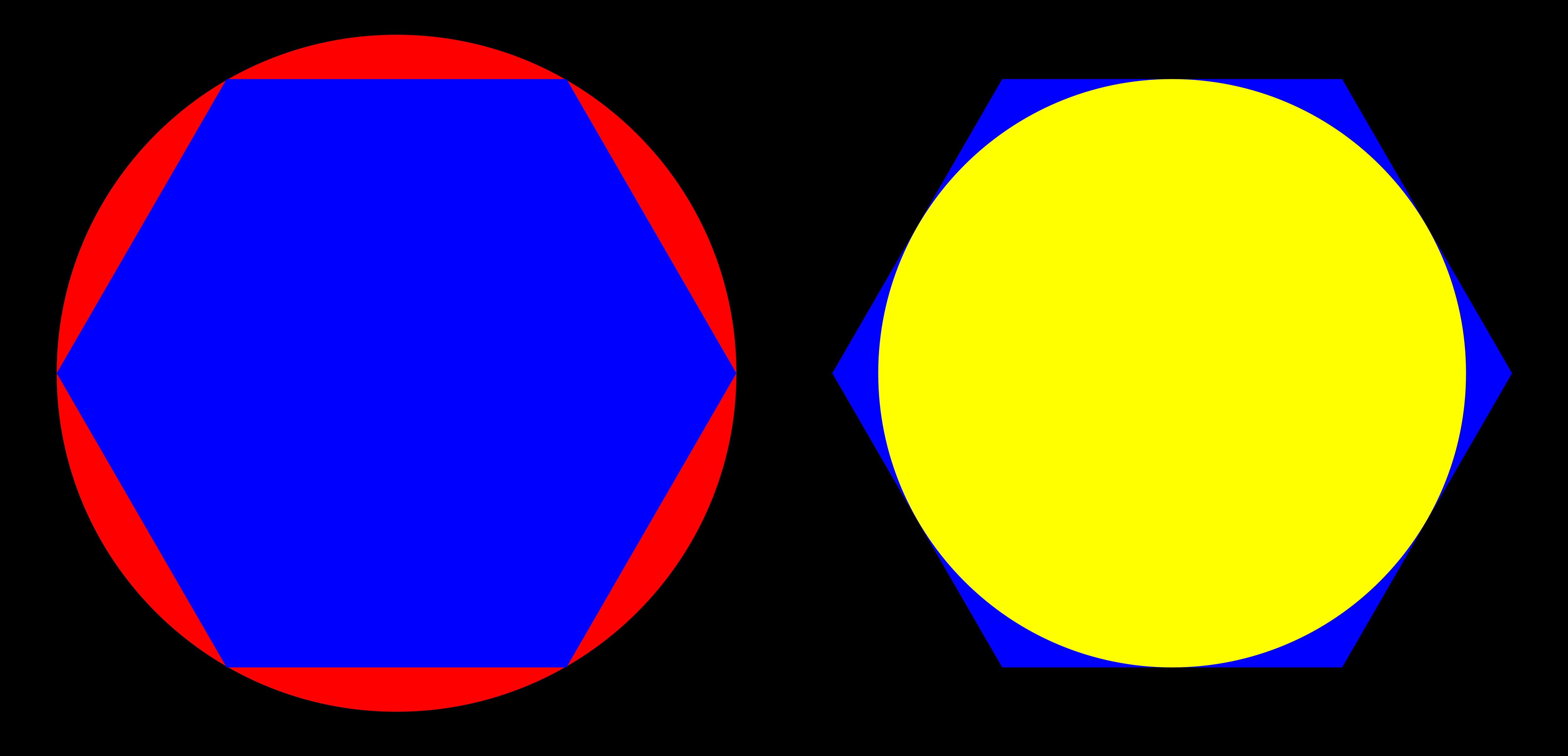
기원전 3세기에 들어와 원주율의 참값에 끝없이 가까워질 수 있는 획기적인 방법을 생각해 낸 사람이 나타났다. 고대 그리스의 수학자이자 물리학자인 '아르키메데스'이다. '아르키메데스'가 생각해낸 방법은 다음과 같다. 먼저 원의 안쪽에 접히는 정6각형과, 원의 바깥쪽에 접히는 정6각형을 생각한다. 아르키메데스는 정6각형 바깥둘레 길이와 원둘레 길이를 비교해 원주율이 취할 수 있는 범위를 좁혀 가는 방법을 생각한 것이다. 정6각형을 사용하면 원주율 π의 범위가 3<π<3.4641......이 된다.
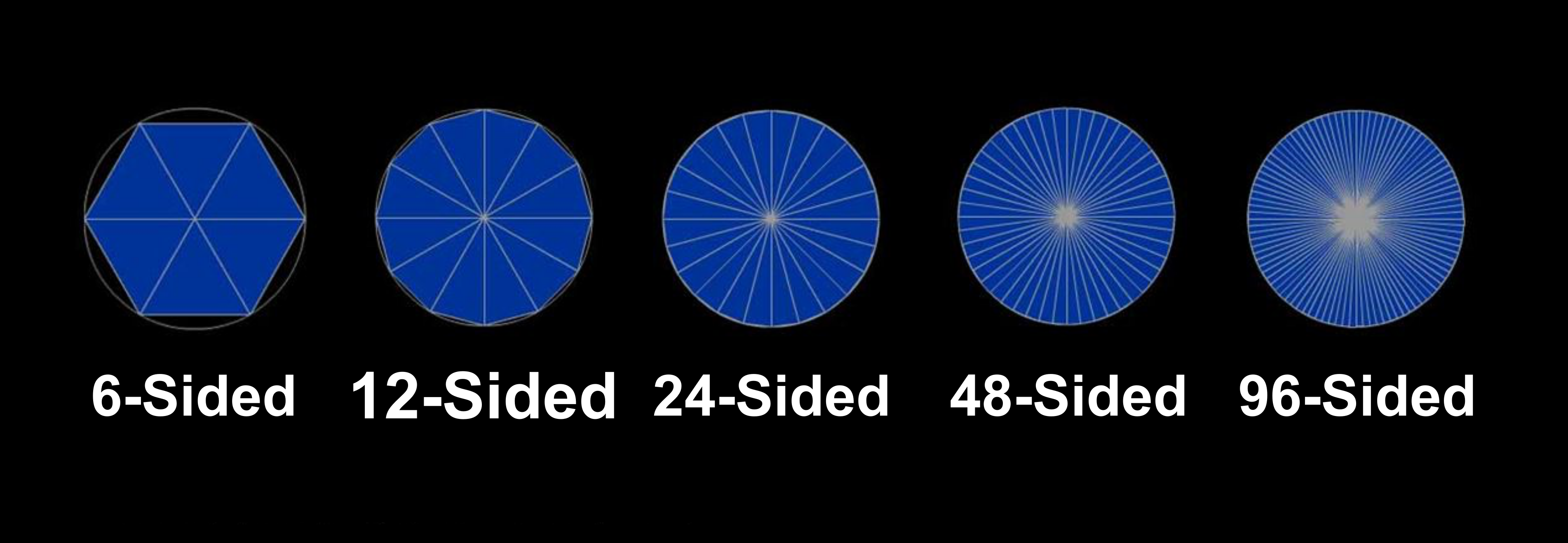
아르키메데스는 이 방법을 확장해 정12각형, 정24각형, 정48각형, 정96각형 등과 같은 식으로 원에 내접·외접하는 정다각형 변의 수를 차츰 늘렸다. 정다각형 변의 수를 끝없이 늘리면 정다각형과 원 사이의 틈새는 차츰 작아지고 끝없이 원 모양에 가까워진다. 최종적으로 아르키메데스는 정 96각형을 사용함으로써 3.1408......<π<3.1428......이라는 부등식을 얻는 데 성공했다. 이 아르키메데스의 식에 의해 π의 값은 소수점 아래 2자리, 즉 3.14까지 확정된 셈이다.
이 방법은 원리적으로는 π의 실제값에 무한히 가까워질 수 있다는 점에서 획기적이었다. 아르키메데스 이후 수학자들은 지속적으로 정다각형 변의 수를 늘렸다. 16세기에는 독일 태생의 네덜란드 수학자 '뤼돌프 판 쾰런(Ludolph van Ceulen, 1540~1610)' 무려 정 262(약 461경 1686조)'각형을 사용해 소수점 아래 35자리까지 정확한 π의 값을 구했다. 그렇지만 이 방법은 정다각형 변의 수를 늘릴 때마다 서로 다른 계산식을 사용해 계산을 수정해야 하기 때문에 계산 양이 크게 증가한다. '뤼돌프 판 쾰런(Ludolph van Ceulen)'이 했던 손 계산이 얼마나 힘든 작업이었는지는 쉽게 상상할 수 있다. 또 이 방법은 계산 양에 비해 구해지는 값의 자릿수가 많지 않다. 그러나 아르키메데스 이후 유럽에서는 16세기가 될 때까지 오랫동안 π의 새로운 계산 방법이 발견되지 않았다.
3. 직접 실험해서 π값 구하기
3-1. 몬테카를로법
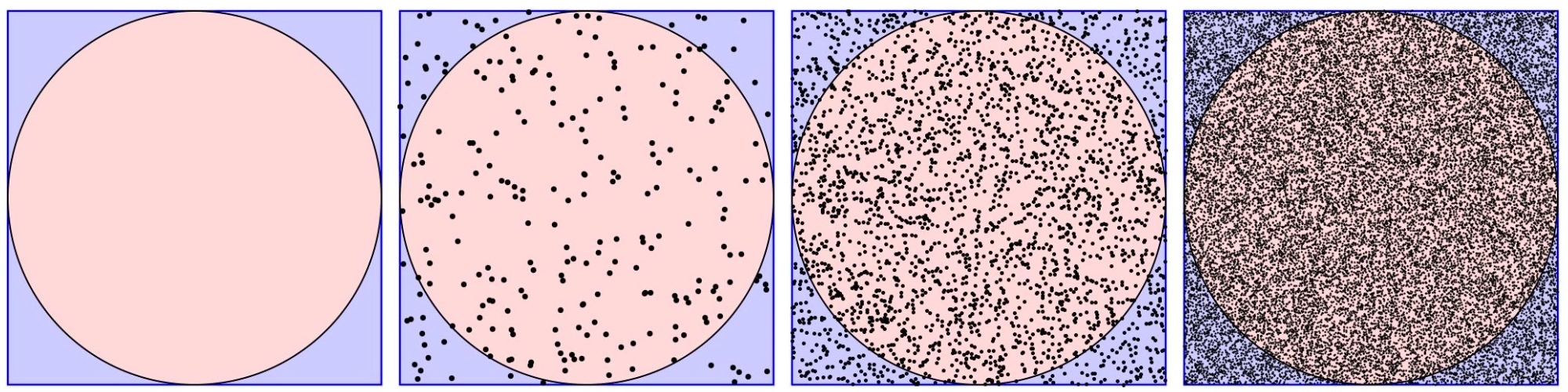
이번에는 직접 실험을 해서 π의 근삿값을 구하는 방법을 알아보자. 1변의 길이가 2인 정사각형과 그 정사각형 내에 접하는 원을 생각해 보자. 정사각형의 넓이는 2×2=4, 원의 넓이는 반지름×반지름×π이므로 1×1×π=π이다. 따라서 정사각형 넓이 : 원의 넓이 = 4 : π가 된다. 여기서 정사각형을 향해 위에서 무작위로 점을 찍는 실험을 한다. 이때 정사각형 전체에는 떨어지는 쌀알의 수와 정사각형에 내접하는 원 안에 찍히는 점의 수를 비교하면 넓이의 비와 마찬가지로 4 : π가 될 것이다. 이것을 이용해 정사각형 전체에 찍힌 점의 수와 내접하는 원 안에 찍힌 점의 수를 헤아려 그 비를 구함으로써 π의 근삿값을 구할 수 있다. 점의 수를 늘리면 늘릴수록 그 값은 3.141592......에 가까워질 것이다.
하지만 실제로 점을 찍는 것은 힘들고, 찍을 수 있는 점의 개수에도 한계가 있다. 또 정말로 점이 무작위로 찍힌다는 보증도 없다. 그래서 현재는 컴퓨터 시뮬레이션을 사용해서 실제 점을 찍는 것과 같은 실험을 할 수 있다. 먼저 컴퓨터가 만들어낸 난수에 의해 정사각형 안의 무작위적 위치에 점을 찍는다. 그중에서 정사각형에 내접하는 원 안에 존재하는 접의 수의 비율을 계산한다. 그렇게 함으로써 수작업으로 점을 찍지 않고 원주율 π의 근삿값을 구할 수 있다.
이처럼 컴퓨터가 만드는 난수에 의해 어떤 사건이 초래할 값을 구하는 방법을 '몬테카를로법(Monte Carlo Method)'이라고 한다. π의 계산은 어디까지나 몬테카를로법의 응용 사례 가운데 하나이며, 실제로는 공학의 여러 분야에서 사용되고 있다. 참고로 '몬테카를로'는 카지노로 유명한 '모나코(Monaco)' 공국의 지역 이름이다. 컴퓨터 '에니악(ENIAC)'의 개량에 관여한 것으로 유명한 '존 폰 노이만(1903~1957)'이 명명했다. '에니악'은 제2차 세계 대전 중 미국 육군이 대포의 탄도 계산을 하기 위해 개발된 컴퓨터로, 세계 최초로 π를 계산한 컴퓨터이기도 하다.
몬테카를로법(Monte Carlo method) 3-2. 뷔퐁의 바늘
실험으로 π의 값을 구하는 방법은 더 있다. 그중 하나로 여기에서는 '뷔퐁의 바늘(프랑스어: L'aiguille de Buffon)'을 소개한다. 이것은 평행하게 선이 그어진 바닥 위에 바늘을 떨어뜨리는 실험으로 원주율 π의 근삿값을 구하는 방법이다. 프랑스의 수학자 '조르주루이 르클레르 드 뷔퐁(Georges Louis Leclerc de Buffon, 1707~1788)'은 1777년에 발표한 논문 '정신적 산술론'에서 π에 관한 다음과 같은 문제를 제시했다. 먼저 종이를 1장 준비한다. 그 종이 전체에 자로 같은 간격으로 평행인 직선을 긋는다. 직선끼리의 간격은 d라고 한다. 그다음에 길이 L인 바늘을 준비한다. (단, 바늘의 길이는 직선끼리의 간격보다 작음) 이 바늘을 직선을 그은 종이 위에 무작위로 여러 번 떨어뜨린다. 이때 바늘이 자로 그은 선과 교차할 확률 P는 얼마나 될까?
'뷔퐁'은 논문에서 '확률 P는 2L/πd'라고 했다. 실은 이 문제는 '뷔퐁'의 발표 뒤 35년 동안이나 잊혀져 있었다. 그것을 발견해 빛을 보게 한 것이 프랑스의 수학자 '피에르 시몽 라플라스(Pierre Simon Laplace1749~1827)'였다. 뷔퐁이 구한 식을 변형하면 π=2L/Dp이 된다. 바늘의 길이와 평행선의 간격을 같게 하면 L/d=1이 되어 π=2/P가 된다. '피에르 시몽 라플라스'의 아이디어는 '그렇다면 실제로 바늘을 떨어뜨려 확률 P의 값을 얻으면 π가 구해지지 않을까?'하는 것이었다.
'P=바늘이 직선에 교차한 횟수 ÷ 바늘을 떨어뜨린 횟수'로 나타낼 수 있다. π의 근삿값을 구하려면 바늘을 떨어뜨린 횟수와, 그들 가운데 직선에 교차한 바늘 개수만 기록하면 된다는 것이다. 바늘을 떨어뜨리는 횟수를 늘리면 늘릴수록 π를 정확하게 구할 수 있다. 실제로 1901년에 이탈리아의 수학자 '마리오 라차리니(Mario Lazzarini)'가 바늘을 3408회 떨어뜨려 π=3.1415929라는 근삿값을 얻었다. 그러나 이것은 기적적으로 참값에 가까운 값이 얻어진 예로서, 통상적으로는 1만 회 떨어뜨려 소수점 2자리 즉, (3.14......)까지 구하는 것이 고작인 것 같다.
바늘을 계속 떨어뜨리는 것은 힘든 작업이다. 그래서 컴퓨터로 시뮬레이션하여 무작위로 바늘을 배치함으로써 π를 구하는 아이디어가 나왔다. 실은 '뷔퐁의 바늘'은 이미 소개한 몬테카를로법이 만들어진 계기가 문제이기도 하며, 그 힌트를 준 사람이 '피에르 시몽 라플라스(Pierre Simon Laplace)'였다.

뷔퐁의 바늘(프랑스어: L'aiguille de Buffon) 4. π와 무한
4-1. 비에트의 공식
16세기 전반까지는 '아르키메데스'의 방법이 유럽에서 π를 구하는 유일한 방법이었다. 그러나 16세기 중반이 되자 새로운 방법이 고안되었다. 그것이 무한히 계속되는 식을 사용한 방법이었다. 가장 오래된 예가 √ 안에 √ 가 무한하게 들어간 '무한 다중 근호'를 사용해 π를 나타내는 식이다.
π를 무한 다중 근호로 나타낸 '비에트의 공식(Viète's formula)'은 프랑스의 수학자 '프랑수아 비에트(1540~1630)'가 유도한 것이다. '비에트의 공식'은 π를 최초로 하나의 식 형태로 나타냈다는 점에서 획기적이었다. '아르키메데스'의 방법은 다각형의 변의 수를 늘릴 때마다 서로 다른 식을 계산해야 했지만, 비에트 공식은 하나의 식을 계산하는 것만으로 π의 근삿값의 정확도를 무한하게 높일 수 있었다. 단, 비에트의 공식 자체는 근호의 계산이 어려우며, 게다가 계산해도 좀처럼 참된 값에 가까워지지 않기 때문에 정확한 π의 값을 계산한다는 목적에는 어울리지 않았다. 그 후 π의 값을 구하는 여러 가지 공식이 고안됨으로써 더 정확한 π의 값을 구할 수 있게 되었다.
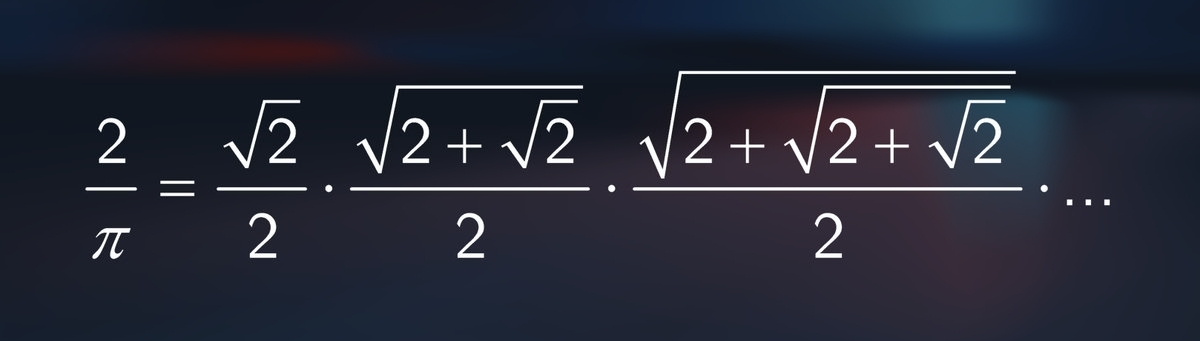
비에트의 공식 4-2. 브롱커의 공식(Bronker's Formula)
'무한 다중 근호'에 덧붙여 '연분수'를 사용해 π를 나타내는 방법도 등장했다. '연분수(Continued Fraction)'란 러시아 전통 인형인 '마트료시카(Matryoshka)'처럼, 분수의 분모 속에 다시 분수가 들어 있는 분수를 말한다. 예를 들어 √2는 무리수이므로 '정수의 분수(유리수)'로 나타낼 수 없지만, 연분수를 사용하면 놀랍게도 나타낼 수 있다.
17세기 후반 아일랜드 태생의 수학자 '윌리엄 브롱커(William Brouncker, 1620?~1684)'가 원주율 π의 연분수 표현을 고안했다. 그것이 '브롱커의 공식'이다. 이처럼 π는 자연수의 2제곱과 짝수가 차례로 나타나는 규칙 바른 연분수로 나타낼 수 있다. '윌리엄 브롱커'는 영국의 수학자 '존 월리스(1616~1703)'가 고안한 '윌리스의 공식'에서 '브롱커의 공식(Bronker's Formula)'을 유도했다고 한다.
반응형5.무한급수로 π를 나타내는 방법
17세기에는 유리수를 무한히 더하는 식에 의해 π를 나타내는 방법이 발견되었다. 그 대표적인 예가 '마드하마-그레고리-라이프니츠 급수'와 '마친의 공식'이다. 이처럼 무한히 더하는 형태로 나타낸 식을 '무한급수(Infinite Series)'라 한다. '무한급수'에는 '발사하는 무한급수'와 '수렴하는 무한급수'가 있다.
- 발산하는 무한급수: 먼저 간단한 무한급수를 생각해 보자. 예를 들어 1+2+3+4+5+.....처럼 자연수를 무한히 더하면 그 합이 무한대가 되는 것은 쉽게 상상할 수 있지 않을까? 이것을 수학에서는 '발산한다'고 한다. 그러면 1+1/2+1/3+1/4+1/5+......는 어떨까? 이 합도 발산하는 것이 알려져 있다.
- 수렴하는 무한급수: 이번에는 1+1/2+1/4+1/8+1/16+......처럼 분모가 2배씩 늘어나는 무한급수를 생각해 보자. 이것의 합은 '2'에 가까워지는 것이 알려져 있다. 이것을 '2에 수렴한다'고 표현한다.
5-1. 마드하바-그레고리-라이프니츠 급수
무한급수를 사용해 π를 나타내는 방법으로 처음 등장한 것이 '마드하바-그레고리-라이프니츠 급수(Madhava-Gregory-Leibniz Series)'였다. 무한히 이어지는 '홀수분의 1'에 대해 덧셈과 뺄셈을 번갈아 하면 놀랍게도 π/4에 수렴하는 것이다. 이 무한급수는 그 이름대로 인도의 '마드하바(1340~1424)', 스코틀랜드의 '제임스 그레고리(1638~1675)', 독일의 '고트프리프 라이프니츠(1646~1716)', 이 3명의 수학자가 각각 독립적으로 발견했다. '그레고니'와 '라이프니츠'에 의해 유명해졌기 때문에 '그레고리-라이프니츠 급수'라고도 했지만, 나중에 그들보다 300년 전에 '마드하바'가 이미 발견했음이 알려졌다.
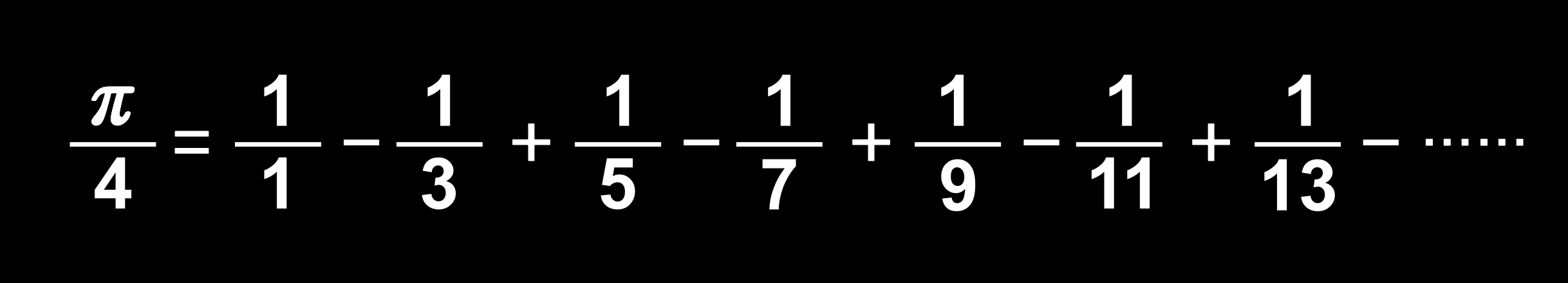
마드하바-그레고리-라이프니츠 급수(Madhava-Gregory-Leibniz Series) 5-2. 마친의 공식
확실히 이 '마드하바-그레고리-라이프니츠 급수'를 사용해 계산하면 π의 값이 어느 정도 정확하게 구해진다. 그러나 이 식은 매우 수렴이 느려 80만 항목까지 계산해야 고작 'π의 소수점 6자리(3.141592)'까지 밖에 실제 값과 일치하지 않는다. 그래서 새로운 무한급수가 연구되었다.
그 가운데서도 π의 계산에 큰 발전을 가져온 것이 영국의 천문학자이자 수학자인 '존 마친(John Machin, 1680?~1751)'이 발견한 '마친의 공식'이다. 이 식은 '마드하바-그레고리-라이프니츠 급수'에 비해 수렴이 빠린 것이 특징이다. 실제로 1873년에 영국의 '윌리엄 섕크스(William Sahnks, 1812~1882)'가 이 식을 사용해 π의 값을 소수점 아래 527자리까지 계산하는 데 성공했다.
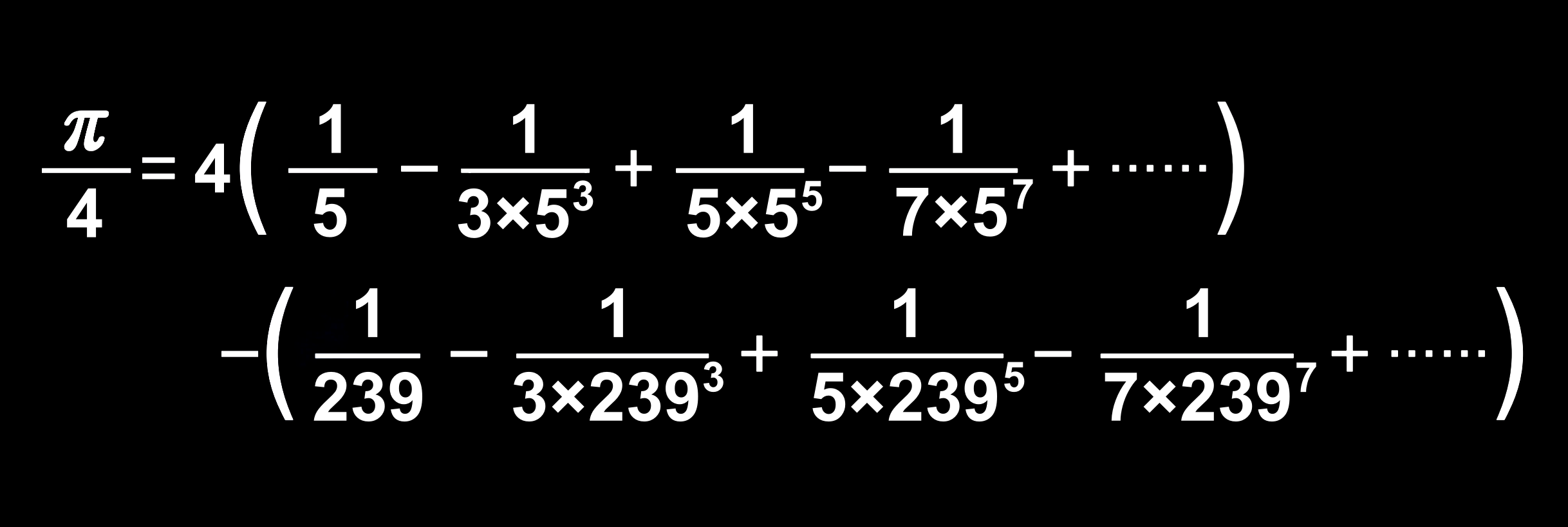
마친의 공식 5-3. 라마누잔의 원주율 공식
여러 가지 원주율 공식이 고안되어 있지만 그 가운데서도 눈에 띠는 것이 인도의 수학자 '스리니바사 라마누잔(Srinivasa Ramanujan, 1887~1920)'이 발견한 원주율 공식이다. 라마누잔의 공식은 복잡한 형태를 하고 있지만, 아주 빨리 정확한 π의 값에 수렴한다. 이 공식은 그의 노트에 적힌 많은 공식과 정리 가운데 하나이지만, 라마누잔은 그들의 증명을 일체 남기지 않았기 때문에 그의 사후에 여러 수학자들이 증명을 시도했다.
1985년에는 라마누잔의 원주율 공식을 사용해 미국의 수학자 '윌리엄 고스퍼(Ralph WIlliam Gosper)'가 π의 값을 1752만 6200자리까지 계산했다. 당시에 라마누잔의 식에 대한 수학적인 증명은 이루어지지 않았지만, '윌리엄 고스퍼'의 계산 결과는 놀랍게도 그때까지 얻어진 π의 값과 일치했다. 그리고 2년 뒤인 1987년에 라마누잔의 원주율 공식이 옳다는 것이 수학적으로 증명되었다.
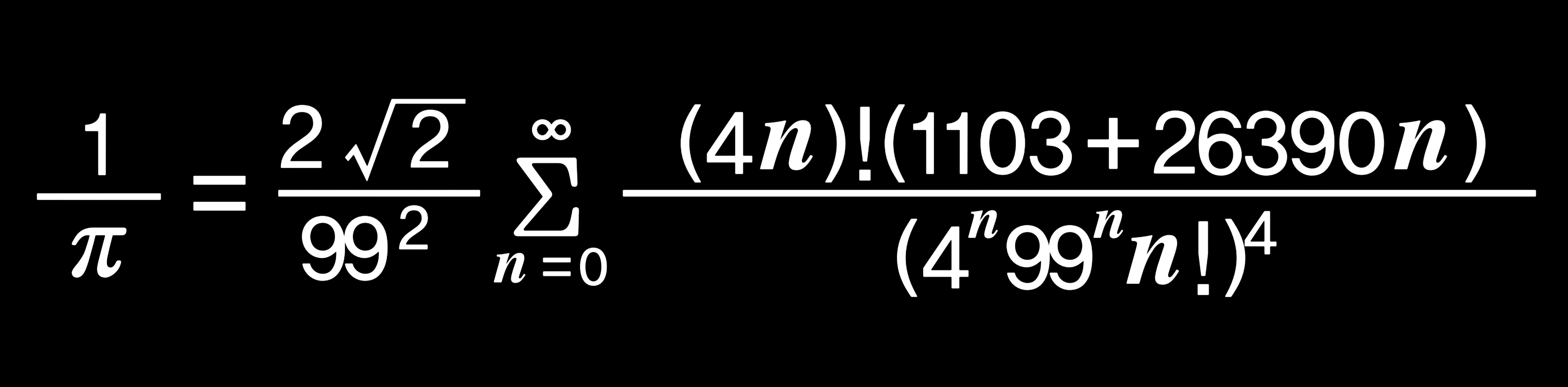
라마누잔의 원주율 공식 
스리니바사 아이양가르 라마누잔(1887~1920) 6. 컴퓨터에 의한 π의 계산
컴퓨터가 급속히 발전한 1940년대 이후, π의 계산은 컴퓨터를 사용해 이루어졌다. 세계 최초로 π를 계산한 컴퓨터는 '에니악(ENIAC)'인데, 1949년 9월의 일이었다. 에니악은 2037자리까지의 π의 값을 70시간 걸려 계산했다. '윌리엄 섕크스(William Sahnks, 1812~1882)'가 생애를 바쳐 계산한 π의 근삿값의 자릿수를 단지 70시간 만에 3배 이상이나 넘어선 것이다. 에니악에서의 π 계산에는 '마친의 공식'이 사용되었다. 그 후 컴퓨터의 처리 속도가 기하급수적인 발전을 계속하면서, π의 근삿값 자릿수도 극적으로 늘어났다.
컴퓨터 처리 속도가 상승한 것과 함께 계산식에 관해서도 '스퇴르메르의 공식' 등 새로운 식이 발견되거나 효율적인 컴퓨터의 계산 알고리즘이 차례로 개발되었다. 이러한 공식과 알고리즘의 개발에 따라 계산에 걸리는 시간도 점점 짧아졌다. 애니악의 등장 이후 불과 수년 뒤인 1950년대에는 이미 1만 자리를 돌파했고, 1961년에는 스퇴르메르 공식을 사용해 자릿수가 10만 자리를 돌파했으며, 1973년에는 미국의 컴퓨터 'CDC7600'이 100만 1250자리를 기록했다. 1980년대에는 도쿄 대학교 정보 기반 센터의 '가나다 야스마사' 교수의 연구팀이 차례로 기록을 경신했다. '가나다 야스마사' 교수의 연구팀은 1989년 11월에 10억 7374자리를 달성했다. 그 후 슈퍼컴퓨터의 등장으로 기록은 계속 갱신되었다. 2021년 8월에 발표된 π의 세계 기록은 무려 62조 8000억 자리였다. 이것은 스위스의 '그라우뷘덴(Graubunden)' 응용과학대학교의 연구팀이 108일 9시간 걸려 계산한 것이다. 그때까지의 기록인 50조 자리보다 단숨에 약 13조 자리나 기록을 늘렸다. 앞으로도 계속 기록을 갱신할 것으로 보인다.
현재는 π의 근삿값 계산은 슈퍼컴퓨터의 성능을 평가하는 기준이 되었다. 또 π값 계산에서 축적된 지식이나 노하우는 '유체 역학(Fluid Mechanics)'의 시뮬레이션 등 여러 분야에서 활용되고 있다.
반응형7. π와 소수는 연결되어 있었다.
7-1. 바젤 문제
1644년에는 1/12+1/22+1/32+1/42+1/52+.....이 얼마에 수렴하느냐 하는 문제가 제기되었다. 이 문제에 도전한 사람이 스위스의 수학자 가문인 베르누이 가문이었다. 이 문제는 스위스 '바젤(Basel)'에서 고안되었기 때문에 '바젤 문제(Basel Problem)'라고 한다. 그러나 아쉽게도 베르누이 가문은 이 문제를 풀 수 없었다.
1735년에 이 문제를 해결한 사람은 당시 아직 무명이었던 스위스의 천재 수학자 '레온하르트 오일러(Leonhard Euler, 1707~1783)'이었다. '레온하르트 오일러'는 삼각함수 sin의 무한급수를 사용함으로써 '바젤 문제'의 해가 π2/6임을 유도했다. 놀랍게도 여기서도 π가 등장했다. 이 식을 '오일러 급수(Euler Series)'라고 한다.
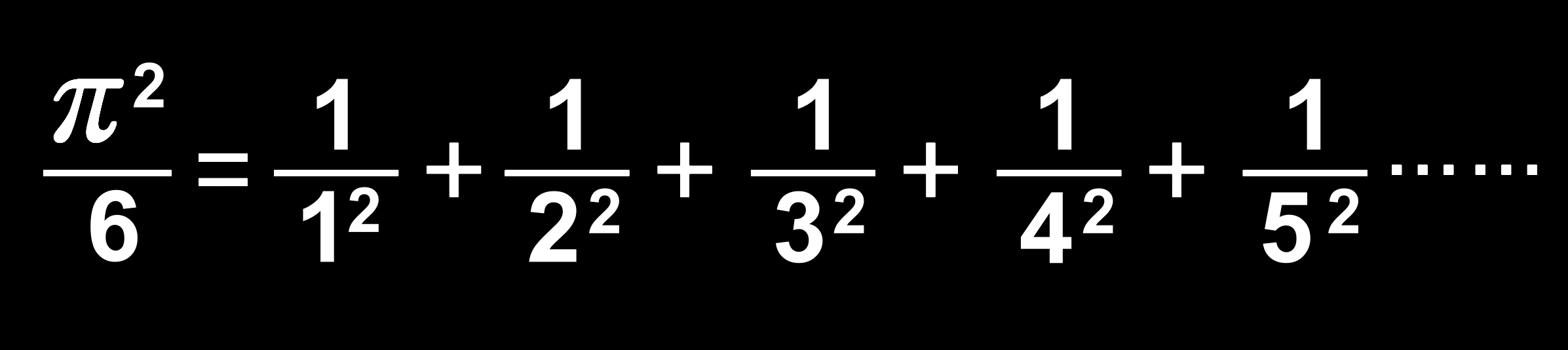
오일러 급수(바젤 문제의 해) 7-2. π는 모든 소수가 들어 있는 식으로 나타낼 수 있다.
오일러의 뛰어남은 여기에 머물지 않았다. 놀랍게도 '바젤 문제의 해'인 '오일러 급수'를 변형하면 π를 모든 소수를 사용한 식으로 나타낼 수 있음도 발견했다. '소수(Prime Number)'란 1과 그 수 자체 이외에 약수를 갖지 않는 자연수를 말한다. 2, 3, 5, 7, 9, 11, 13......처럼 무한히 존재하는 것이 알려져 있다. 그러나 그 출현 방식의 규칙성은 알려져 있지 않으며, 수학에서의 가장 중요한 과제의 하나로 생각되고 있다. '오일러'는 소수의 출현 방식에 대해 깊이 고찰해 '소수의 출현 방식에는 반드시 뭔가 규칙성이 있을 것'이라는 강한 신념을 가지고 있었다. 그런 '오일러'가 유도해낸 것이 아래에 제시한 식이다. 이 식에는 무한하게 존재하는 모든 소수가 들어 있다. 놀랍게도 원주율 π와 모든 소수는 연결되어 있었던 것이다.
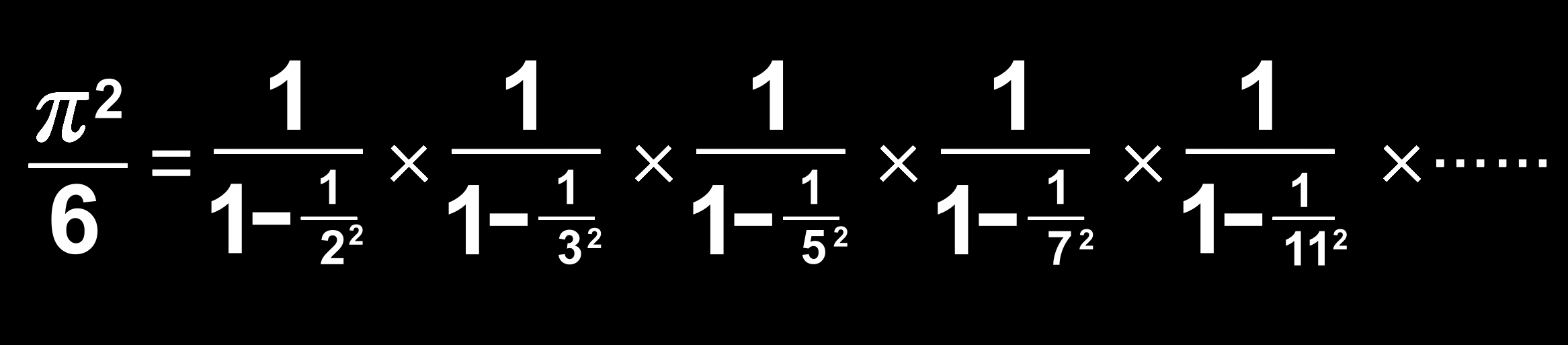
'오일러 급수'의 변형 7-3. '제타 함수'와 '리만 가설'
바젤 문제는 1/1n+1/2n+1/3n+1/4n+......이라는 식에 n=2를 대입한 것이라고 생각할 수도 있다. '오일러'는 이 식에 대해 더욱 고찰했다. 그리고 이 식의 n에 들어가는 수를 '복소수'로 확장해 '제타 함수(Zeta Function)'라는 이름을 붙인 사람이 독일의 수학자 '베른하르트 리만(Bernhard Riemann, 1826~1866)'이다.
1859년 '리만'은 '제타 함수'에 관한 어떤 중요한 가설을 제창했다. 그것은 바로 수학에서 가장 중요한 가설이라는 '리만 가설(Riemann Hypothesis)'이다. '리만 가설'이란 소수의 출현 방식의 규칙성에 관한 가설이다. '리만 가설'이 증명되면 소수의 출현 방식을 정확하게 알 수 있게 되기 때문에, 많은 수학자가 도전하고 있다. 그러나 '리만 가설'이 발표되고 지금까지 해결의 실마리조차 발견되지 않았다.
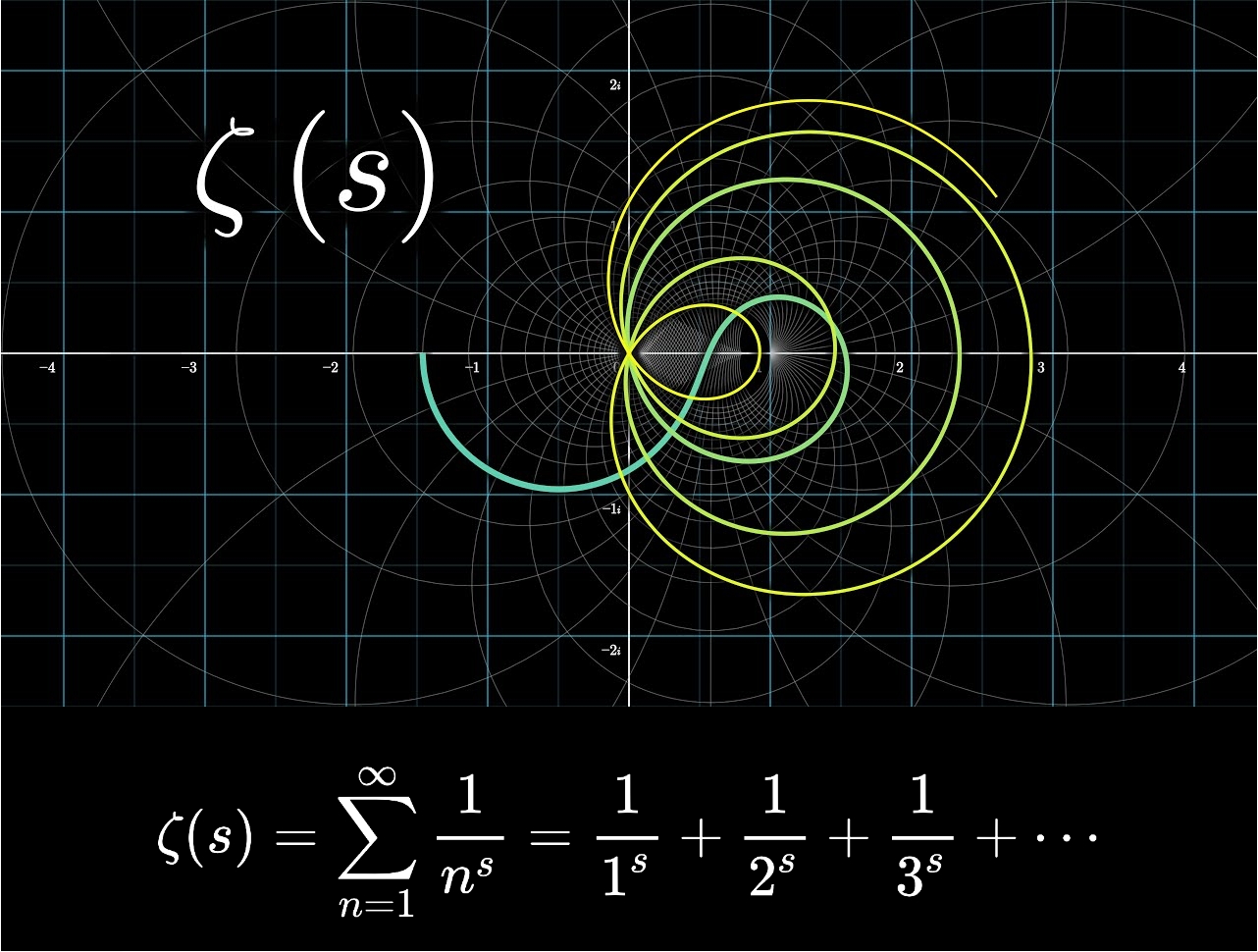
제타 함수(Zeta Function) 7-4. 오일러의 등식
마지막으로 '세상에서 가장 아름다운 식'으로 불리는 '오일러의 등식'을 소개한다. '오일러의 등식(Euler's Identity)'에는 'e', 'i', 'π', '1', '0'이라는 5개의 문자가 들어간다. 'e(자연 상수)', 'i(복소수)', 'π(파이)'는 각각 전혀 다른 배경을 가지고 있다.
- e(자연 상수): 수학계에서 가장 자주 등장하는 상수로, 예금의 이자 계산에서 생겼다.
- i(복소수): 2제곱하면 -1이 되는 복소수로, 방정식의 해를 찾는 중에 태어난 '실수'가 아닌 '허수'이다.
- π(파이): 원이라는 기하학적인 도형의 길이의 비 (원둘레/지름)
- 1: 가장 작은 자연수
- 0: '무(無)'를 나타내는 수
오일러의 등식에는 그 바탕이 되는 'eix=cos x + i sin x'라는 식이 있다. 이것을 '오일러의 공식'이라고 하며, 이 식에 x=π를 대입하면 간단히 '오일러의 등식'을 유도할 수 있다. '오일러의 공식'은 자연의 메커니즘을 해명하는 데 없어서는 안 될 식이 되었다. 미국의 물리학자 '리처드 파인만(1918~1988)'이 '오일러의 공식'을 두고 '인류의 더없이 중요한 보물'이라고 표현했을 정도이다.
'오일러의 공식'은 1748년에 '오일러'가 출판한 '무한 해석 개론'에서 발표되었다. '오일러의 공식' 및 '오일러의 등식'은 무한급수, 삼각 함수, 미분, 적분, 지수함수를 써서 유도할 수 있다. 이것은 '오일러의 등식'이 '고대 이집트', '고대 바빌로니아 시대' 이래 인류가 수천 년 동안 쌓아 온 수학의 오랜 역사 가운데 하나의 도달점임을 의미한다.
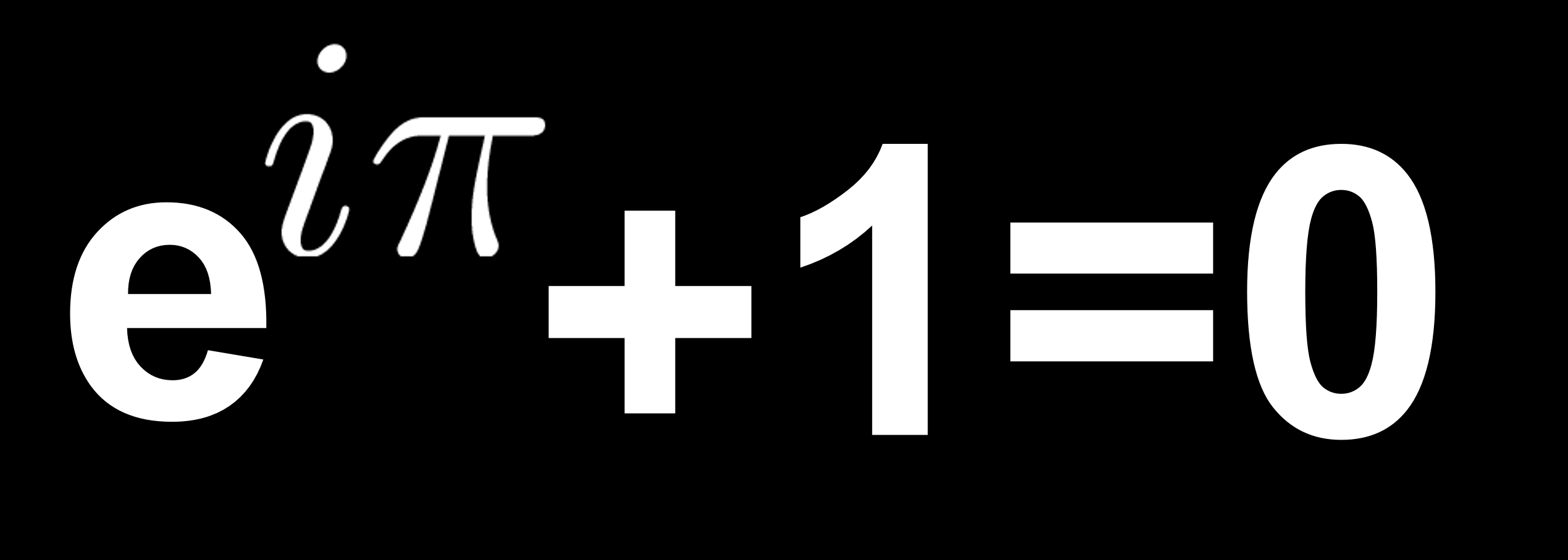
오일러의 등식(Euler's Identity)