'4색 정리(Four Color Theorem)'란 '지도에서 이웃한 영역이 다른 색깔이 되도록 칠하기 위해서는 4색이면 충분하다.'는 정리이다. 단 '이웃'한다는 것은 경계선을 공유함을 나타내고, 경계선의 교점에서 접하는 것은 이웃하지 않는 것으로 간주한다. 정리의 내용 자체는 간단히 이해할 수 있지만 정말 맞는 것일까?
0. 목차
- '정리'란 무엇인가?
- 4색 문제
- '4색 문제'를 풀었다고 주장한 '프랜시스 거스리'
- 지도를 '점'과 '선'으로 생각해 보자.
- 4색 문제가 증명되었다.

1. '정리'란 무엇인가?
'4색 정리(Four Color Theorem)'를 설명하기 전에 '정리(定理, Theorem)'의 의미에 대해 알아보자. '정리'와 비슷한 의미로 '공리'와 '공식'이라는 용어도 있다. '공리(Axiom)'란 수학의 토대가 되는 가정을 말한다. 예를 들어 '2개의 점이 주어졌을 때 그 2점을 지나는 직선을 그을 수 있다.'는 것은 유클리드 기하학에서의 공리다. 그리고 공리를 전제로 도출된 사실을 '정리(Theorem)'라고 하며, 특히 수식으로 나타낼 수 있는 정리를 '공식(Formula)'이라고 한다.
수학에서는 '○○ 문제'나 '●● 추측'이라는 말을 많이 듣게 된다. 이것들은 아직 증명되지 않은 정리나 공식을 가리킨다. 미국의 '클레이 수학 연구소(CMI: Clay Mathematics Institute)'가 100만 달러의 현상금을 건 '밀레니엄 현상 문제(밀레니엄 7대 난제)'가 유명하다. 7개 모두 미해결 문제였는데, 그 가운데 '푸앵카레 추측(Poincare Conjecture)'은 해결되었다. 그래서 '4색 정리'가 증명되기 전에는 '4색 문제'였지만, 이제는 '4색 정리'라고 불린다. 정리나 문제 가운데, 답이 '옳은지 옳지 않은지(진위)' 어느 쪽으로든 결정된 것을 '명제'라고 한다.
2. 4색 문제
'4색 문제'에서는 평면에 그려진 지도의 색 분할을 생각해 보자. 현실 세계의 지도도 좋고 자신이 생각한 지도도 좋다. 종이와 색연필을 준비해 마음대로 지도를 만들고 색연필로 칠해보자. 이때 이웃한 영역은 다른 색을 칠해야 한다. 또 점으로 접하는 영역은 이웃한 것으로 간주하지 않는다. 예를 들어 미국 지도에서 경계선이 십자 형태로 교차하는 곳에서는 대각 방향의 주끼리는 같은 색깔이어도 된다. 이제 자신이 만든 지도를 4색으로 구분해 보자. 만약 5색 이상을 사용했다면, 4색 정리가 잘못된 것이 아니라 색깔을 칠한 사람이 잘못한 것이다.
또 평면이 아니라 '토러스(Torus, 도넛처럼 구멍이 1개 있는 입체)'의 표면에 그려진 지도를 색 구분하기 위해서는 최대 7가지 색이 필요하다. 이 정리는 1890년에 영국의 수학자 '퍼시 존 헤이우드(1861~1955)'가 증명했다. 이처럼 구멍이 뚫린 지도는 4색으로 구분할 수 있다고 단정할 수 있다. 단, 지구처럼 구멍이 뚫리지 않은 입체의 표면에 그려진 지도는 4색으로 구분할 수 있다.

| 표면 | 구분을 위해 필요한 최소한의 색의 수 |
| 2차원 평면 | 4 |
| '구(Sphere)'의 표면 | 4 |
| '토러스(Torus)' 표면 | 7 |
3. '4색 문제'를 풀었다고 주장한 '프랜시스 거스리'
'4색 문제'는 1852년, 당시 학생으로 나중에 영국의 수학자가 된 '프랜시스 거스리(Francis Guthrie, 1831~1899)'가 주장했다. 그의 동생이며 나중에 물리학자가 된 '프레더릭 거스리(1833~1886)'는 그 말을 듣고 영국의 수학자인 '오거스터스 드모르간(Augustus De Morgan, 1806~1871)'에게 4색 문제가 옳은지 물었다. 이 질문을 받은 '오거스터스 드모르간'은 아일랜드의 수학자이며 물리학자인 '윌리엄 로언 해밀턴(William Rowan Hamilton, 1804~1865)'에게 편지를 썼다. 그러나 '윌리엄 해밀턴'의 반응은 쌀쌀했다. 결국 '오거스터스 드모르간'을 포함한 몇 명의 수학자만이 관심을 기울이는 상황이 되었다. 그 후 '오거스터스 드모르간'은 문제를 증명하지 못하고, 1871년에 사망해 '4색 문제'는 잠시 휴면 상태에 들어갔다.
시간이 흘러 1878년, 영국의 수학자이며 변호사이기도 했던 '아서 케일리(Arthur Cayley, 1821~1895)'가 이 문제를 영국 수학회에 다시 제기하면서 빛을 보게 되었다. 이때 영국의 아마추어 수학자였던 '알프레드 브레이 켐프(Alfred Bray Kempe, 1849~1922)'는 이 이야기를 듣고 바로 '4색 문제'의 증명에 나섰다. '켐프'는 '켐프 사슬(Kempe Chain)'이라는 독창척인 기법을 고안하고, 이 기법을 사용해 4색 문제를 증명하는 데 성공했다고 주장했다. 그 논문은 다음 해인 1908년에 '미국 수학 저널'에 게재되었다. 모두가 그 증명이 옳다고 믿었지만, 사실 그의 증명에는 한 가지 중대한 실수가 있었다. 이 실수를 그 누구도 발견하지 못했고, 10년 동안 '켐프'의 증명은 옳다고 받아들여졌다.
'켐프'의 증명 실수는 1890년에 영국의 수학자인 '퍼시 존 헤이우드(1861~1955)'가 지적했다. 그는 '토러스(Torus, 도넛처럼 구멍이 1개 있는 입체)'에 그려진 7가지 색으로 구분됨을 증명한 인물이다. '헤이우드'는 '켐프'의 증명이 틀렸음을 증명했지만, 4색 문제 그 자체를 증명하지는 못했다. 그 대신, 평면이나 구면에 그려진 지도는 적어도 '5색'으로 구분할 수 있음을 밝혔다. '헤이우드'의 지적에서 주목해야 할 점은, 모두가 옳다고 믿고 있던 증명이 틀렸다는 사실이다. 그 후 '4색 문제'는 매우 어려운 문제라는 인식이 퍼지기 시작했으며, 이후 100년 가까운 세월 동안 수학자들을 괴롭혔다.
4. 지도를 '점'과 '선'으로 생각해 보자.
사실 4색 문제를 생각할 때 효과적인 방법이 있다. 먼저 경계선으로 둘러싸인 영역에 각각 '점'을 찍고, 이웃 영역에 놓인 점끼리 선으로 연결한다. 이렇게 하면 지도로 표현했을 때보다 눈에 잘 들어온다. 이처럼 점과 선만을 이용해 다양한 '연계'를 표현하는 이론을 '그래프 이론'이라고 하며, 조합 문제를 간결하게 기술하는 데 효과적이다. 그래프에 색을 칠할 수는 없기 때문에 점에 숫자 1, 2, 3, 4를 붙이는 작업을 한다. 선으로 연결된 점은 이웃하고 있음을 의미하기 때문에 같은 숫자를 붙일 수 없다. 이처럼 4색 문제는 '평면에 그려진 그래프의 점에 숫자를 붙이는 것을 생각할 때, 선으로 연결된 점끼리 숫자가 다르게 하기 위해서는 4개의 숫자만으로 충분한가?'라는 명제로 바꿀 수 있다.
그리고 또 한 가지, '4색 문제'를 생각할 때 필수적인 정리를 소개한다. 스위스의 유명한 수학자인 레온하르트 오일러(Leonhard Euler, 1707~1783)'가 제창한 '오일러의 다면체 정리(Euler's Theorem)'이다. 구멍이 뚫리지 않은 다면체를 생각할 때, 꼭짓점의 수와 면의 수를 합한 것에서 변의 수를 빼면 반드시 2가 된다는 정리이다. 예를 들어 주사위와 같은 정육면체의 꼭짓점의 수는 9, 면의 수는 6, 변의 수는 12이므로, 8+6-12=2가 되어 '오일러의 다면체 정리가 성립한다.
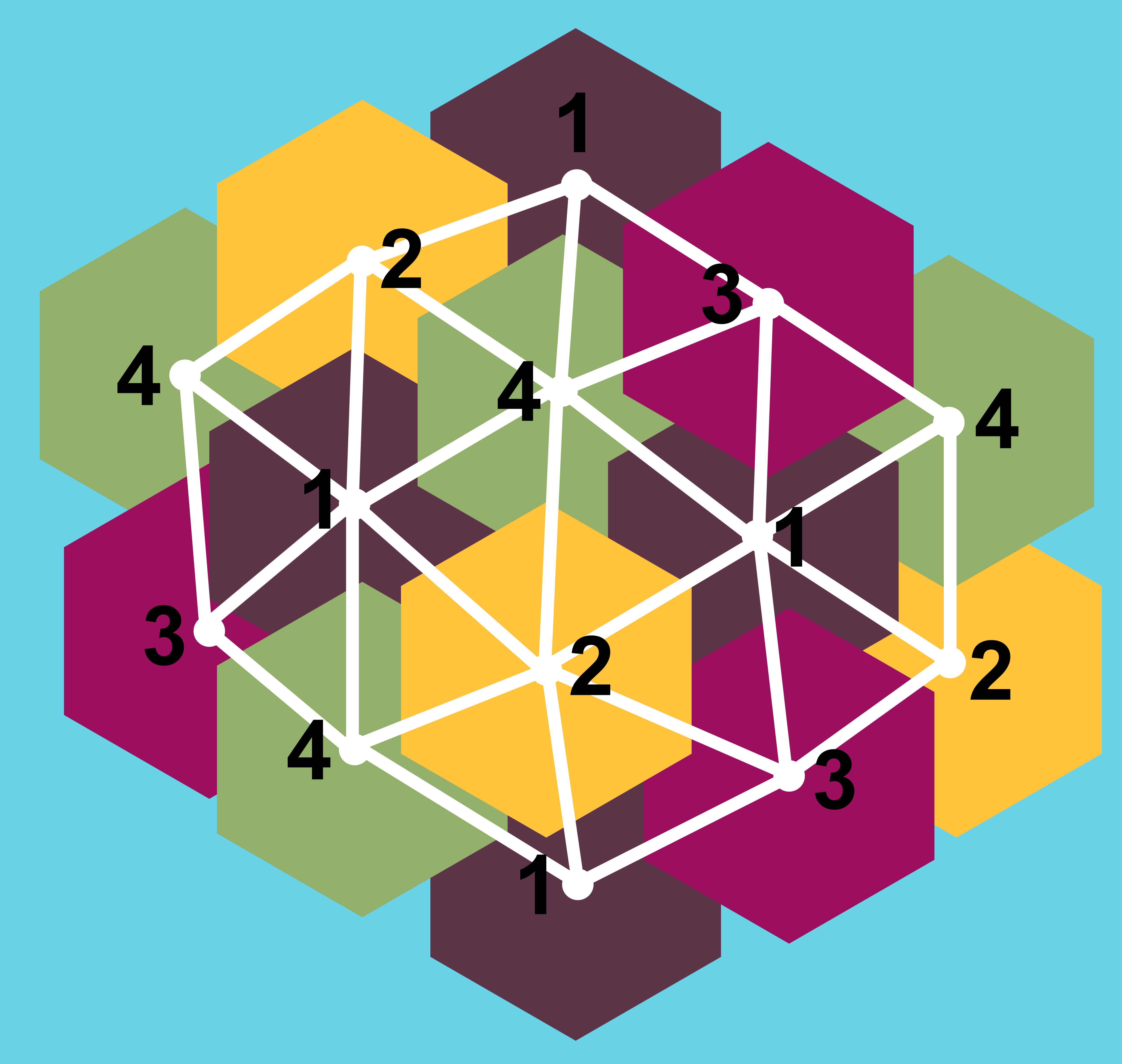
그런데 사실 '오일러의 다면체 정리(Euler's Theorem )'는 평면 지도에도 똑같이 적용할 수 있다. 결국 평면 지도를 점과 선을 이용해 그린 그래프에도 성립한다. 이 경우, '점의 수'와 '선으로 둘러싸인 영역의 수'를 더한 것에서 '선의 수'를 빼면 2가 된다. 아래의 그래프의 경우 '점의 수'가 14, '선으로 둘러싸인 영역의 수'가 17(바깥쪽 영역도 하나로 센다), '선의 수'가 29이므로, 14+17-29=2가 성립한다.
5. 4색 문제가 증명되었다.
5-1. 4색 문제를 해결하기 위한 새로운 접근 방식
오일러의 다면체 정리'에 근거한 기법을 통해, 1940년에는 35개 이하의 나라로 이루어진 세계 지도는 4색으로 구분할 수 있음이 밝혀졌다. 그런데 증명하고 싶은 것은 어떤 세계 지도이든 4색으로 구분할 수 있느냐는 점이다. 36개국, 37개국, 38개국... 처럼 하나씩 확인해 나간다고 해도 증명은 끝나지 않을 것이다. 왜냐하면 나라의 수에 제한이 없기 때문이다.
여기에서 '4색 문제는 성립하지 않는다.'고 가정해 보자. 만약 '4색 문제'가 성립하지 않는다면, 절대로 4색으로 이웃한 영역을 구분할 수 없는 지도가 존재하게 된다. 그런 가정을 바탕으로 4색 문제를 생각해 보면, 가정과 모순되는 결과가 도출되는 경우가 있다. 만일 모순이 생기면 최초의 가정인 '4색 문제는 성립하지 않는다'는 잘못된 셈이다. 이처럼 어떤 명제를 증명하기 위해 명제가 성립하지 않는다고 가정하고, 그 모순을 도출함으로써 명제가 성립하는 방법을 '배리법(背理法)'이라고 한다.
미국의 수학자인 '케네스 아펠(Kenneth Ira Appel, 1923~2013)'과 독일의 수학자인 '볼프강 하켄(Wolfgang Haken, 1928~2022)'은 '배리법'을 바탕으로 다양한 그래프를 조사했다. 그러나 이 작업에는 방대한 시간이 소요됨을 알았기 때문에 컴퓨터를 사용하기로 했다. 두 사람은 그래프의 패턴을 수작업으로 조사한 다음, 당시의 최신 기기를 포함한 3대의 컴퓨터를 사용해 검증에 나섰다. 계산 시간은 총 1200시간을 넘었으며, 계산 결과가 기록된 인쇄물을 쌓아 올리면 1.2m나 되었다.
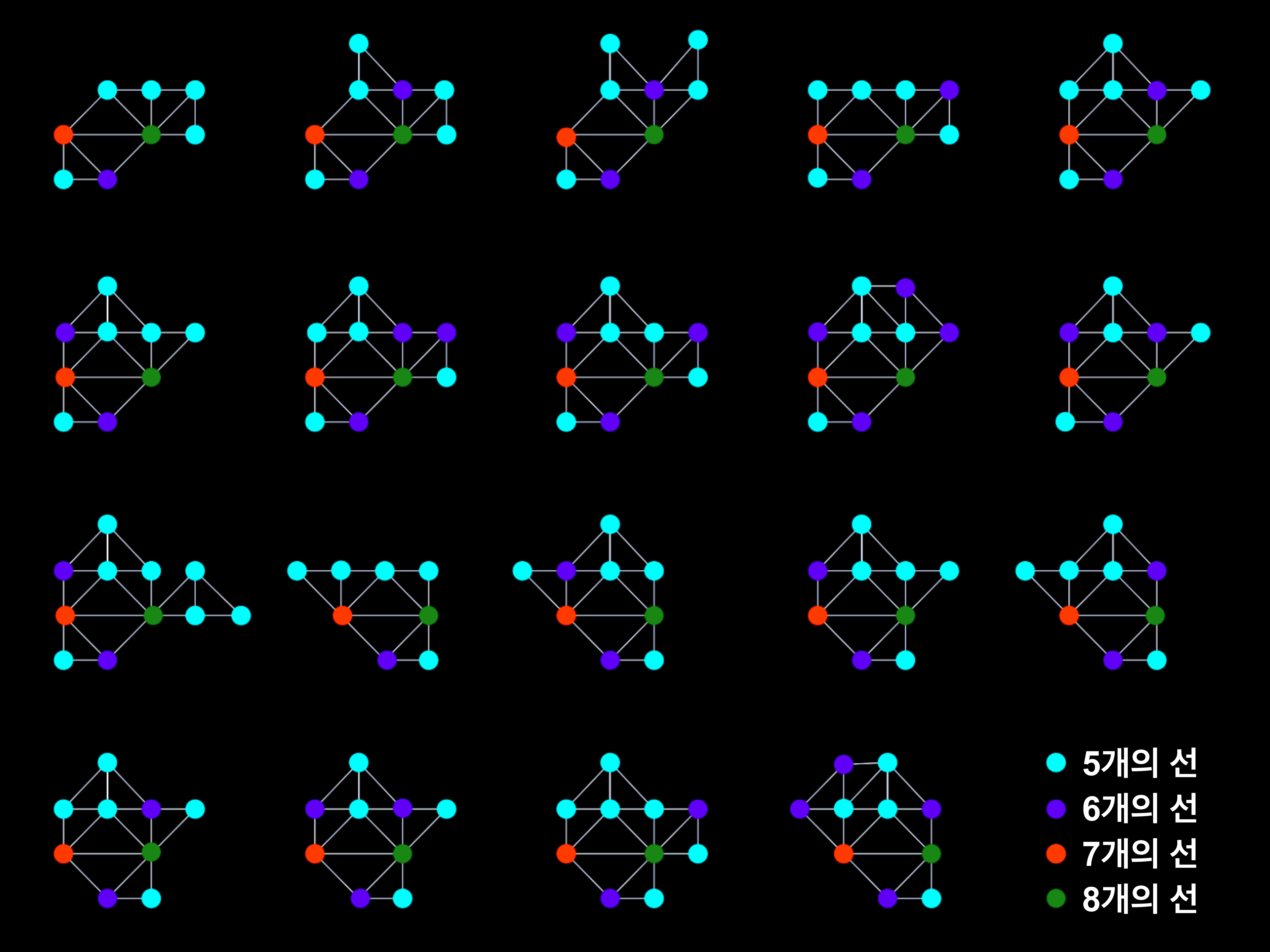
아래에 제시한 그래프는 4색 정리의 증명으로 조사된 그래프의 예이다. 이들 그래프는 퍼즐 조각과 같은 것으로 그 어떤 그래프에 포함된 일부분이다. 빨간색 점은 '선을 5개 가지고 있음(이웃 나라가 5개 있음)'을 나타낸다. 대부분의 점에서 선의 수가 부족하지만, 원래 그래프에 끼워 넣어 선의 수를 채우게 된다. '케네스 아펠(Kenneth Ira Appel)'과 '볼프강 하켄(Wolfgang Haken)'은 컴퓨터를 사용해 이런 그래프를 2000개 이상 조사했다.
5-2. '증명'이란 무엇인가?
이 계산 결과가 올바르면 '4색 문제는 성립하지 않는다'는 가정과 모순되어 '4색 문제'를 증명할 수 있었다. 이 계산 결과는 다른 수학자에 의해 올바름이 검증되어 마침내 '4색 문제'는 증명되었다. '프랜시스 거스리(Francis Guthrie)'가 '4색 문제'를 제기한 지 124년 후인 1976년의 일이었다.
그러나 방대한 양의 계산을 컴퓨터에 맡기고, 그것을 바탕으로 증명하는 방식에 대해 많은 비판이 쏟아졌다. 수학자에게 '증명(Proof)'이란 인간의 손으로 우아하게 이루어지는 것이라고 여겨졌기 때문이다. 이 증명 방법에 관한 논쟁은 철학 분야로 파급되어 '증명이란 무엇인가?'라는 질문을 인류에게 남겼다. '4색 문제'는 증명되어 정식으로 '4색 정리'로 불리게 되었다. 하지만 컴퓨터를 사용하지 않고 종이와 연필만을 사용한 우아한 증명은 아직 성공하지 못했다. 그런 의미에서는 일종의 미해결 문제라고 해도 좋을 것이다.
현재 4색 정리는 휴대전화의 기지국 영역 배치에 응용되고 있다. 같은 주파수를 가진 기지국들이 인접하지 않도록 주파수의 '색 구분'을 하고 있다. 언뜻 우리 생활과 아무런 관련이 없다고 생각되는 정리도 우리 생활 주변에서 활약하고 있는 것이다.