고대 그리스의 철학자 '플라톤(Plato)'은 '정다각형(Regular Polygon)'만으로 이루어진 입체인 '정다면체(Regular Polyhedron)'를 신성시했다. 그가 주목한 5가지 정다면체, 즉 '정사면체', '정육면체(입방체)', '정팔면체', '정이십면체', '정이십면체'를 통틀어 '플라톤 입체(Platonic Solid)'라고 한다. 정다면체는 '황금비'를 갖고 있다거나 '구(Sphere)'에 꽉 맞게 들어가는 등의 불가사의한 성질을 가지고 있어, 기원전부터 사람들을 매혹시켜왔다.
0. 목차
- 플라톤 입체 (Platonic Solid)
- 외접구와 내접구
- 쌍대 (Dual)
- 사면체 타일 정리
- 황금비 (Golden Ratio)
- 지오데식 돔 (Geodesic Dome)
- 아르키메데스 입체
- 공간을 꽉 채우는 방법

1. 플라톤 입체 (Platonic Solid)
납작한 면으로 둘러싸인 입체를 '다면체(Polyhedron)'라고 한다. 예컨대 정육면체나 직육면체, 삼각기둥 등이 다면체이다. 원기둥처럼 구부러진 면이 포함되는 입체는 다면체가 아니다. '정삼각형'이나 '정사각형'처럼 변의 길이와 각의 크기가 모두 같은 다각형을 정다각형이라고 한다. 그리고 모든 면이 똑같은 정다각형으로 이루어진 다면체를 '정다면체'라고 한다. 정확하게는 '모든 꼭짓점에 모여 있는 면이나 변의 수가 같은 것', '움푹 팬 부분이 없을 것'도 정다면체가 되기 위한 필요조건이다.
정다면체는 '정사면체(Regular Polyhedron)', '정육면체(Regular Hexahedron, Cube)', '정팔면체(Octahedron)', '정십이면체(Regular Dodecahedron)', '정이십면체(Icosahedron)' 단 5개만 존재한다. 정다면체가 5종류밖에 존재하지 않는 것을 증명한 사람은 '플라톤(Plato)'이 아니라 그의 친구인 수학자 '테아이테토스(Theaitetos)'라는 이야기도 있다. 이 5개의 정다면체는 고대 그리스의 철학자 '플라톤(기원전 427~347)'의 이름을 따 '플라톤 입체'라고도 한다. 플라톤은 그의 책 '티마이오스(Timaios, 대화편)'에서 이들 정다면체를 사용해 만물을 구성하는 원소의 성질을 설명할 수 있다고 썼다. 현재 말하는 원자가 각각의 정다면체 모양을 하고 있다고 생각한 것이다. 당시 만물은 흙, 공기, 불, 물의 4종류의 원소로 구성되어 있다고 생각했다. 플라톤은 흙의 모양에 정육면체를 할당했다. 4종류의 원소 가운데 가장 안정되고 움직이기 어려운 성질을 가진 흙에는 안정된 밑면을 가진 '정육면체'가 어울린다고 생각했기 때문이다. 정십이면체에 대해서는 '티마이오스(Timaios)'에 대응하는 원소가 제시되어 있지 않다. 그러나 우주에 존재하는 미지의 제5원소 '에테르'에 대응한다고 생각했다는 설이 있다.
| 플라톤이 생각한 '정다면체'와 '원소'의 관계 | |
| 정사면체(Regular Polyhedron) | 불 |
| 정육면체(Regular Hexahedron, Cube) | 흙 |
| 정팔면체(Octahedron) | 공기 |
| 정십이면체(Regular Dodecahedron) | 에테르? |
| 정이십면체정이십면체(Icosahedron) | 물 |
1-2. 플라톤 입체는 왜 5종류밖에 없을까?
입체를 만들기 위해서는 입체의 꼭짓점 1개의 주위로 3개 이상이 다각형이 모여 있어야만 한다. 2개만으로는 입체가 되지 않기 때문이다. 아래의 정육면체의 전개도를 보자. 전개도 1에서 만약 노란색 꼭짓점의 왼쪽 아래에 정사각형이 또 하나 더해지면 어떻게 될까? 꼭짓점 주위가 평면이 되어버려, 즉 꼭짓점에 모이는 각의 합이 360˚가 되어버려 접히지 않게 된다. 이 말은 입체가 될 수 없다는 말이다. 바꿔 말하면 입체를 만들기 위해서는 하나의 꼭짓점에 모이는 각의 합이 360˚ 미만이어야 한다.
이제 조건을 만족하는 정다각형의 배열 방법을 따져 보자. 하나의 꼭짓점에 정다각형을 3개 이상 모으고 각의 합이 360˚ 미만이 되는 배열 방법은 몇 가지 있을까? 내각이 90˚인 정사각형은 1가지뿐이다. 내각이 60˚인 정삼각형은 3가지가 있다. 내각이 108˚인 정오각형은 1가지뿐이다. 정육각형이나 그보다 각이 많은 정다각형은 조건을 만족시킬 수 없다. 즉 조건을 만족하는 입체는 5가지밖에 없다. 이 5가지 배열 방법으로 하나의 꼭짓점에 정다각형을 모으고 각각 입체를 만들면 모든 꼭짓점에 모이는 면과 변의 수가 같은 정다면체를 만들 수 있다. 이것이 정다면체가 5종류밖에 없는 이유다.

2. 외접구와 내접구
5종류의 정다면체는 정사면체처럼 뾰족한 것에서부터 정십이면체처럼 공에 가까운 모양도 있다. 어떤 모양이든 정다면체는 '구(Sphere)' 안에 꼭 맞게 들어간다. 모든 꼭짓점이 구에 접히는 것이다. 이렇게 정다면체의 바깥쪽에 접하는 구를 '외접구(Circumscribed Sphere)'라고 한다. 중심에서 각 꼭짓점까지의 거리가 모두 같다는 정다면체의 특징을 나타낸다고 할 수 있다. 정다면체와 구의 불가사의한 관계는 그뿐만이 아니다. 정다면체 안에도 구가 들어간다. 이처럼 정다면체의 안쪽에 접하는 구를 '내접구(Inscribed Sphere)'라고 한다. '내접구'는 정다면체의 면 중심과 구가 접한다. 이는 중심에서 각면까지의 거리가 모두 같다는 정다면체의 특징 때문에 가능한 일이다.

2-1. 태양계 행성의 궤도를 정다면체로 설명할 수 있다?
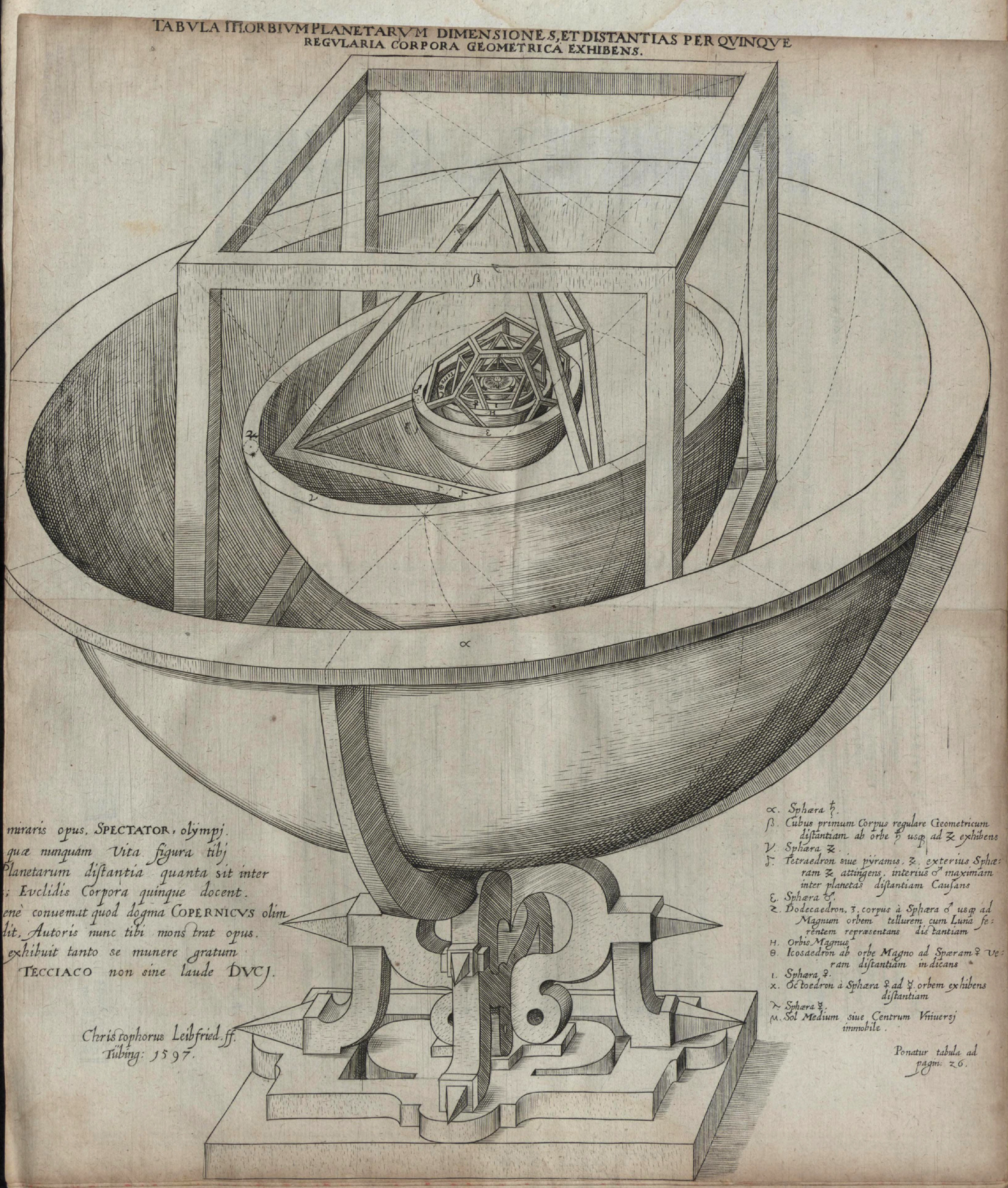
독일의 천문학자 '요하네스 케플러(Johannes Kepler, 1571~1630)'는 정다면체의 이런 성질에 주목했다. 정다면체와 그것에 접하는 구를 사용해 태양계 행성의 궤도를 설명할 수 있으리라 생각한 것이다. '요하네스 케플러'는 당시 알려져 있던 6개 행성 수성, 금성, 지구, 화성, 목성, 토성의 궤도를 구면 위에다 그렸다. 그리고 궤도를 그린 6개 구 사이에 5개의 정다면체를 끼워 넣어 태양계 모델을 만들었다. '플라톤'과 마찬가지로 '요하네스 케플러'도 정다면체의 신비한 성질을 자연계 현상을 설명하는 데 사용할 수 있으리라 생각했던 것이다. 그러나 정다면체를 사용한 이 모델은 나중에 틀렸음이 판명되었다.
정다면체를 사용한 태양계 모델은 '요하네스 케플러'가 1596년 발표한 '우주의 신비'에 실려 있다. 가장 바깥쪽의 구면 위를 토성이 돌고, 그 구의 안쪽을 정육면체가 접한다. 그 정육면체의 안쪽에 접히는 구면 위를 목성이 돌고, 다시 그 구의 안쪽에 정사면체가 접한다. 이런 식으로 6개 행성의 궤도가 포함된 '구(Sphere)'와 5개의 정다면체를 조합시켰다. 그러나 이 태양계 모델은 당시의 정밀한 천문 관측 데이터와 일치하지 않았다. 행성의 타원 궤도는 구면 위에서 어긋나 버렸기 때문이다. 그래서 케플러는 이 모델을 수정했고, 올바른 법칙에 이르렀다.
3. 쌍대 (Dual)
정다면체 각 면의 중심을 직선으로 연결하면 새로운 입체가 나타나는데, 불가사의하게 그 입체도 정다면체가 된다.
- 정사면체 각면의 중심을 직선으로 연결하면 위아래가 바뀐 작은 정사면체가 나타난다.
- 정육면체 각 면의 중심을 직선으로 연결하면 작은 정팔면체가 나타난다.
- 정팔면체 각 면의 중심을 직선으로 연결하면 작은 정육면체가 나타난다.
- 정이십면체 각면의 중심을 직선으로 연결하면 작은 정십이면체가 나타난다.
- 정십이면체 각면의 중심을 직선으로 연결하면 작은 정이십면체가 나타난다.
이러한 관계성을 '쌍대(Dual)'라고 한다. '정사면체'는 자기 자신과 쌍대 관계에 있기 때문에 '자기 쌍대(Self-Dual)'라고 한다.
3-1. '면의 수'와 '꼭짓점의 수'가 바뀐다.
쌍대 관계가 생기는 배경에는 정다면체의 '면'과 '꼭짓점'의 수가 관계하고 있다. 아래의 표는 5개 정다면체의 면과 꼭짓점, 그리고 변의 수를 정리한 것이다. 정다면체 각 면의 중심을 직선으로 연결해 새로운 입체를 만들면, 면의 중심이 새로운 꼭짓점이 된다. 다시 말해 원래의 입체가 가진 면의 수가 새로 생긴 입체의 꼭짓점 수가 되는 것이다. 아래 표를 살펴보면 쌍대 관계에 있는 정육면체와 정팔면체에서는 한쪽 도형의 면 수와 다른 한쪽 도형의 꼭짓점 수가 같은 관계가 보이고, 정십이면체와 정이십면체에서도 한쪽 도형의 면수와 다른 한쪽 도형의 꼭짓점 수가 같은 관계가 보인다. 정사면체는 면의 수와 꼭짓점 수가 각각 4개로 같다. 그래서 면의 중심을 이어 생기는 입체도 정사면체가 되어, '자기쌍대(Self-Dual)'가 된다.
| - | 면의 수 | 꼭짓점 수 | 변의 수 |
| 정사면체 | 4 | 4 | 6 |
| 정육면체 | 6 | 8 | 12 |
| 정팔면체 | 8 | 6 | 12 |
| 정십이면체 | 12 | 20 | 30 |
| 정이십면체 | 20 | 12 | 30 |
4. 사면체 타일 정리
4개의 꼭짓점을 반드시 통과하고 여러 조각으로 뿔뿔이 흩어지지 않게 정사면체를 잘라 펼치면 1개의 전개도가 생긴다. 실은 이렇게 생긴 전개도에는 불가사의한 성질이 있다. 전개도가 어떤 모양이더라도 반드시 평면을 꽉 채울 수 있다. 어떤 도형을 빈틈없이 평면에 깔아 꽉 채우는 것을 '타일 깔기' 또는 '테셀레이션(Tessellation)'이라고 한다. '면을 꽉 채운다.'는 말은 틈새나 겹침이 생기지 않도록 해서 타일처럼 어떤 도형을 평면에 채우는 것이다. 꼭짓점 4개를 지나도록 잘라 펼치면, 어떤 모양으로 자르더라도, 어느 면의 팬 곳을 이웃한 면의 튀어나온 부분이 보충해 주는 그런 관계가 된다. 평면에 깔면 팬 곳을 보충해 원래의 정삼각형이 복원되는 것이다. 그 결과, 아래의 그림처럼 빈틈을 꽉 채울 수 있다. 정사면체를 자르고 펼쳐 평면을 꽉 채우는 여러 가지 모양을 만드는 방법은 일본의 수학자 '아키야마 진' 박사가 발견했기 때문에 '아키야마의 사면체 타일 정리'라고 한다.
일반적인 타일 모양이기도 한 정사각형의 경우, 평면을 꽉 채울 수 있다. 정육각형도 꽉 채우는 것이 가능하다. 한편, 정오각형은 틈새가 생겨 꽉 채울 수 없다. 평면을 꽉 채울 수 있는 정다각형은 '정삼각형', '정사각형', '정육각형'의 3가지뿐이다.
5. 황금비 (Golden Ratio)
5-1. '황금비'와 '황금수'
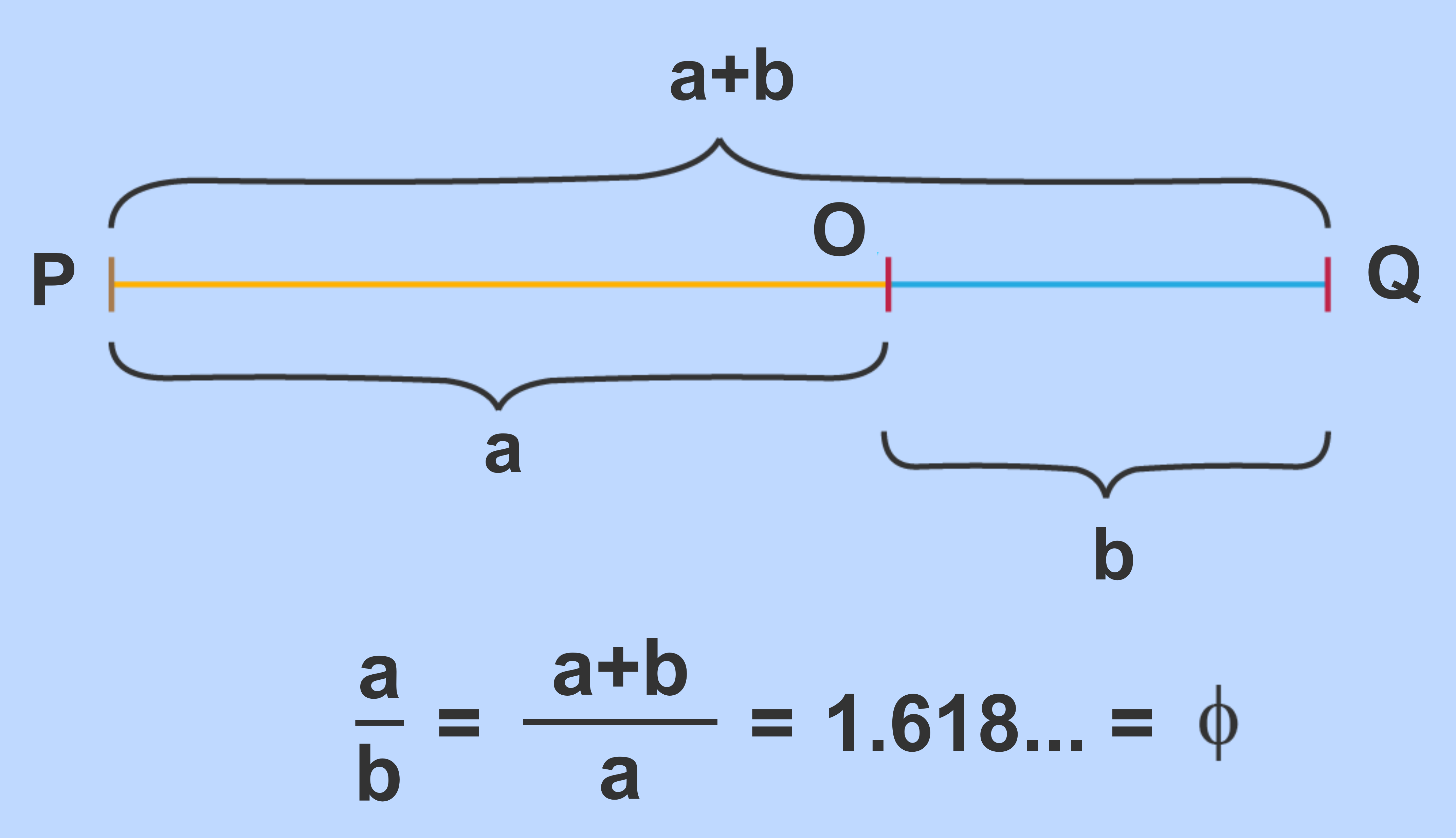
균형을 이룬 아름다운 비율인 '황금비'는 기원전의 고대 그리스 시대에도 이미 알려져 있었다. 고대 그리스의 수학자 '유클리드'는 그의 책 '원론'에서 '하나의 선분을 둘로 분할해 짧은 쪽과 긴 쪽의 길이의 비'와 '긴 쪽과 선분 전체 길이의 비' 가 같아질 때의 비를 '황금비(Golden Ratio)'라고 정의했다. 이 황금비의 비율을 수로 나타내면 1:1.168033......'이고 정확하게는 '(1+√5)÷2'이다. 이 '1.618033...'이라는 수를 '황금수(Golden Number)'라고 하며, 'φ(피)'라는 기호로 나타낸다.
5-2. '황금 직사각형'과 '황금 나선'
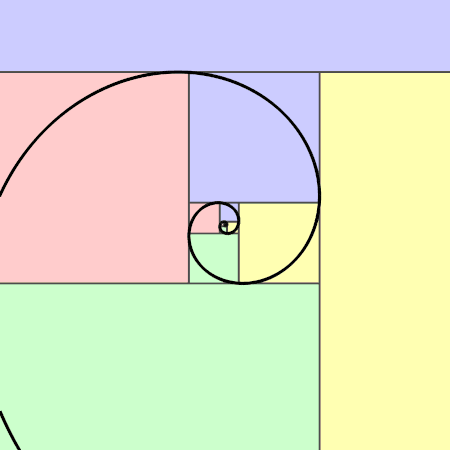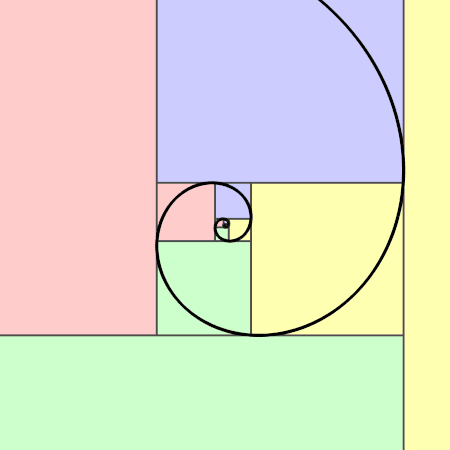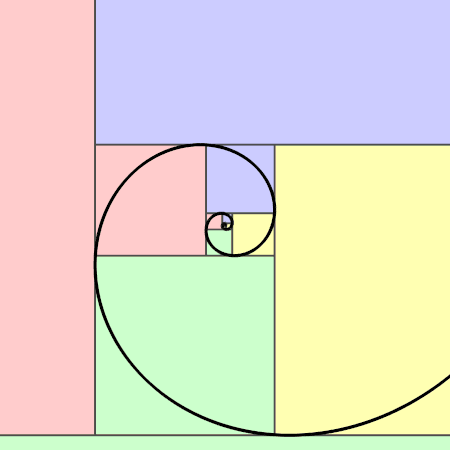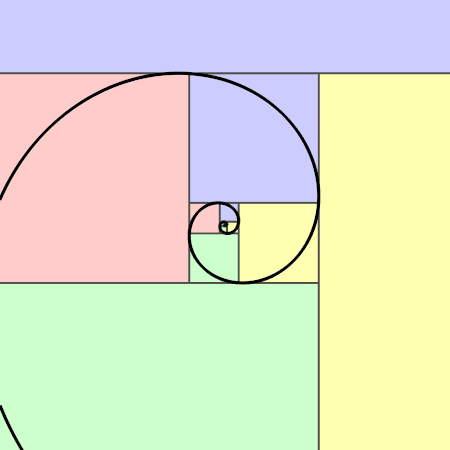
가로와 세로의 길이의 비가 '황금비(1:φ)'로 되어 있는 직사각형을 '황금 직사각형'이라 한다. 황금 직사각형 안에 선을 그어 정사각형을 만든다. 그러면 남은 직사각형도 황금 직사각형이 된다. 이것을 계속 반복하면 영원히 작은 황금 직사각형이 생긴다. 그리고 아래 그림처럼 정사각형 안에 그린 원호를 이으면 '황금 나선(Golden Spiral)'이 완성된다. 이것은 도형의 임의의 한 부분이 전체의 형태와 닮은 '프랙털(Fractal)'의 일종이다.
5-3. '정십이면체'와 '정이십면체'에 숨겨진 황금비
'프랙털 입체(Fractal Solid)'에도 불가사의한 황금비가 숨어 있다. 정이십면체의 마주 보는 변을 직선으로 연결하면 생기는 직사각형은 '황금 직사각형'이 된다. 또 '정십이면체'에서는 마주 보는 면의 중심을 직선으로 연결할 때 생기는 직사각형이 황금 직사각형이 된다. 또 '정십이면체'에서도 마주 보는 면의 중심을 직선으로 연결할 때 생기는 직사각형이 황금 직사각형이 된다.
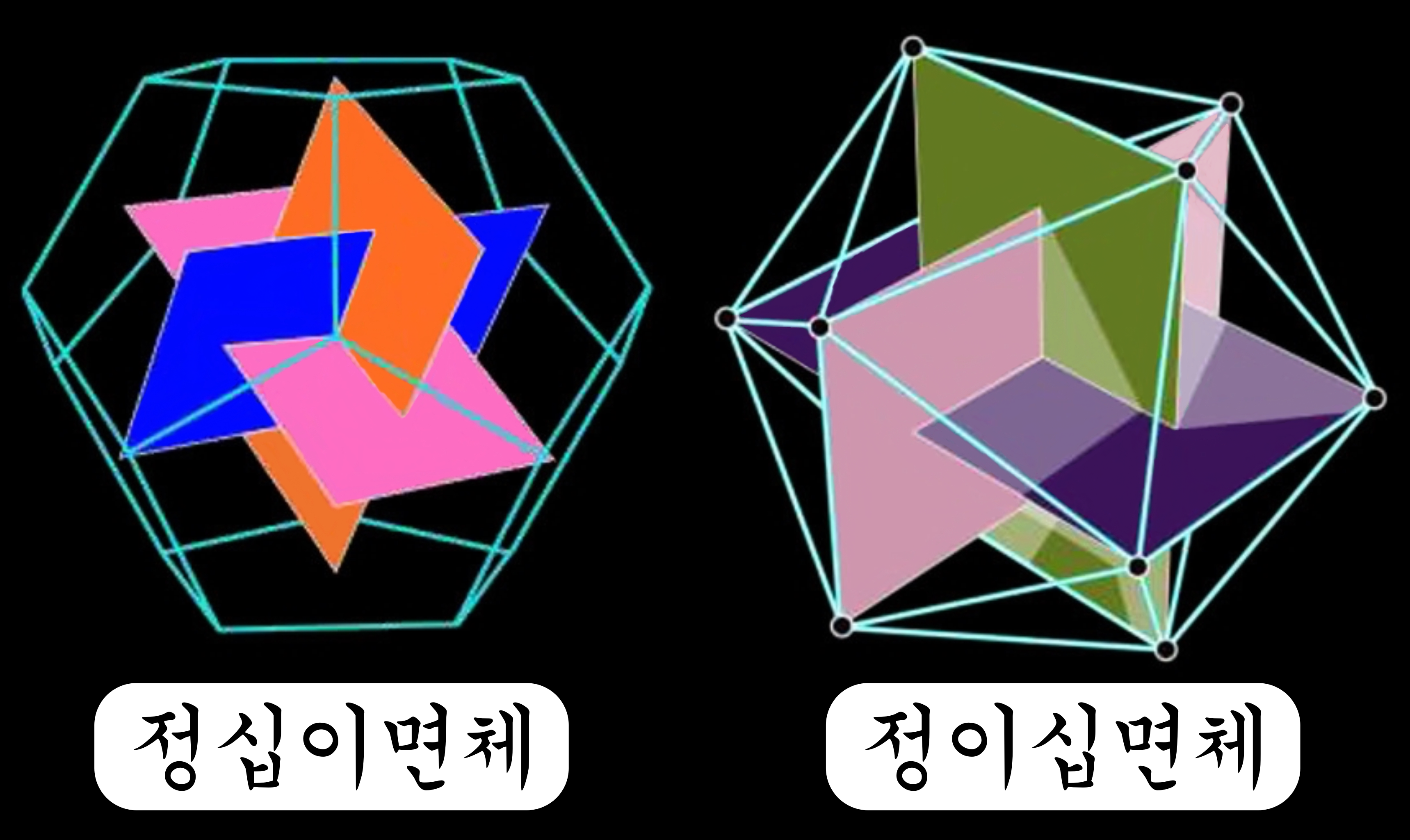
6. 지오데식 돔 (Geodesic Dome)
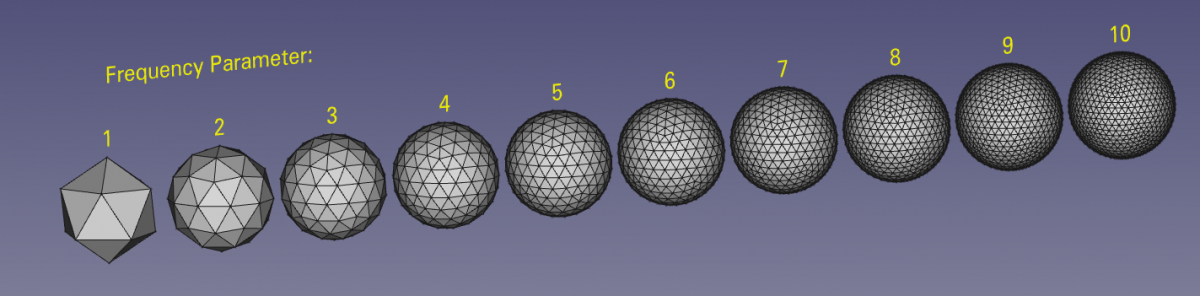
삼각형은 밖에서 가해지는 힘을 잘 견디는 구조이다. 변형에 강한 삼각형을 조합시킨 '트러스 구조(Truss Structure)'는 '다리 기둥의 도리'나 '돔 지붕' 등에 많이 사용된다. 20개의 정삼각형으로 이루어진 정이십면체를 출발저으로 해서 '꼭짓점과 변의 수'를 계속 늘려가면 구형에 가까운 돔 구조를 만들 수 있다. 그것이 '지오데식 돔(Geodesic Dome)'이다. '지오데식(Geodesic)'이란 '측지선(Geodesic Line, 구면 위에 있는 2점 사이의 최단 경로)'을 말한다. 가능한 측지선을 따라 골조를 만드는 돔이라고 해서 지오데식 돔이라는 이름이 붙었다. 고안자는 미국의 건축가 '리처드 버크민스터 풀러(Richard Buckminster Fuller, 1895~1983)'이다.
아래의 그림은 '리처드 버크민스터 풀러(Richard Buckminster Fuller)'가 고안한 '지오데식 돔'을 만드는 방법이다. 정십이면체를 구성하는 정삼각형을 더 작은 삼각형으로 분할한다. 4분할, 9분할, 16분할, 25분할... 이런식으로 더 많은 작은 삼각형으로 분할할수록 전체 모양이 '구(Sphere)'에 가까워진다. 이러한 분할 방법을 '지오데식 분할(Geodesic Division)'이라고 하며, '지오데식 분할'의 방법에는 여러 가지가 있다. 그런데 삼각형을 분할하면 정삼각형이 아닌 삼각형이 생기고, 꼭짓점에 따라 접하는 면의 수도 달라진다. 그래서 지오데식 돔은 정다면체가 아니다.
6-1. 몬트리올 바이오스피어
아래의 사진은 캐나다 '몬트리올(Montreal)'에 있는, 환경을 테마로 한 박물관 '몬트리올 바이오스피어(Montreal Biosphere)'이다. 돔의 지름은 76m이며, 지오데식 돔의 고안자인 '리처드 버크민스터 풀러(Richard Buckminster Fuller)'가 설계했다.

7. 아르키메데스 입체
'플라톤 입체'의 친척이라고 할 수 있는 '아르키메데스 입체(Archimedes Solid)'도 있다. 그 이름은 이 입체를 처음 열거한 고대 그리스의 수학자 '아르키메데스(Archimedes, 기원전 287?~21)'에서 유래했다. '아르키메스 입체'는 '반 정다면체(Semiregular Polyhedron)'라고도 불리는데 2종류 이상의 정다각형으로 에워싸이고 모든 변의 길이와 모든 꼭짓점에 모이는 각의 합이 같은 입체를 말한다. '아르키메데스 입체'는 전부 13종류가 있다.
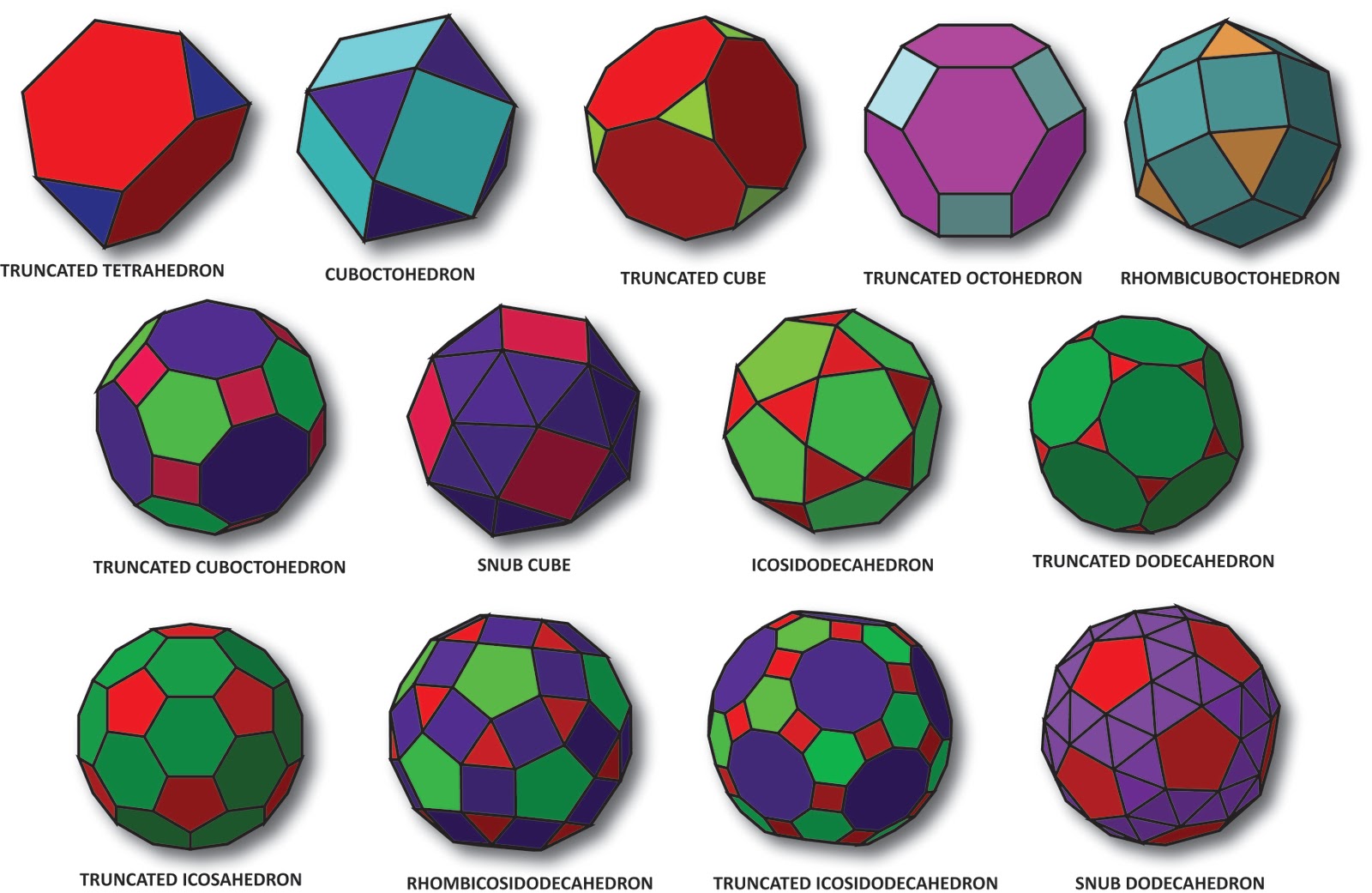
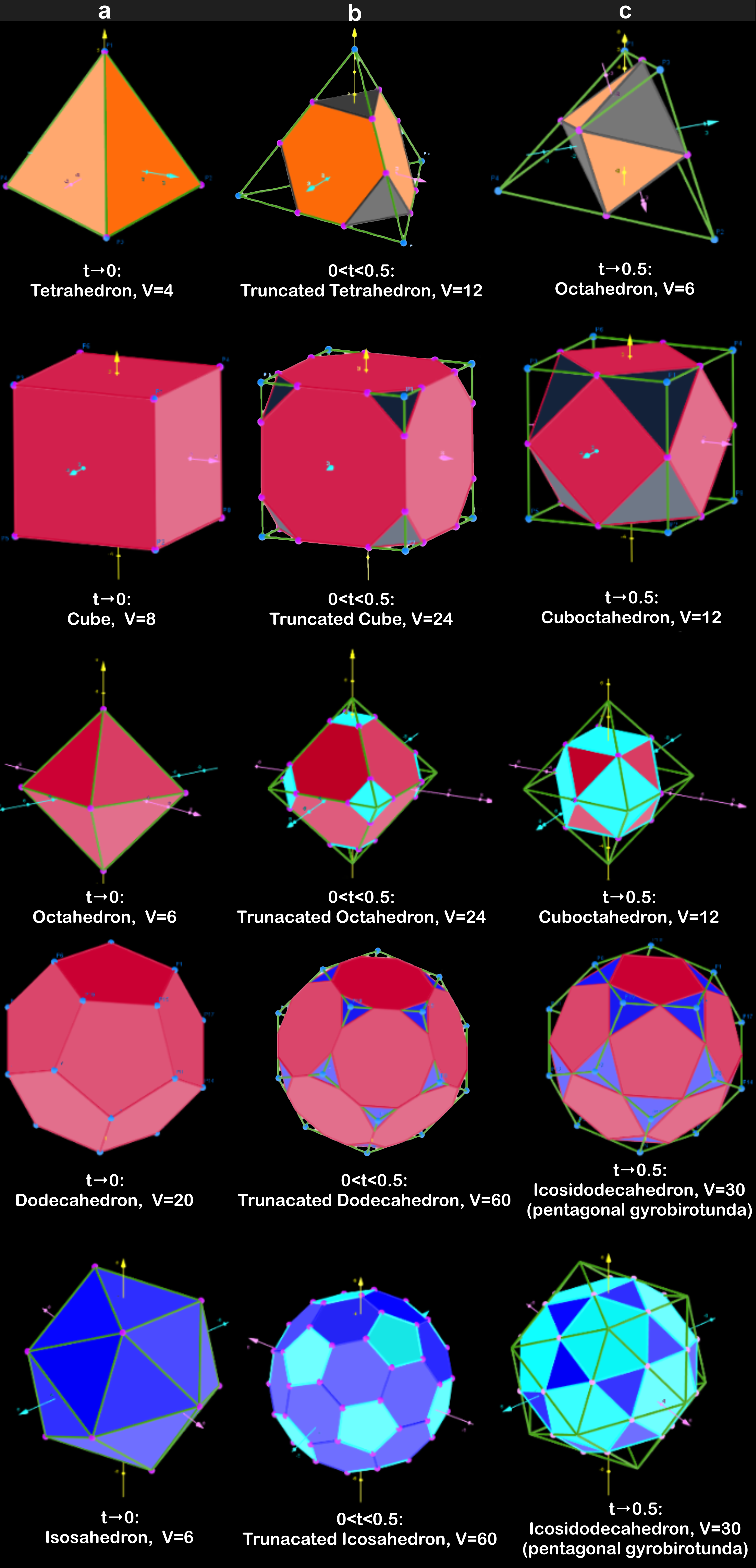
7-1. 플라톤 입체를 깎아서 아르키메데스 입체 만들기
'플라톤 입체'의 꼭짓점을 모든 변의 길이가 같아질 때까지 자르면, '깎은 정사면체(Truncated Tetrahedron)', '깎은 정육면체(Truncated Cube)', '깎은 정팔면체(Truncated Octohedron)', '깎은 정십이면체(Truncated Dodecahedron)', '깎은 정이십면체(Trauncated Icosahedron)'라는 5종류의 아르키메데스 입체를 만들 수 있다. 아르키메데스 입체를 이해하기 위해, 예컨대 정다면체의 하나인 정사면체의 꼭짓점을 중심을 향해 조금씩 잘라 나간다고 생각해 보자. 어느 부분까지 자르면 모든 변의 길이가 같아진다. 이것이 '아르키메데스 입체'의 하나인 '깎은 정사면체'이다.
'깎은 정이십면체(Truncated Octhohedron)'는 정이십면체의 꼭짓점을 잘라서 생기는 아르키메데스 입체이다. 깎은 정이십면체를 부풀려 둥글게 하면 축구공이 된다. 또 60개의 탄소 원자로 이루어지며 '깎은 정이십면체'의 구조를 가진 분자를 '버크민스터 풀러렌(Buckminster Fullerene)'이라고 한다. '버크민스터 풀러렌'은 의약품이나 반도체 재료 등으로 응용이 기대되는 분자이다. '지오데식 돔'과 비슷한 형태이기 때문에, 그 고안자인 '리처드 버크민스터 풀러(Richard Buckminster Fuller)'의 이름을 따서 명명되었다.
또 위에서 소개한 '쌍대(Dual)'와 '아르키메데스 입체'는 깊은 관계가 있다. 정이십면체의 꼭짓점을 자르면 깎은 정이십면체가 되지만, 이어 원래의 정이십면체 면의 중심까지 계속 자르면, 정이십면체와 쌍대 관계에 있는 정다면체인 '정십이면체'가 된다. 그 상태에서 계속 더 자르면 이번에는 깎은 정십이면체가 되었다가 마침내 원래의 정이십면체로 돌아간다.
8. 공간을 꽉 채우는 방법
'사면체 타일의 정리'에서 정사면체의 전개도로 평면을 가득 채울 수 있음을 설명했다. 그렇다면 2차원 도형이 아니라 3차원 입체로 공간을 빈틈없이 채울 수는 없을까? '플라톤 입체' 또는 '아르키메데스 입체'만을 사용해 공간을 빈틈없이 꽉 채우는 방법은 아래에 제시한 3가지뿐이다.
- 정육면체: 공간을 꽉 채울 수 있는 가장 알기 쉬운 입체는 정육면체이다. 정육면체는 일반적으로 단순하게 쌓으면 틈새 없이 공간을 꽉 채울 수 있다.
- 깎은 정팔면체: '플라톤 입체' 중에서 정육면체 이외에 정사면체와 정팔면체를 조합시킴으로써 공간을 꽉 채울 수 있다. '아르키메데스 입체' 중에는 '깎은 정팔면체'만 단독으로 공간을 꽉 채울 수 있다.
- 정사면체와 정팔면체: 가장 단순한 정다각형인 정삼각형은 평면을 꽉 채울 수 있다. 하지만 입체가 되면 가장 단순한 정다면체인 정사면체는 단독으로 공간을 꽉 채울 수 없다. 차원이 바뀌면 가득 채우기 위해 필요한 조건도 바뀌는 것이다. 단, 정사면체와 정팔면체는 각각 단독으로는 공간을 꽉 채울 수 없지만, 둘을 조합시킴으로써 틈새 없이 쌓아 올릴 수 있다.
'정사면체'와 '깎은 정사면체', '정팔면체와 깎은 정육면체' 등 '플라톤 입체'와 '아르키메데스 입체'를 조합해 공간을 꽉 채우는 방법도 있다. 또 '플라톤 입체'와 '아르키메데스 입체'에 한정하지 않으면, 공간을 꽉 채울 수 있는 입체는 수없이 많이 존재한다. 예컨대 '삼각기둥'이나 '육각기둥' 등으로 공간을 꽉 채우는 일이 가능하다.
