0. 목차
- '난수'란 무엇인가?
- 몬테 카를로법(Monte Carlo Method)
- 클러스터 착각(Cluster illusion)
- 정규수(Normal Number)
- 의사 난수 발생법
- 물리 난수 발생법
- 난수가 우리 사회를 지탱하고 있다.

1. '난수'란 무엇인가?
'난수(Random Number)'란 '다음 수를 결정하는 법칙이 절대 존재하지 않는 수'를 말한다. 다른 말로 하면, '다음에 무엇이 나올지 전혀 알 수 없는 수'가 난수이다. 그리고 난수를 만들어내는 장치를 '난수 발생기(Random Number Generator)'라고 한다. 예컨대 정육면체 주사위는 1에서 6까지의 난수를 만드는 난수 발생기이다.
정이십면체의 각 면에 0부터 9까지의 숫자를 2번씩 할당하면, 0부터 9까지의 난수를 만드는 난수 발생기가 된다. 이것을 '난수 주사위'라고 하며, 이것을 계속 굴려 수학책에 실린 것과 같은 '난수표(Table of Random Numbers)'를 만들 수 있다. 색으로 구분한 3개의 난수 주사위를 준비하고, 예를 들어 빨간색 숫자를 소수 첫째 자리, 노란색 숫자를 소수 둘째 자리, 파란색 숫자를 소수 셋째 자리라고 하면, 0.000에서부터 0.999까지의 3자리 난수가 생긴다.
만약 주사위의 눈이 무작위가 아니라, 다음에 나올 눈을 미리 예측할 수 있다면 주사위 게임은 시시해진다. 빙고 게임이나 경품 추첨에 사용하는 '번호 추출기'나 도박장의 룰렛 등도 일종의 난수 발생기이다. 컴퓨터 게임에서도 상대 캐릭터의 움직임이 단조롭지 않도록 난수가 사용된다. 컴퓨터 게임에서도 상대 캐릭터의 움직임이 단조롭지 않도록 난수가 사용된다. 컴퓨터 게임에서도 상대 캐릭터의 움직임이 단조롭지 않도록 난수가 사용된다.
2. 몬테 카를로법(Monte Carlo Method)
난수가 활용되는 것은 게임만이 아니다. '과학 연구'나 '인공지능(AI)'의 개발에도 난수가 사용된다. 그 중요한 예가 난수를 사용해 수치 계산이나 시뮬레이션을 하는 '몬테 카를로법(Monte Carlo Method)'이다. 바둑 기사 '이세돌'을 이긴 '알파고(AlphaGo)'도 '몬테 카를로법'을 사용해 방대한 수의 대국을 경험·학습하면서 강해졌다.
2-1. '몬테 카를로법'으로 원주율 π의 값 구하기
한 예로, 여기에서는 '몬테 카를로법(Monte Carlo Method)'을 사용해 원주율 π의 값을 구할 수 있는 방법을 소개한다. 정이십면체 주사위를 준비해서 스스로 원주율을 구해보자. 이것은 '몬테 카를로법'을 가장 단순하게 응용한 예이다.
- 1단계: 정이십면체의 난수 주사위를 3개를 굴려 3자리 난수를 2개 만든다. 예컨대 0.294과 0.479가 나왔다고 하자.
- 2단계: 2개의 난수를 xy 좌표로 하는 점을 만든다. (x, y)=(0.294, 0.479)가 될 것이다.
- 3단계: 이것을 몇 차례 반복하여 다수의 점을 만든다.
- 4단계: 다수의 점을 한 변의 길이가 1인 정사각형 위에 찍는다. 이 정사각형 위에 반지름이 1인 부채꼴을 그린다. 정사각형의 넓이는 1이고, 반지름이 1인 원의 넓이는 반지름×반지름×π이므로, 그 4분의 1인 부채꼴의 넓이는 π/4이다. 결국 정사각형에서 차지하는 부채꼴 넓이의 비율은 π/4인 셈이다. 이런 식으로 점을 찍는 횟수를 늘려나가면. π=3.141592...에 수렴한다.

3. 클러스터 착각(Cluster illusion)
주사위를 던져 다섯 차례 연속으로 6이 나왔다. 이것을 보고 '1이 나오기 쉽게 조작한 것이 아닐까?' 의심하는 사람이 있을 수 있다. 심리학 연구에 따르면, 실제로는 우연인데도 이따금 같은 사건이 계속해 일어나면, 그것을 우연히 아니라고 착각하는 경향이 있다. 이것을 '클러스터 착각'이라고 한다.
'클러스터 착각(Cluster illusion)'의 예로는, 제2차 세계 대전 말기의 영국 런던을 공격한 독일군의 미사일이 유명하다. 미사일이 떨어지는 빈도가 지역별로 달랐기 때문에, 런던 시민의 일부는 '독일군의 미사일은 특정 지역을 노린다'면서 두려워했다. 그러나 나중에 분석한 결과, 미사일의 탄착점은 무작위였음이 밝혀졌다. 사람은 우연한 사건이 중복되면 의미가 있을 것 같은 패턴을 찾으려는 경향이 있다.
또 하나의 클러스터 착각의 예를 소개한다. 미국의 유명 고생물학자이며 진화 생물학자인 '스티븐 제이 굴드(Stephen Jay Gould, 1941~2002)'는 저서 'BULLY FOR BRONTOSAURUS - Reflection in Natural History(1995)'에서 다음과 같은 이야기를 소개했다. '아래 2개의 그림 가운데, 점이 무작위로 분포한 것은 어느 쪽일까?'라고 묻자 많은 사람이 '왼쪽이 무작위'라고 대답했다. 그러나 실제로는 왼쪽은 점이 겹치지 않도록 의도적으로 배치한 것이고, 오른쪽은 무작위로 분포한 것이다. 왼쪽 그림에서는 의미가 있을 것 같은 패턴이 읽히지 않기 때문에 '더 무작위하다.'고 판단하기 쉽다.
이런 착각은 심리학에서 자주 연구되며, 인간의 심리 경향으로 경제 현상을 설명하는 '행동 경제학'이라는 분야에서 응용되고 있다. 인간의 직감이 빠지기 쉬운 착각을 역으로 이용하면, '더 자연스러운 우연성'을 연출할 수 있다. 디지털 음악 플레이어나 음악 스트리밍 서비스의 '셔플 재생(무작위 선곡)'에는 특정 아티스트의 곡이 계속 선곡되지 않게 하는 등, 의도적으로 우연성을 줄여 '보다 자연스러운 우연'을 느낄 수 있게 고안된 것이 있다. 같은 방식이 컴퓨터 게임에도 응용되고 있다.

4. 정규수(Normal Number)
당신이 게임 프로그래머라고 가정하자. 게임에 나오는 'NPC(Non-Player Character)'의 움직임을 플레이어가 예측하지 못하도록 하기 위해 난수를 사용해 움직임을 정하기로 했다. 0부터 9까지의 난수를 컴퓨터가 만들어내는 손쉬운 방법으로, 당신은 '원주율(π)'을 사용하기로 생각했다. '원주율(π=3.141592)'을 계산으로 구하면, 소수점 이하의 숫자가 무한히 이어진다. 이들 숫자 열에는 어떠한 규칙성도 발견되지 않는다. 하지만 원주율이 나타내는 숫자 열을 과연 과연 난수라고 할 수 있을까?
'1이 나오기 쉬운 주사위'는 난수를 만들기에 적합하지 않다. 이와 마찬가지로, 난수에서는 각각의 숫자가 같은 빈도로 나와야 한다. 그렇다면 원주율의 숫자는 어떨까? 아래의 그래프는 원주율의 소tn점 이하 5만 자리까지에 대해 0부터 9까지의 숫자의 출현 빈도를 조사한 것이다. 가장 많은 것은 '8'이고 가장 적은 것은 '6'이었다. 그러나 그 차이는 극히 적어서, 0부터 9까지의 숫자가 나오는 빈도는 거의 같다고 간주할 수 있다. 그러면 '원주율(π)'이나 '2의 제곱근'에 나열된 숫자는 어디까지 가도 0부터 9까지의 숫자가 나타나는 빈도에 편향이 없다고 단정할 수 있을까?
소수로 표시했을 때의 숫자 열에 0부터 9까지의 숫자에 편향이 전혀 없는 수를 가리켜 수학에서는 '정규수(Normal Number)'라고 한다. 하지만 '원주율(3.141592...)'이나 '2의 제곱근(1.414213...)'이 정규수인지 아닌지는 아직 까지도 모른다. '원주율(π)'이나 '2의 제곱근'에서 나열된 수가 진정한 난수인지는 해결되지 않은 수수께끼라고 할 수 있다.
5. 의사 난수 발생법
'게임'이나 '몬테 카를로법'의 프로그램을 구동시키기 위해 컴퓨터는 많은 난수를 필요로 한다. 그런데 컴퓨터는 스스로 난수를 만들어낼 수 있을까? 컴퓨터가 수의 열을 만들기 위해서는 프로그램이나 알고리즘 등의 규칙이 필요하다. '다음 수를 정하는 규칙이 전혀 존재하지 않는 수'가 난수이기 때문에 컴퓨터가 규칙에 따라 만드는 수의 열은 진정한 의미에서는 난수라고 할 수 없다. 그래서 진정한 난수를 대신하는 것이 마치 난수처럼 보이는 '의사 난수(Rseudo Random)'이다.
'의사 난수'를 처음으로 고안한 사람은 컴퓨터 발명자로 널리 알려진 헝가리 출신의 미국 수학자 '존 폰 노이만(John Von Neumann, 1903~1957)'이다. '폰 노이만'이 고안한 '재제곱 채중법'이 의사 난수의 원조이다. '의사 난수'를 만드는 알고리즘에는 '재제곱 채중법(Midsquare Method)' 외에 '선형 합동법(Linear Congrential Generator)', '메르센 트위스터법(Mersenne Twister Method)'도 있다.
5-1. 재제곱 채중법 (4자리의 경우)
'재제곱 채중법(Midsquare Method)'을 이용해 4자리의 '의사 난수'를 만들어보자. 우선 시각표 등에서 '난수의 종자'가 될 4자리의 수를 택한다. 여기에서는 '난수의 종자'가 될 4자리의 수를 '씨앗'이라고 하자. '씨앗'을 제곱한 8자리의 수 가운데 4자리의 수를 첫 번째 의사 난수로 삼는다. 제곱해도 자릿수가 채워지지 않을 때는 0을 보충한다. 이 5227을 같은 방법으로 조작해 다음의 의사 난수 3215를 얻는다. 이것을 반복하며 차례차례 의사 난수를 만드는 것이 '재제곱 체중법(Midsquare Method)'이다.

5-2. 선형 합동법 (4자리의 경우)
'선형 합동법(Linear Congrential Generator)'을 이용해 4자리의 '의사 난수'를 만들어보자. '씨앗이 되는 수(여기서는 1234)'에 '미리 정해둔 상수(여기서는 567)'를 곱하고, '거기에 다른 상수(여기에서는 89)'를 더한다. 이 수를 '또 다른 상수(여기서는 9973)'로 나누었을 때의 나머지를 구한다. '이 나머지(여기서는 1657)'를 첫 번째 의사 난수로 한다. 이 1657에 같은 조작을 해서 두 번째 의사 난수 2146을 얻는다. 이 2146에 같은 조작을 해서 세 번째 난수 165를 얻는다. 이 165에 같은 조작을 해서 네 번째 난수 3887을 얻는다. 이 과정을 반복하며 차례차례 의사 난수를 만드는 방법이 '선형 합동법'이다. 덧셈에 사용하는 상수를 0으로 하는 경우도 있다.
- 1234 × 567 + 89 = 699767 → 699767을 9973으로 나눈 나머지 = 1657
- 1657 × 567 + 89 = 939608 → 939608을 9973으로 나눈 나머지 = 2146
- 2146 × 567 + 89 = 1216871 → 1216871을 9973으로 나눈 나머지 = 165
- 165 × 567 + 89 = 93644 → 93644을 9973으로 나눈 나머지 = 3887
- 이 과정을 반복한다.
5-3. 메르센 트위스터법
'존 폰 노이만(John Von Neumann)' 이후 다양한 의사 난수가 개발되었다. 의사 난수의 좋고 나쁨은 '진정한 난수와 비슷한 정도'와 '의사 난수의 발생 속도' 등으로 결정된다. 현시점에서 가장 좋은 의사 난수로 평가되며, 전 세계 프로그래머들이 널리 사용하는 방법은 '메르센 트위스터법(Mersenne Twister Method)'이다. '메르센 트위스터법'은 일본 히로시마 대학의 '마쓰모토 마코토' 교수와 야마가타 대학의 '니시무라 다쿠지' 부교수 등이 1998년에 고안하였다.
이것을 이해하는 데는 '벡터(Vector)'와 '행렬(Matrix)'이라는 수학 지식이 필요하기 때문에 여기서는 자세한 설명을 생략한다. 다만 '메르센 소수'라는 특수한 소수의 성질이 이용된다는 것만 알아두자. 현시점에서 가장 좋은 의사 난수 생성법인 '메르센 트위스터법'도 어디까지나 '의사 난수(Pseudo Random)'이지 '진정한 난수'는 아니다. '의사 난수'의 아버지인 '폰 노이만'도 '수식으로 난수를 만드는 것은 일종의 죄'라는 말을 했다.
6. 물리 난수 발생법
컴퓨터가 만들어낸 '의사 난수'는 실용적인 측면에서는 충분히 유용하지만, 엄밀한 의미에서는 진정한 난수라고 할 수는 없다. 그러면 '진정한 난수(어떤 규칙성도 발견할 수 없는 난수)'를 만들려면 어떻게 해야 할까? 그 방법은 현실 세계의 물리 현상에서 나타나는 불규칙성을 이용해 난수를 만드는 것이다. 이 방법을 '물리 난수 발생법'이라고 한다.
6-1. 전기 회로에서 나타나는 노이즈를 이용하는 방식
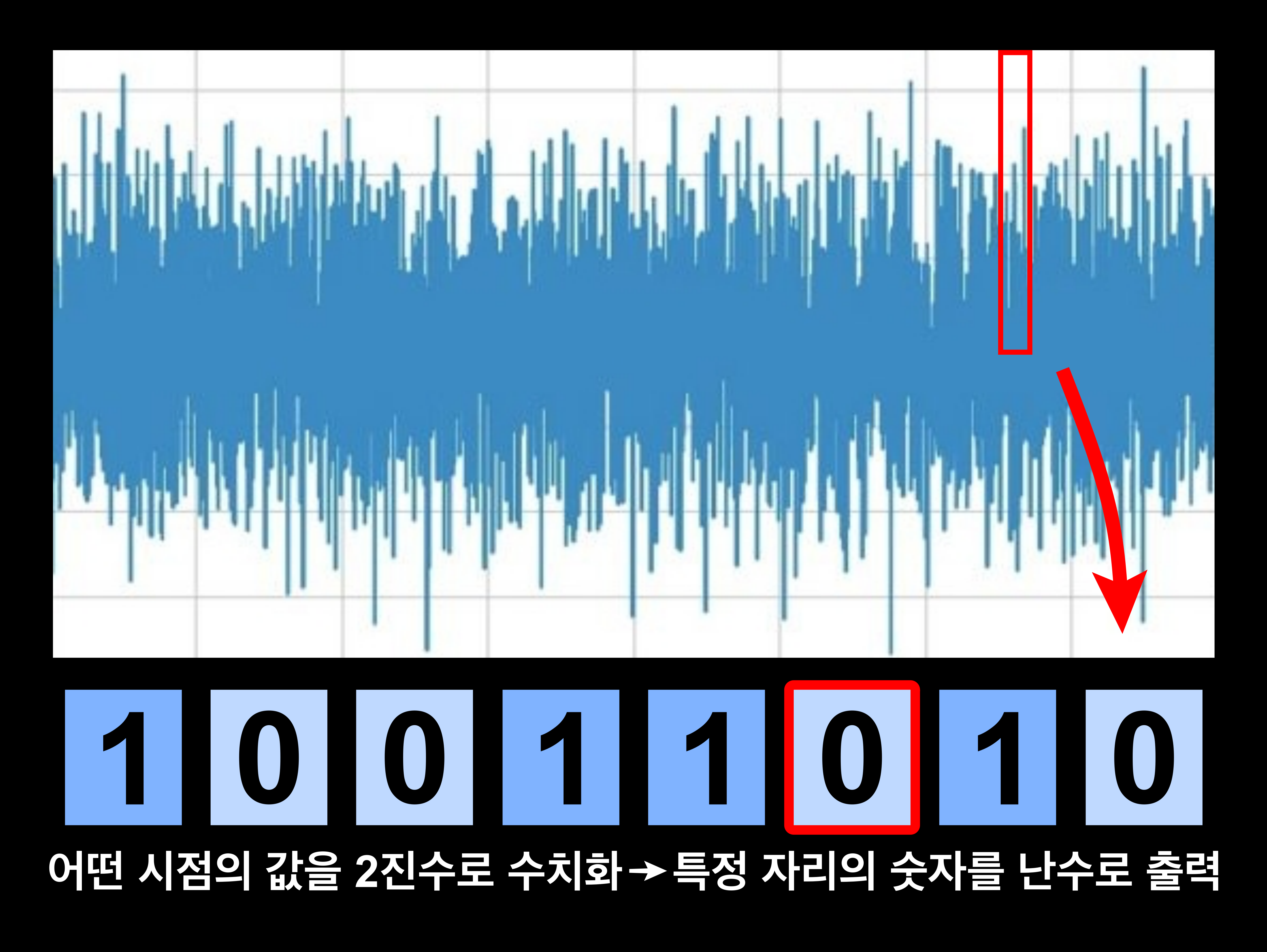
가장 실용화된 '물리 난수 발생법'은 전기 회로에서 나타나는 전압 노이즈를 이용하는 방식이다. 전기 회로에 걸린 전압을 아무리 일정하게 유지하려고 해도, '열잡음'이라는 미세한 노이즈가 생겨난다. 이 노이즈에는 어떤 규칙성도 없기 때문에, 이것을 수치로 추출하면 난수로 활용할 수 있다. 일정 시간별로 전압을 측정해 수치화하고, 그것을 2진수의 수로 나타낸다. 그 일부 자릿수를 추출하면 0과 1로 이루어진 2진수의 난수가 된다. 일부 고성능 컴퓨터에는 '열잡은 방식'의 물리 난수 발생칩이 탑재되어 있다.
6-2. 빛이나 전자를 동전 대신 사용하는 방법
'물리 난수 발생법'에는 빛의 소립자인 '광자(Photon)'를 사용하는 방식도 있다. 어떤 특수한 '반투명 거울(Half Mirror)'에 부딪친 1개의 광자는 '편광(진동 방향의 편향)'이라는 성질에 따라 50% 확률로 투과하고 50% 확률로 반사한다. 동전의 양면처럼 광자가 투과하면 0, 반사하면 1이라고 하면 2진수의 난수가 된다.
더 나아가 전자가 가진 '스핀(Spin)'이라는 성질을 이용하는 방식도 연구된다. 지구에 '자전축(Rotation Axis)'이 있듯이, 전자 등의 소립자에서 자전축에 해당하는 것이 '스핀의 방향'이다. 양자 역학에 따르면 1개의 전자는 '스핀이 위 방향인 상태'와 '스핀이 아래 방향인 상태'가 겹쳐 있으며, 어느 상태인지는 관측할 때까지 알 수 없다. 전자를 관측해서 스핀이 위 방향이면 0, 아래 방향이면 1로 해서 2진수의 난수로 사용할 수 있다.
7. 우리 사회를 지탱하는 '난수'
'의사 난수'나 '물리 난수'는 컴퓨터 게임의 프로그램이나 '몬테카를로법'을 사용한 과학 연구의 시뮬레이션, AI 개발 등에서 빼놓을 수 없다. 그리고 PC, 인터넷, 스마트폰 등이 널리 보급된 오늘날의 사회에서 난수는 매우 중요한 역할을 담당하고 있다. '이메일(E-Mail)'이나 '카카오톡(Kakao Talk)' 등의 '어플리케이션(Application)', 온라인 쇼핑 등의 정보 통신에는 '암호화'라는 기술이 사용된다. 통신 내용을 암호화하거나 암호화된 문장을 해독하기 위한 '열쇠'를 만들 때, 그때마다 난수가 사용된다. 또 은행의 '온라인 뱅킹', '트위터(Twitter)'나 '페이스북(Facebook)' 등의 'SNS(Social Networking Service)'의 2단계 인증 등에는 한 번만 사용할 수 있는 '1회용 비밀번호(OTP: One Time Password)'가 사용된다. '1회용 비밀번호(OTP)'를 발행하는 메커니즘에도 '난수'가 사용된다.