0. 목차
- '차원'이란 무엇인가?
- 2차원
- 3차원
- 높은 차원은 그보다 낮은 차원의 공간을 내부에 포함한다.
- 차원의 확장
- 초입체
- 낮은 차원에서 불가능한 일도 높은 차원에서는 가능하다.
1. '차원'이란 무엇인가?
1-1. 유클리드가 정의한 점, 선, 면
'차원(dimension)'이란 공간이나 도형이 넓어지는 정도를 나타내는 개념이다. 차원의 개념은 기원전부터 있었던 것 같다. '기하학의 시조'라 불리는 고대 그리스의 수학자 '유클리드(Ευκλείδης, 기원전 330?~275)'는 기하학에서 그때까지 이루어진 성과를 체계화해 '원론'을 썼다. 그는 '원론'에서 점, 선, 면, 입체 등의 정의를 다음과 같이 내렸다. '점이란 부분을 갖지 않는 것이다. 선이란 폭이 없는 길이이다. 면이란 길이와 폭만 가진 것이다. 입체란 길이와 폭과 높이를 가진 것이다.' 유클리드의 '원론'의 본문에는 방금 언급한 정의 이외에 '선의 끝은 점, 면의 끝은 선, 입체의 끝은 면'이라는 정의도 적혀있다.
한편, 고대 그리스의 철학자인 '아리스토텔레스(기원전384~기원전 3222)'는 저서 '천체론'에서 다음과 같이 말했다. "입체는 완전하며, 3차원을 넘는 차원은 존재하지 않는다."

1-2. '데카르트'의 정의
'나는 생각한다. 고로 존재한다.'라는 말을 한것으로 유명한 철학자 '데카르트(René Descartes, 1596~1650)'는 '좌표(Coordinates)'의 개념을 확립한 수학자이기도 하다. '데카르트'에 의하면, '차원은 한점의 위치를 정하기 위해 필요한 수치의 개수'라고 정의할 수 있다.
- 0차원: 크기가 없는 '점' 안에서는 그 위치를 정할 수 없으므로 0차원이다. 0차원인 '점'은 위치 결정에 필요한 수치가 없다.
- 1차원: '직선(Straight Line)'에서는 거리에 해당하는 1개의 수(예컨대 x=2)를 주면 한 점의 위치가 정해진다. 반대 방향으로 나아갈 때는 거리에 음수를 붙인다. 직선뿐만 아니라 곡선에서도 그 원리는 같으므로 '곡선도 1차원'이다. 1차원인 '선'에서 위치 결정에 필요한 수치는 1개이다.
- 2차원: '면'은 2차원이다. 예컨대 모눈종이에서는 가로와 세로의 눈금을 지정하는 수치(예컨대 x=2, y=3)를 지정하면 한 점의 위치가 정해진다. '지구의 표면'도 위도와 경도라는 2개의 수치로 위치를 특정할 수 있으므로 2차원이다. 2차원인 '면'에서 위치 결정에 필요한 수치는 2개이다.
- 3차원(우리가 살고 있는 공간): 그러면 '우리가 살고 있는 공간'은 몇 차원일까? '우리가 살고 있는 공간'은 3차원이다. '우리가 살고 있는 공간'에서는 가로와 세로 높이의 수치(예컨대 x=5, y=3, z=6)'를 지정하면 한 점의 위치가 정해진다. 예컨대 항공기의 위치를 특정할 경우, 위도와 경도라는 2차원 정보에 덧붙여 높이라는 정보가 필요하다. 즉, 항공기의 위치는 위도, 경도, 높이라는 3개의 수치를 사용해 위치를 파악한다. 실제로 항공기에 탑재된 'GPS(위성 위치 확인 시스템)'는 이 3개의 수치로 현재의 위치로 파악한다. 자동차 내비게이션의 경우, 위도와 경도 그리고 해발 고도의 수치로 위치를 특정한다. 3차원인 '공간'에서 위치 결정에 필요한 수치는 3개이다.
2. 2차원
1차원의 '직선'의 경우, 직선 위에 있는 두 영역 A, B가 있을 때 이 둘을 비교하는 척도는 길이뿐이다. 2차원의 '면'의 경우, 면 위에 있는 두 영역 A, B는 넓이로 비교할 수 있다. 하지만 2차원에서는 넓이 이외의 특징에 의해서도 비교할 수 있다. 그 특징이란 바로 '형태'이다. 2차원 세계에서는 삼각형이나, 원, 타원 또는 곡선으로 둘러싸인 불규칙한 도형 등, 1차원에는 없는 다양한 '형태'가 등장한다. 형태를 다루는 수학인 '기하학'은 1차원에는 없고, 2차원이 되어서야 비로소 등장한다. '각도'나 '회전'이라는 말도 2차원의 세계에 와서야 의미를 지닌다.
그러면, 이쯤에서 의문스럽게 생각하는 사람들이 있을지도 모르겠다. 1차원에서 곡선의 '구부러지는 정도'는 2차원의 '형태'에 해당하는 것은 아닐까? 이런 의문에 대한 답은 우리가 3차원 공간에서 바라보고 있기 때문에 나오는 의문이다. 1차원에 사는 생물이 있다면, 그들에게 방향은 '앞뒤'밖에 존재하지 않을 것이다. 1차원 생물은 선을 따라서만 나아갈 수 있으며, 앞뒤를 보아도 '점'밖에 보이지 않을 것이다. 2차원 또는 3차원 세계에서 선이 구부러져 있다고 해도, 1차원 생물은 그것을 볼 수 없다.
- 직소 퍼즐: '직소퍼즐'은 2차원이다. 그러면 1차원의 '직소 퍼즐(하나의 그림을 여러 개의 조각들로 나누어 뒤섞은 뒤, 그것을 하나의 그림으로 다시 조립하는 놀이)'은 어떻게 될까? 1차원의 직소 퍼즐은 한 가닥의 선을 여러 길이로 자르고 그것을 뒤섞은 다음, 다시 한 가닥의 형태로 연결하는 퍼즐이 될 것이다. 하지만 이 퍼즐은 아무런 재미도 없다. 잘린 각 조각의 양 끝은 모두 점이기 때문에, 어느 조각이든지 서로 연결할 수 있다. 직소 퍼즐이 재미있는 이유는 그것이 2차원이기 때문이다. 2차원이 가지고 있는 '형태'에 주목해, 어느 조각과 어느 조각이 서로 연결되는지 시행착오를 겪어야 하기 때문에 재미있는 것이다.
- QR코드: 2차원은 1차원에 비해 복잡한 성질을 가지고 있다. 즉, 2차원은 1차원보다 많은 정보를 가지고 있다. 그래서 근년에는 이러한 성질을 이용한 '2차원 바코드(QR코드)'가 보급되었다. 1차원 바코드는 가로 방향으로만 정보를 가지고 있지만 2차원 바코드는 세로 방향으로도 정보를 가질 수 있다. 그래서 '2차원 바코드(QR코드)'는 1차원 바코드보다 수십~수백 배의 정보량을 담을 수 있다.


3. 3차원
위에서 2차원의 세계, 즉 '면' 위에서는 삼각형이나 사각형, 원 등의 넓이를 가진 다양한 도형이 존재할 수 있음을 이야기했다. 한편 3차원에서는 '부피(volume)'를 가진 '입체(solid)'가 등장할 수 있다. 입체는 평면 도형보다 훨씬 복잡하다.
평면 도형에 다양한 형태가 있는 것처럼, 입체에도 '육면체(Hexahedron)', 구(Sphere), 원뿔(Circular cone), 정사면세(Tetrahedron) 등 다양한 형태가 있다. 그리고 입체에서는 2차원에서 허용되지 않고 3차원에서만 허용되는 특징 중에는 '뚫린 구멍을 가질 수 있다.'라는 것이다. 예를 들면, '도넛'이나 '손잡이가 뚫린 찻잔'은 뚫린 구멍을 가지고 있다. 하지만 2차원에서는 뚫린 구멍을 가진 도형은 존재하지 않는다. 예컨대 정사각형 윗변에서 구멍을 파면 '요(凹)'자가 되며, 그 구멍을 아랫변 쪽으로 연장해서 관통시키면, 2개의 직사각형으로 나누어져 버린다.
3차원이 가지고 있는 '뚫린 구멍을 가질 수 있다'라는 성질은 사실 인간에게 매우 중요하다. 사실 인간도 '뚫린 구멍'을 가지고 있는 입체이기 때문이다. 인간에게 있는 뚫린 구멍이란 '입'에서 '항문'으로 이어지는 소화관을 말한다. 몸을 관통하는 소화관은 3차원에서는 허용되지만, 2차원에서는 허용될 수 없다. 왜냐면, 2차원에서 몸을 관통하도록 구멍을 뚫으면, 그것에 의해 몸이 둘로 갈라져 버리기 때문이다.

3-1. 은하 좌표
좌표를 설정하여, 태양계나 우리 은하'의 규모에서도 위치를 3개의 수치로 나타낼 수 있다. 예컨대 '우리은하'안의 천체의 위치를 나타내려면, 우리 은하의 중심 방향과 은하면을 기준으로 한 은하 좌표(은위, 은경), 및 지구로부터의 거리라는 3개의 수치로 파악할 수 있다. 따라서 우리가 살고 있는 공간은 3차원이라고 말할 수 있다.
- 은위: 은하 좌표에서의 위도. 은하 적도에서 남북으로 각각 0°에서 90°까지 있다.
- 은경: 은하 좌표에서의 경도. 은하면의 북극에서 보아 은하의 중심 방향에서 시계 반대 방향으로 측정하며, 0~360°까지 있다.
4. 높은 차원은 그보다 낮은 차원의 공간을 내부에 포함한다.
4-1. 그림자는 도형이 가진 정보의 일부일 뿐
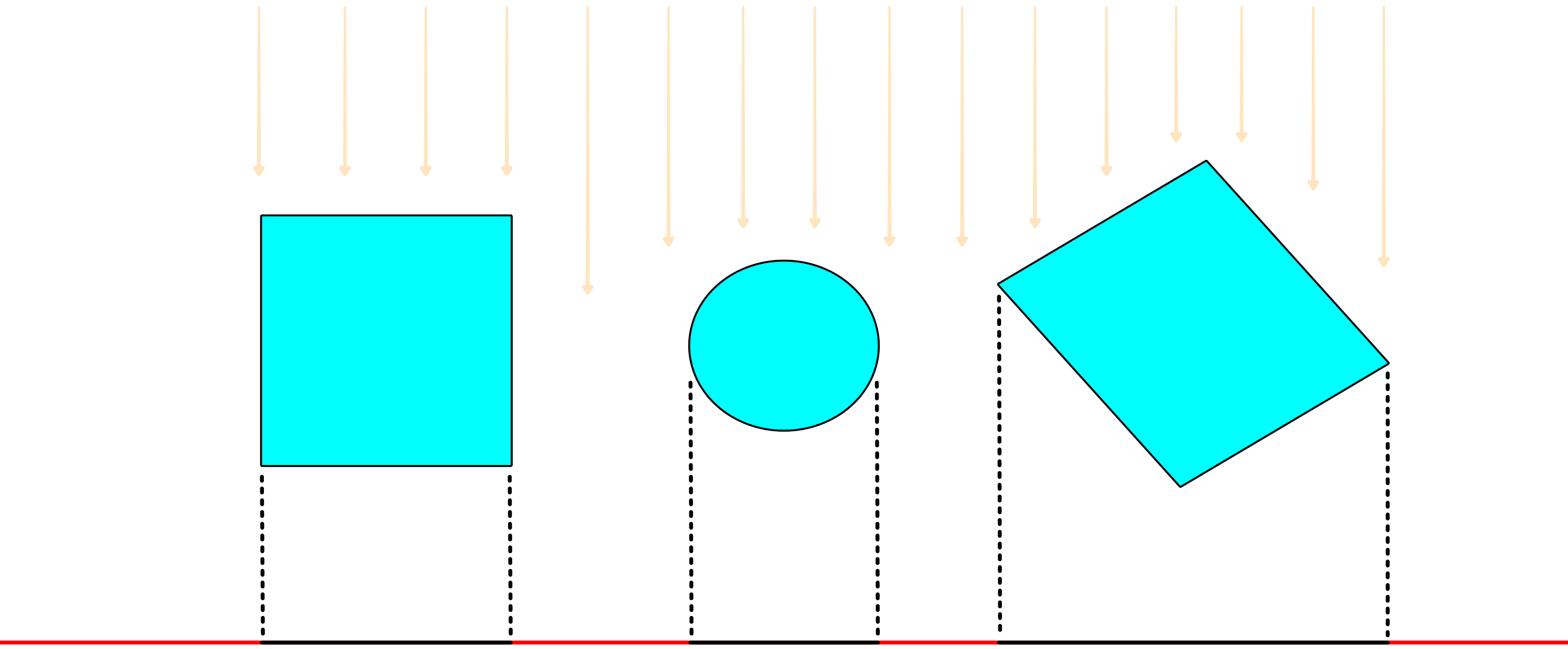
3차원의 공간에는 입체뿐만 아니라 2차원의 면, 1차원의 선, 0차원의 점도 존재할 수 있다. 마찬가지로 2차원 평면에는 선과 점이 존재할 수 있다. 즉, 높은 차원은 그보다 낮은 차원의 공간을 내부에 포함한다. 예컨대 3차원과 2차원 사이에는 '입체'와 '그림자'의 관계라는 중요한 관계가 있다. 3차원의 입체에 빛을 비추면, 2차원의 면 위에 그림자가 생긴다. 그리고 그림자의 모양은 원래의 입체의 형태에 따라, 빛을 비추는 방향에 따라, 광원과 입체 사이의 위치 관계에 따라서 그림자의 형태는 달라진다. 예컨대 구에 빛을 비추면 그림자는 원이나 타원이 되고, 직육면체에 빛을 비추면 그림자는 직사각형이나 육각형 등이 된다.
입체와 그림자의 관계에 대해서 몇 가지의 경우를 생각해 보자. 그림자가 원인 경우, 그 그림자의 바탕이 되는 입체는 '구(Sphere)'일까? 반드시 그렇지는 않다. 그림자가 원이 되는 입체는 '구'일 수도 있지만 '원기둥'이나 '원뿔'일 수도 있다. 그러면 정육면체가 드리우는 그림자는 어떤 모양일까? 정육면체의 그림자는 '정사각형'일수도 있지만 직사각형이나 육각형이 될 수도 있다. 또 입체 도형 중에는 어떤 방향에서 비추면 그림자가 원이 되고, 다른 방향에서 비추면 그림자가 삼각형이 되고, 또 다른 방향에서 비추면 그림자가 정사각형이 되는 것도 있다. 이처럼 평면에 드리우는 그림자는 원래의 입체를 어느 방향에서 바라본 '형태'의 정보에 지나지 않는다.
이처럼 높은 차원의 입체나 도형이 낮은 차원에 드리우는 그림자는 원래의 입체나 도형의 일부 정보밖에 가지고 있지 않다. 그래서 차원의 이러한 성질은 '4차원의 공간'을 생각할 때 힌트가 되기도 한다.
4-2. 사영
물체의 그림자를 만드는 것을 '사영'이라고 한다. '사영(Projection)'이란 물체가 가진 정보 가운데 더 낮은 차원에 속하는 일부의 정보만을 골라내는 조작이다. 예를 들어, 키를 재는 작업은 3차원에서 1차원의 정보를 사영하는 것에 해당된다.
우리가 물체를 바라볼 때도 비슷한 일이 일어나고 있다. 안구 안쪽에 있는 '망막'은 외부의 빛을 받아들이는 2차원의 스크린이다. 그 스크린에 물체의 상이 평면적으로 비치게 된다. 하지만 좌우의 안구는 떨어진 위치에 있기 때문에, 각 스크린에 비치는 2차원의 상은 같지 않다. 뇌는 좌우 망막에 비치는 상의 '어긋남'을 바탕으로 해서 깊이의 정보를 덧붙인다. 우리가 바라보는 3차원 상은 이렇게 뇌 속에서 재구성된 '간접적인 3차원 상'이다.
고대 그리스의 철학자인 '플라톤(Plato, 기원전 427~기원전 347)'이 기원전 360년에 저술한 '국가'에는 '동굴의 비유'라는 유명한 이야기가 있다. 동굴의 벽에 비치는 그림자만을 계속 바라보고 있는 죄수는 그림자야말로 세상의 모든 것이라 믿고, 그림자를 만들어 내는 입체의 모습을 모른 채 일생을 마칠 것이다. 플라톤은 그렇게 말한 뒤, 경험한 것만을 진실이라고 생각하는 인간도 이 죄수와 같다고 지적했다. 플라톤은 '우리는 그림자만 보고 있다'라고 말하면서, 벽에서 동굴 밖으로 시선을 돌려 '참된 앎'을 구하라고 설파했다. 그리고 그는 이 '참된 앎'을 '이데아(idea)'라고 불렀다. 플라톤의 이 말은 앞으로 살펴볼 우주는 몇 차원인지에 대한 수수께끼에 도전하는 데도 매우 중요한 의미를 지니고 있다.

5. 차원의 확장
5-1. 차원에 대한 유클리드의 정의
유클리드'의 '원론'에서는 3차원까지의 정의만 나와 있다. 높은 차원에서 낮은 차원으로 내려가는 유클리드의 방식에는 4차원 이상이 등장하지 않는다. 유클리드의 원론에는 다음과 같이 차원이 정의되어 있다.
- 입체의 끝은 면이다.
- 면의 끝은 선이다.
- 선의 끝은 점이다.
5-2. 차원에 대한 푸앵카레의 정의
하지만 수학의 세계에서는 차원은 얼마든지 있어도 상관없다. 형태를 다루는 수학인 '기하학(Geometry)'에서는 4차원 공간 등 무한의 차원을 나타낼 수 있다. 이 한계를 '역전의 발상'으로 넘어선 사람이 바로 프랑스의 수학자 '앙리 푸앵카레(Henri Poincare, 1854~1912)'이다. 푸앵카레는 유클리드의 정의를 뒤집어서 '차원'을 새롭게 정의했다. 그 내용은 다음과 같다.
- 끝이 '0차원(점)'이 되는 것을 '1차원(선)'이라고 한다.
- 끝이 '1차원(선)'이 되는 것을 '2차원(면)'이라고 한다.
- 끝이 '2차원(면)'이 되는 것을 '3차원(입체)'라고 한다.
- 끝이 '3차원(입체)'이 되는 것을 '4차원(초입체)'라고 한다.
'푸앵카레'의 정의는 낮은 차원에서 높은 차원으로 올라간다는 점에서 '유클리드'의 정의보다 낫다. 푸앵카레의 방법에 따르면, 4차원이나 5차원 등 얼마든지 많은 차원을 정의해 기하학에서 다룰 수 있다. 이리하여 많을 차원을 다루는 기하학이 크게 발전하게 되었다.
6. 초입체
6-1. 초정육면체
그러면 4차원 공간에 존재하는 '초입체(Hypercube)'란 무엇일까? 푸앵카레의 정의에 따르면, 끝이 3차원이 되는 것이 4차원이다. 따라서 '정육면체'를 움직이면, 4차원의 '초정육면체(정팔포체)'가 생긴다고 유추할 수 있다. 이것을 '4차원 정육면체' 또는 '테스랙트(tesseract)'라고 한다. 단, 정육면체를 움직이는 방향은 '3차원 공간안에 들어 있지 않은 방향(w축)'이어야 한다. 4차원 공간에서 x축, y축, z축 모두와 수직으로 만나는 방향이 w축이 된다.
그러면 초정육면체(정팔포체)는 어떻게 생겼을까? 선분은 두 개의 점으로 둘러싸여 있다. 정사각형은 4개의 선분으로 둘러싸여 있다. 정육면체는 6개의 '정사각형'으로 둘러싸여 있다. 이 사실로부터 우리는 4차원의 '초정육면체'는 8개의 정육면체로 둘러싸여 있다고 추측할 수 있다.
6-2. 초입방체(Hypercube)
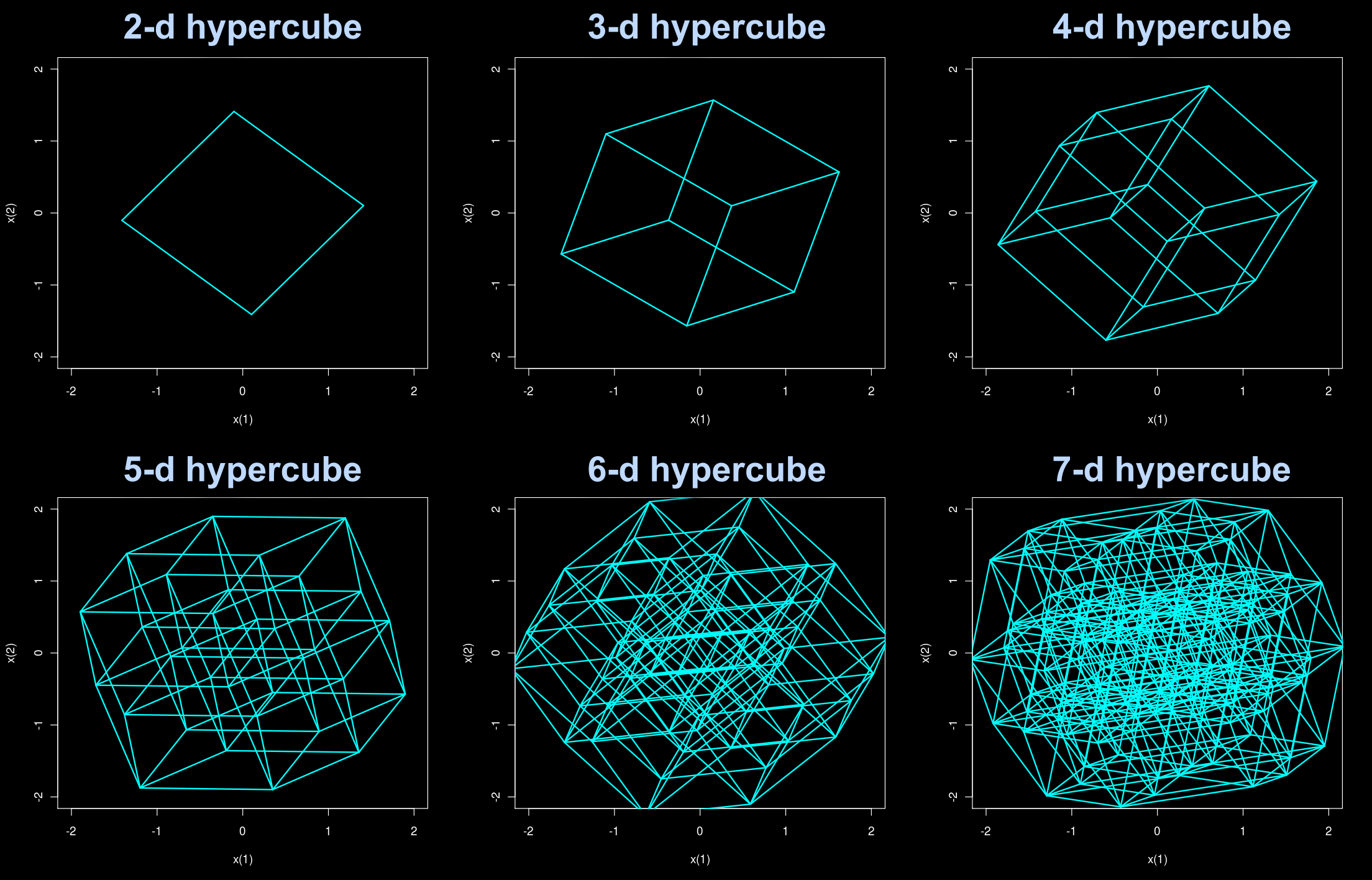
아래의 그림은 2차원의 정사각형, 3차원의 정육면체, 4차원의 '초정육면체(정팔포체)' 그리고 5~7차원의 '초입방체(Hypercube)'까지 그려 놓은 것이다. 물론 그림을 봐도 4차원 이상에 대해서는 잘 상상이 되지 않고, 잘 이해도 되지 않을 것이다. 하지만 너무 낙심할 필요는 없다. 2차원 공간에 있는 생물이 3차원 세상을 이해하기 어려운 것처럼, 3차원 공간에 살고 있는 인간이 4차원 이상의 초입방체 그림을 이해하기 어려운 것은 당연한 것이다.
6-3. 초정육면체의 전개도
지금까지는 '초정육면체'를 3차원 공간에 투영하는 것을 생각해 보았다. 이번에는 초정육면체의 전개도를 생각해 보자. 전개도란 어느 차원의 물체를 하나 아래의 차원으로 표현한 것이라고 할 수 있다. '정사각형(2차원)'을 절개하면 하나의 선분(1차원)이 생긴다. 정육면체(3차원)을 절개하면 6개의 정사각형(2차원)으로 이루어진 전개도가 된다. 초정육면체(4차원)을 절개하면 그 전개도는 8개의 정육면체(3차원)를 연결한 입체 도형이 될 것이다.
7. 낮은 차원에서 불가능한 일도 높은 차원에서는 가능하다.
2차원 평면과 3차원 공간을 생각해 보자. 2차원 평면에 'd'라는 글자가 있다. 이 글자를 180° 회전시키면 'p'가 된다. 그러면 'd'를 'b'로 만들 수 있을까? 2차원 공간에서는 아무리 돌려도 'd'를 'b'로 만들 수는 없다. 하지만 '3차원'을 이용하면 실현할 수 있다. 2차원 공간에서 'd'를 떼어 내 3차원 공간에서 뒤집어 'b'로 만들면 되기 때문이다.
이번에는 3차원 공간과 4차원 공간을 생각해 보자. 거울을 보면 당신의 얼굴과 몸은 좌우가 바뀌어 있을 것이다. 오른손은 왼손이 되고, 오른쪽 볼에 있는 점은 왼쪽 볼로 옮겨져 있을 것이다. 하지만 3차원 세계에서는 얼굴과 몸이 좌우가 바뀌는 것은 불가능하다. 하지만 4차원 공간으로 이동할 수 있다면, 얼굴을 좌우 바꿀 수 있다. 4차원 공간으로 들어 올려 거기서 회전시키면 오른손은 왼손이 되고, 오른쪽 볼에 있는 점은 왼쪽 볼로 옮겨질 것이다. 3차원 공간에서는 이해할 수 없는 불가사의한 현상이 4차원의 공간에서 일어난 것이다.
2차원 평면의 세계에서 감옥에 갇혀있는 죄수가 있다고 하자. 2차원 세계에서는 어떠한 방법으로도 탈출할 수 없는 감옥이다. 하지만 이 또한 3차원을 도입하면 이 죄수는 감옥을 쉽게 탈출할 수 있다. 3차원 공간으로 들어 올려, 거기서 바깥으로 빼내면 그만이기 때문이다. 인간이 높은 벽에 둘러싸여 갇혀 있으면 이를 뛰어넘지 못하지만, 하늘을 나는 새는 간단히 벽을 넘을 수 있는 것과 같다. 마찬가지로 3차원 감옥에 갇혀있는 죄수들도 4차원 공간을 이용할 수 있다면, 감옥을 쉽게 탈출할 수 있을 것이다.