현대 수학을 대표하는 분야 중에 '위상수학(Topology)'이라는 분야가 있다. '위상수학'이라고 하면, 약 100년의 세월을 거쳐 마침내 2006년에 해결된 엄청난 난제 '푸앵카레의 추측(Poincare Conjecture)'을 떠올리는 사람들도 있을 것이다. 과연 '위상수학'이란 어떤 학문이고, 또 수많은 수학자들을 사로잡은 '푸앵카레의 추측'은 무엇일까?
0. 목차
- '위상수학'이란 무엇인가?
- '위상수학'의 탄생
- 위상 동형
- '뫼비우스의 띠'와 '클라인의 병'
- '푸앵카레의 추측'이란?
- 다양한 분야에서 주목받는 '위상수학'

1. '위상수학'이란 무엇인가?
수학계의 노벨상이라고 불리는 '필즈상(Fields Medal)'은 수학계에서 가장 권위 있는 상이다. 4년에 한 번 현저한 업적을 남긴 40세 이하의 수학자에게 수여된다. 1936년에 만들어진 후, 2023년 현재 60명 이상의 수학자가 '필즈상'을 받았고, 2022년 7월에는 '허준이(1983~)' 교수가 한국인으로는 처음으로 필즈상을 수상했다. 이런 필즈상 수상자 가운데 특히 수상자가 많은 분야 가운데 하나가 '위상수학(Topology)'이다.
'위상수학(Topology)'는 기하학의 한 분야로, '토포스(Topos)'는 그리스어로 '위치'를 나타낸다. 직역하면 '위치의 학문'이 된다. '기하학'은 도형에 대해 연구하는 수학의 한 분야이다. 중고등학교에서 배우는 기하학은 변의 길이나 각도 등에 착안해 도형을 분류하고 각각의 성질을 괄한다. 그 기초가 되는 것은 '유클리드 기하학(Euclidean Geometry)'이다. 고대 그리스의 수학자 '유클리드(기원전 330?~275?)'가 기초를 세운 분야로, 여러 수학 분야 중에서도 가장 역사가 오래되었다고 한다. 그에 비해 '위상수학'의 역사는 미미하다. '위상수학'은 1700년대 후반 무렵에 탄생했다. '위치의 학문'인 '위상수학'은 '유클리드 기하학'과는 달리 '도형의 연결 방식'에 착안한다. 도형을 구성하는 점의 위치 관계에 착안해 도형의 성질을 생각하고 분류하는 것이다.
2. '위상수학'의 탄생
2-1. 쾨니히스베르크 다리 건너기 문제
'도형의 연결 방식'과 '점의 위치 관계'라고 말해도 도저히 감이 잡히지 않는 사람도 많을 것이다. 먼저 '쾨니히스베르크 다리 건너기 문제'를 예로 들어 '위상수학'의 기본 개념을 소개한다. 이 문제를 통해 스위스의 수학자 '레온하르트 오일러(Leonhard Euler, 1707~1783)'가 처음으로 '위상수학'의 개념을 알아냈다고 한다.
'레온하르트 오일러(Leonhard Euler)'가 활약한 시대에 유럽의 '발트해(Baltic Sea)' 남쪽 해안 '동프로이센(Ost Preussen, 옛 독일제국 북동부에 본토와 분리되어 있었던 영토)'에 '쾨니히스베르크(Königsberg)'라는 도시가 있었다. 현재는 러시아의 고립된 영토인 '칼리닌그라드(Калинингра́д, Kaliningrad)' 지역이다. 이 도시는 '쾨니히스베르크 대학교' 교수였던 철학자 '이마누엘 칸트(Immanuel Knat, 1724~1804)'가 생애를 보낸 곳으로도 알려져 있다. 이 도시의 중심에는 '발트해'로 흘러드는 큰 강이 있었다. 강 가운데의 모래톱에도 시가지가 형성되었으며, 모래톱 부근에는 7개의 다리가 있었다. 어느 날 누군가 '어떤 지점에서 출발해 다리 7개를 모두 1회씩 건너 원래의 지점으로 돌아올 수 있을까?'라는 문제를 던졌다. 이 문제에 대해 수학적인 해답을 제시한 사람이 바로 '레온하르트 오일러'이다.
이 문제에서 착안해야 할 점은 다리의 길이나 육지의 형태 등이 아니다. 중요한 것은 다리와 육지의 연결 방식이다. 그래서 오일러는 '쾨니히스베르크 거리'를 아래의 그림처럼 점점 간략화하면서 생각했다고 한다. 강으로 갈라진 육지를 각각 하나의 점으로 나타내고 그들을 잇는 다리를 선으로 나타낸 것이다. 이렇게 해서 '레온하르트 오일러'는 최초의 문제를' 어떤 하나의 점에서 출발해 모든 선을 한 번씩 지나 최초의 점으로 되돌아올 수 있는가?'라는 문제로 바꿨다. 이것은 '한붓그리기 문제'로 알려져 있다. '한붓그리기 문제'란 점과 선으로 그려진 도형을 하나의 이어진 선으로 중복하지 않고 그릴 수 있느냐 하는 문제이다.
1736년 '레온하르트 오일러'는 '한붓그리기로 최초의 점에 돌아오기 위한 조건은 모든 점에서 짝수 개의 선이 나오는 것'임을 증명했다. 도형이 한붓그리기 될 수 있는 필요충분조건을 수학적으로 밝힌 것이다. 쾨니히스베르크 거리를 간략화한 도형은 모든 점에서 홀수 개의 선이 나와 있다. 따라서 모든 다리를 한 번씩 건너서 원래의 지점으로 돌아올 수는 없다. '레온하르트 오일러'는 이 물음을 통해 다리의 연결 방식을 유지하면서도, '도형(이 경우는 지도)'을 변형시킨다는 아이디어를 얻었다.

2-2. 유연한 기하학 '위상수학'
'레온하르트 오일러' 이후 '위상수학'은 도형을 '신축(늘이거나 줄임)'시키는 등의 변형으로도 바뀌지 않는 도형의 성질을 생각하는 새로운 기하학으로 발전했다. 연구를 계승한 사람은 독일의 수학자 '카를 프리드리히 가우스(Carl Friedrich Gauss, 1777~1855)'와 '베른하르트 리만(Bernhard Riemann, 1826~1866)'이다. '위상수학'에서는 신축에 의해 도형을 변형시킬 때 무조건 도형을 자르거나 붙일 수는 없지만, 길이나 각도에서는 구애받지 않는다. 그 점에서 '위상수학'을 '유연한 기하학'이라고도 한다.
또 '레온하르트 오일러'가 다룬 '쾨니히스베르크의 다리'를 건너는 문제를 기원으로 하여, 유한 개의 점과 유한 개의 선으로 잇는 도형을 '유한 그래프(Finite Graph)'라고 한다. 이 그래프를 다룬 '그래프 이론(Graph Theory)'은 지금 컴퓨터 시뮬레이션과 '인공 지능(AI)' 등의 정보 과학을 비롯해 폭넓은 과학 분야에서 빼놓을 수 없는 이론이 되었다.
3. 위상 동형
3-1. 지하철 노선도
사실 '위상수학'은 매우 가까운 곳에서 발견할 수 있다. 바로 전철의 '노선도'이다. 노선도를 볼 때 우리는 노선끼리의 연결 방식에 주목한다. 이때 목적지까지의 실제 거리와 지리적 위치의 정확성에 신경을 쓰는 사람은 별로 없을 것이다. 이것은 바로 '위상수학(Topology)'의 생각이다.
3-2. 도넛과 커피 컵을 구별하지 않는 이유
더 구체적인 예를 들어 '위상수학'의 개념을 알아보자. '위상수학' 연구자들은 '구멍이 하나 뚫린 도넛' '손잡이 달린 커피 컵'을 구별하지 않는다는 점이다. '유클리드 기하학'에서 보면 당연히 '구멍이 하나 뚫린 도넛'과 '손잡이 달린 커피 컵'의 형태는 다르다. 그러나 '위상수학'에서는 도형을 연속적인 신축에 의해 변형할 수 있다. 여기서 중요해지는 것이 도형에 있는 '구멍'의 수이다. '구멍이 하나 뚫린 도넛'과 '손잡이 달린 커피 컵'에는 모두 구멍이 하나씩 있다. 커피를 담는 오목한 부분도 구멍처럼 생각되지만, 관통하고 있지 않으므로, '위상수학'에서는 구멍이라 생각하지 않는다.
'위상수학'에서는 연결 방식을 유지한 채 신축 등으로 도형을 변형시켜 형태가 일치하는 것은 모두 같은 도형으로 여긴다. 이것을 '위상 동형(Homeomorphic)'이라고 한다. '구멍이 하나 뚫린 도넛'과 '손잡이가 하나 있는 커피컵'은 신축시켜 같은 형태로 만들 수 있다. 즉, '위상수학' 세계에서는 둘은 같은 도형, 즉 '위상 동형'이다.
3-3. '위상수학'으로 문자를 분류해 보자.
이번에는 문자와 기호를 예를 통해 '위상수학'의 개념에 다가가 보자. 아래 박스에는 여러 가지 문자와 기호가 있다. 단, 여기에서 다루는 문자와 기호에는 '선의 굵기(폭)'이 있는 것으로 한다. 즉, 문자와 기호를 2차원 평면 도형으로 보고 '위상 동형(Homeomorphic)'인 것들끼리 묶어보자. 핵심은 앞에서 말한 '부품의 수'와 '각각의 부품이 가진 구멍의 수'이다. '구멍의 수'에 대해서는 더 이상 설명하지 않아도 될 것이다. '부품의 수'란 그 도형이 몇 개의 요소로 이루어졌는가 하는 것이다.
♥, ₩, *, ^, ㅇ, ㅠ, ㅛ, ㅗ, 七, ㄸ, ?, !, &, 二, 三, 五, 八, #, =, ♡, @, ㅃ, 品, &, 月, 日, 田, 用, %, Apple, 밥, 사랑, Chat GPT, Elon Musk, Saltlux, Furiosa, Singularity, Starship, Clinomics, Mac Book, Phython, 닭강정, 믿음, 양고기, 코딩, 미래, 우주, 특이점, 유튜브, BBQ, Google
- 구멍이 0개인 부품 1개: ♥, *, ^, ㅠ, ㅛ, ㅗ, 七
- 구멍이 0개인 부품 2개: ㄸ, ?, !, 二, =, 八
- 구멍이 0개인 부품 3개: 三
- 구멍이 1개인 부품 1개: ㅇ, 五, #, ♡, @
- 구멍이 1개인 부품 2개: ㅃ&=
- 구멍이 1개인 부품 3개: 品
- 구멍이 2개인 부품 1개: &, 月, 日
- 구멍이 4개인 부품 1개: 田, 用
- 구멍이 6개인 부품 1개: ₩
- 구멍이 0개인 부품 1개, 구멍이 1개인 부품 2개: %, 밥
- 구멍이 0개인 부품 1개, 구멍이 1개인 부품 4개: Apple
- 구멍이 0개인 부분 2개, 구멍이 1개인 부품 4개: Google
- 구멍이 0개인 부품 3개, 구멍이 1개인 부품 1개: 미래, 우주
- 구멍이 0개인 부품 3개, 구멍이 1개인 부품 3개: 믿음
- 구멍이 0개인 부품 4개, 구멍이 1개인 부품 1개: 사랑, 코딩
- 구멍이 0개인 부품 4개, 구멍이 1개인 부품 2개: 유튜브, Phython
- 구멍이 0개인 부품 5개, 구멍이 1개인 부품 2개: Chat GPT, 양고기
- 구멍이 0개인 부품 6개, 구멍이 1개인 부품 1개: Saltlux
- 구멍이 0개인 부품 6개, 구멍이 1개인 부품 2개: Furiosa, 특이점
- 구멍이 0개인 부품 7개, 구멍이 1개인 부품 2개: Starship, Elon Musk
- 구멍이 0개인 부품 8개, 구멍이 1개인 부품 2개: 닭강정
- 구멍이 0개인 부품 10개, 구멍이 1개인 부품 1개: Clinomics
- 구멍이 0개인 부품 11개, 구멍이 1개인 부품 2개: Singularity
- 구멍이 0개인 부품 3개, 구멍이 1개인 부품 3개, 구멍이 2개인 부품 1개: Mac Book
- 구멍이 1개인 부품 1개, 구멍이 2개인 부품 2개: BBQ
3-4. 불변량
위에서 예로 든 '쾨니히스베르크의 다리 건너기 문제'나 '노선도'의 경우는 '굵기가 없는 선'과 '크기가 없는 점'을 사용해 생각했다. 이 경우에는 점과 선의 연결 방식이 중요하다. 한편 '문자 분류'에서는 문자와 기호를 폭이 있는 2차원 평면 도형으로 생각해 '구멍의 수'와 '부품의 수'를 사용해 생각했다. 이처럼 '점과 점의 연결 방식', '구멍의 수', '부품의 수'처럼 도형을 변형해도 바뀌지 않고 남는 성질을 '불변량(invariant)'이라고 한다.
4. '뫼비우스의 띠'와 '클라인의 병'
4-1. 뫼비우스의 띠
'위상수학'에서 자주 등장하는 도형 중에 '뫼비우스의 띠'가 있다. 독일의 수학자 '아우구스트 페르디난트 뫼비우스(August Ferdinand Möbius, 1790~1868)'가 1858년 무렵에 발견한 '곡면(휘어진 면)'이다. '뫼비우스의 띠(Mobius strip)'란 가늘고 긴 띠를 180° 비틀어 끝과 끝을 연결한 것이다. 이 도형은 띠의 바깥쪽을 더듬어 가면, 안쪽으로 돌아갔다가 다시 바깥쪽으로 되돌아오는 기묘한 성질이 있다. 즉, 안과 밖이라는 개념이 없다. 무한히 더듬어 갈 수 있기 때문에 '무한대(∞)'를 상징하는 도형으로 사용되는 경우도 많다.
테이프의 끝과 끝을 비틀지 않고 그대로 연결한 '보통의 고리'와 '뫼비우스의 끈'을 '위상수학'에서 서로 다른 도형으로 여긴다는 것을 직감적으로 알 수 있을 것이다. 자르거나 붙이지 않는 한 어떻게 연속적으로 변형해도 '보통의 고리'를 '뫼비우스의 띠'로 만드는 것도, 반대로 '뫼비우스의 띠'를 '보통의 고리'로 만드는 것도 전혀 불가능하기 때문이다.

4-2. 클라인의 병
'뫼비우스의 띠'는 3차원 공간에 존재하는 도형인데, 이 뫼비우스의 띠를 더 발전시킨 사람이 등장했다. 독일의 수학자 '크리스티안 펠릭스 클라인(Christian Felix Klein, 1849~1925)'이다. '크리스티안 펠릭스 클라인'은 '클라인의 병(Klein Bottle)'이라는 물체를 생각했다. 실은 아래에 그림으로 제시한 클라인의 병은 가짜 '클라인의 병이다. 참된 '클라인의 병(Klein Bottle)'은 원기둥 양 끝의 변이 측면에 구멍을 만들지 않고 서로 합쳐지는 형태를 하고 있다. 즉, 측면에 구멍을 내지 않고 연결하려 했지만, 3차원 공간에서 '클라인의 병'을 실현하기란 불가능하기 때문에 어쩔 수 없이 이 구멍을 만들어 서로 연결한 것이다. 예컨대 4차원 공간에서라면 참된 '클라인의 병'을 실현할 수 있다.
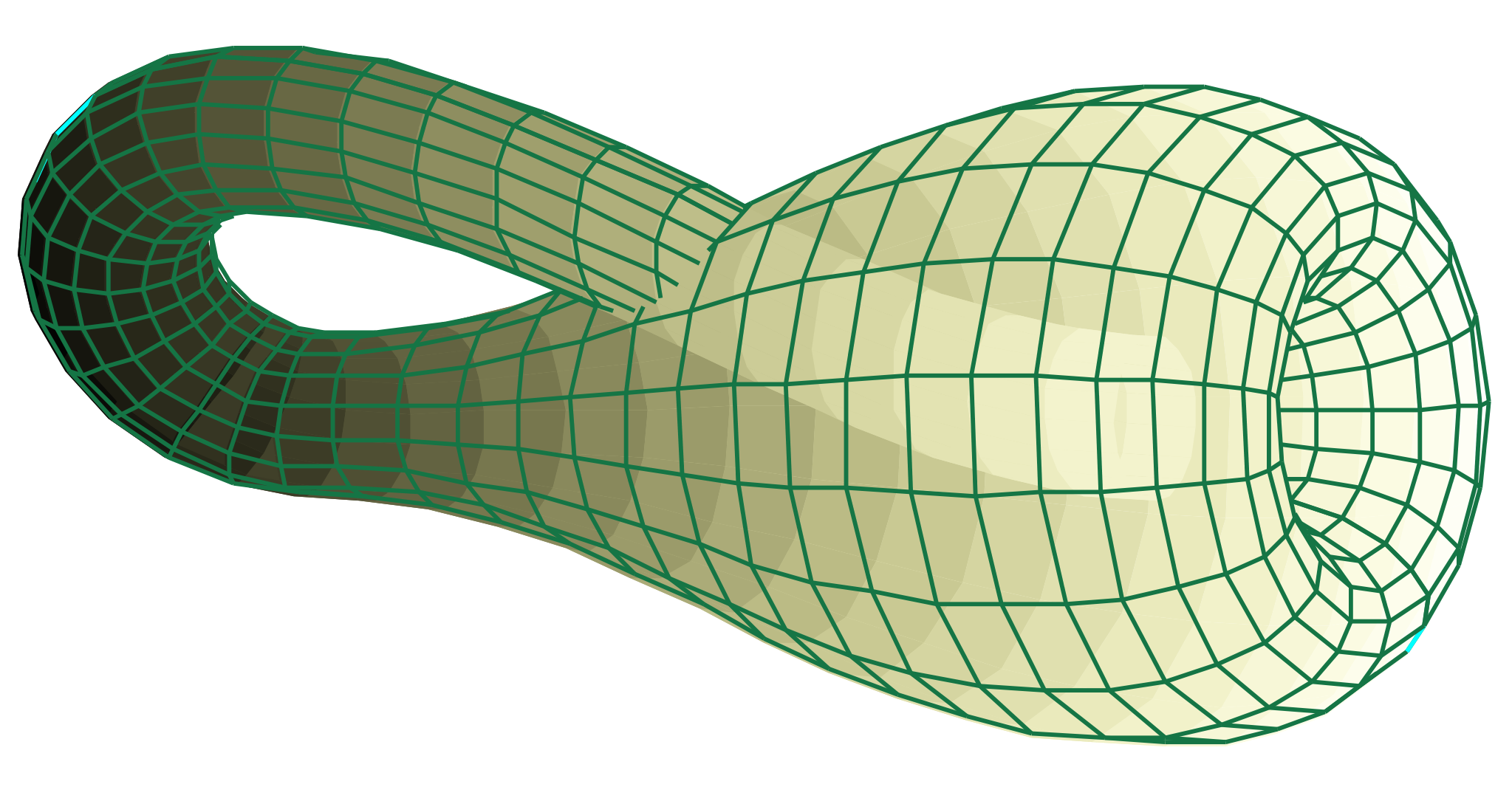
4-3. 폐곡면
그런데 3차원에서 '공의 표면'이나 '도넛 표면은' 곡면이 닫혀 있다. 즉, 무한히 가도 끝이 없다. 이러한 곡면을 '폐곡면(Closed Surface, 닫힌 곡면)'이라고 한다. '클라인의 병'의 표면도 무한히 가도 끝이 없으므로 '폐곡면(닫힌 곡면)'이다.
3차원 공간에 만들어진 '폐곡면'에는 '안과 밖(안쪽과 바깥쪽)'의 구별이 있다. 하지만 '클라인의 병'은 '폐곡면'인데도 불구하고 안과 밖의 구별이 없다는 특징이 있다. 이 점에서 '뫼비우스의 띠'와 '클라인의 병'은 아주 비슷하다. 이것은 '뫼비우스의 띠'나 '클라인의 병'이 가진 '위상수학(Topology)'적인 성질이다. 이처럼 안과 밖이 없는 닫힌 곡면은 실은 무한히 많은 종류가 있음이 알려져 있다.

5. '푸앵카레의 추측'이란?
'위상수학(Topology)'은 '쾨니히스베르크의 다리 건너기 문제'로 시작되어, 2차원, 3차원, 4차원, 그리고 더 고차인 n 차원 공간으로 연구가 확대되었다. 그중에서도 '위상수학'을 수학의 한 분야로 크게 발전시키는 토대를 만든 사람이 프랑스의 수학자 '앙리 푸앵카레(Henri Poincare, 1854~1912)'이다.
그리고 1904년에 그가 추측한 것이 그 유명한 '푸앵카레의 추측(Poincare Conjecture)'이다. '푸앵카레의 추측'이란 '위상수학'에서의 중요한 추측이며, 그 증명은 100년 가까이 많은 수학자들의 도전을 좌절시켰다. 2000년에는 미국의 '클레이 수학 연구소(CMI: Clay Mathematics Institute)'가 '푸앵카레의 추측'을 7개의 '밀레니엄 문제(Millennium Prize Problems)'의 하나로 선정하고 100만 달러의 현상금을 내걸었다. 그리고 2002년~2003년에 러시아의 '그리고리 페렐만(1966~)'이 증명에 성공하고, 2006년에 해결이 선언됨으로써 7개의 문제 가운데 유일하게 해결된 문제가 되었다.
'푸앵카레의 추측'은 그것을 푸는 것도 어렵지만, 수학 전문가가 아닌 사람은 이해하기조차 매우 어려운 문제이다. 그래서 여기에서는 '푸앵카레의 추측'이 제창되고 증명되기까지의 큰 흐름만 쫓아가 보기로 하자. '푸앵카레의 추측'을 문자로 간단히 말하면 다음과 같다. 아마 무슨 말인지 전혀 모르겠다고 느껴지겠지만, 겁먹지 말고 하나하나씩 의미를 따져나가보도록 하자.
'단일 연결'의 3차원 '폐다양체(닫힌 다양체)'는 '3차원 구면'과 '위상 동형'이다.
5-1. '다양체'란?
먼저 '다양체'가 무엇인지 알아보자. '다양체(Manifold)'란 간단히 말하면, 어떤 성질을 만족하는 도형이나 공간을 가리킨다. 여기서는 '전체 안의 일부는 인식할 수 있지만 전체상은 확실히 알지 못하는 도형이나 공간'으로 생각하자. 예컨대 우리는 지구라는 거대한 구면의 표면에 살아간다. 그러나 먼 옛날 사람들은 지구가 광대한 우주에 떠다니는 구체라는 것 따위는 상상할 수도 없었고, 그저 지구는 넓고 납작하다고 생각했을 것이다. 실제로 좁은 범위를 보면, 지구 표면은 납작한 면처럼 보인다. '위상수학' 세계에서는 지구와 같은 구체의 표면, 즉 구면은 '2차원 다양체'로 분류된다. 우리가 알고 있는 3차원 공간에서는 지구상에서 위치를 특정하려면 '위도', '경도', '해발 고도'의 3가지 값이 필요하지만, 지구의 표면에 한정하면 '위도'와 '경도' 2가지 값으로 충분하다. 지구 표면은 2차원이기 때문이기 때문이다.
'구면은 좌우·상하·전후 3가지 차원을 갖는 3차원 도형이 아닐까?'하고 생각하는 사람도 있을 것이다. 확실히 구면은 3차원 공간 안에 그려지지만, 이것은 바깥 공간이 3차원이라는 것이고, '위상수학'에서는 구면 그 자체는 '3차원 다양체'로 정의한다. '구면'이란 '구체 표면의 곡면'이며, 구체 내부는 포함하지 않는다는 것에도 주의해야 한다. 마찬가지로 우주도 다양체라 할 수 있다. 그러나 옛날 사람이 지구를 바깥쪽에서 바라볼 수 없었던 것처럼, 우리는 우주 전체를 우주 바깥쪽에서 바라볼 수 없다. 우주가 어떤 형태인지를 알 수 없는 것은 그 때문이다.
'닫힌 다양체'란 아주 대략적으로 말하면, 다양체 가운데 크기가 유한한 다양체를 가리킨다. 그러면 푸앵카레의 추측에 등장하는 '3차원 닫힌 다양체' 및 '3차원 구면'이란 어떤 도형일까? 지구 표면처럼 크기가 유한한 구면은 좁은 범위로 한정하면 '납작한 면처럼 보이는 도형(더 정확하게는 좁은 범위에서 점의 위치를 특정하는 데 2차원 좌표로 충분한 도형)'이므로 '2차원 닫힌 다양체'였다. 이것을 발전시켜 생각하면, 차원을 하나 높인 '3차원 닫힌 다양체'란 '크기가 유한이며 좁은 범위로 한정하면 3차원 공간처럼 보이는 도형'임을 추측할 수 있다.
이제 다시 차원을 하나 낮춘 '2차원 닫힌 다양체'에 대해 생각해 보자. '2차원 닫힌 다양체'란 이미 설명한 대로 크기가 유한이며, 좁은 범위로 한정하면 납작한 면처럼 면처럼 보이는 도형을 말한다. 그리고 '2차원 닫힌 다양체' 가운데 가장 단순한 구조를 가지는 구체의 표면을 특히 '2차원 구면'이라고 한다. 예컨대 '위상수학'에서는 '지구', '공', '주사위' 같은 입체의 표면은 모두 '2차원 구면'으로 똑같이 간주한다.

5-4. '단일 연결'이란?
이제 푸앵카레의 추측에 나오는 '단일 연결'의 의미를 생각해 보자. '단일 연결(Simply Connected)'이란 '어떤 도형에 끈을 걸어 그 끈을 끌어당겼을 때 반드시 어떤 한 점에 모을 수 있다.'는 것을 의미한다. '2차원 구면'과 '토러스(Torus, 도넛처럼 구멍이 1개 있는 입체 표면)' 사이에는 도형의 성질에 근본적인 차이가 있다. 그래서 '위상수학'에서는 이들을 다른 종류의 도형으로 분류한다. 그러면 '2차원 구면'과 '토러스'는 '단일 연결'일까? '2차원 닫힌 다양체'에 달라붙게 끈을 걸었을 때, 끈이 걸리지 않고 한점에 모이는지 아닌지로 다양체를 구별할 수 있다. 이처럼 '2차원 구면'과 '토러스'의 성질에는 차이가 있으며, 이 차이를 구별할 수 있다.
- '2차원 구면'은 '단일 연결'인가?: '2차원 닫힌 다양체'에 달라붙게 끈을 걸었을 때, 원래의 입체가 공이든 정육면체이든 불가사리 모양이든 '2차원 구면'과 위상동형인 한, 끈을 한 점에 모을 수 있다. '위상수학(Topology)'에서는 이러한 성질을 '단일 연결'이라고 한다. 단, 끈을 끌어당길 때 끈은 한순간도 구면 위에 떨어져서는 안 된다.
- '토러스'는 '단일 연결'인가?: '2차원 닫힌 다양체'에 달라붙게 끈을 걸었을 때, 원래의 입체가 공이든 정육면체이든 '토러스'와 위상동형인 경우, 끈을 거는 방식에 따라서는 끈을 한 점에 모을 수 없다. 아래 그림에 나타낸 토러스에 끈을 거는 2가지 방법으로는 어느 경우에도 끈을 한 점에 모을 수 없다. 이것은 구멍의 수가 2개 이상인 경우라도 마찬가지이다. 즉, 토러스처럼 구멍이 1개 이상 뚫린 '2차원 닫힌 다양체'는 '단일 연결'이 아니다.
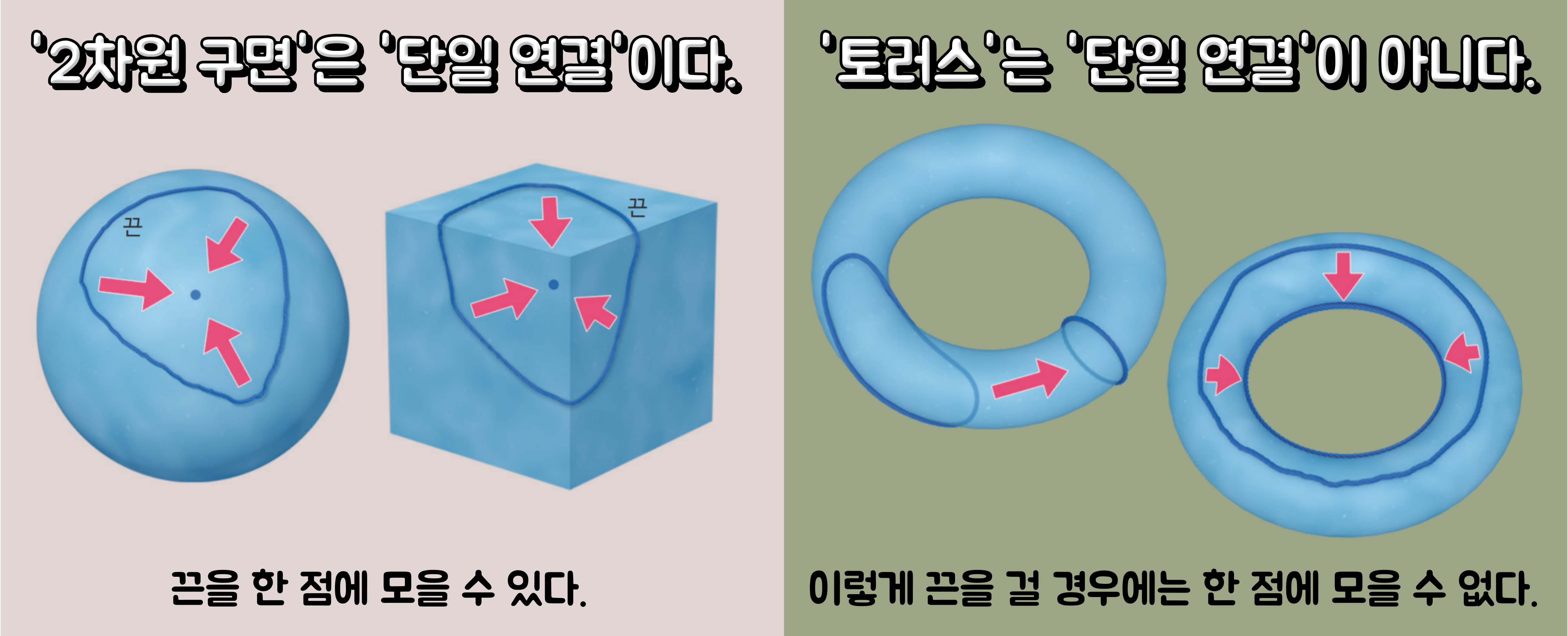
| - | 구멍의 수 | '단일 연결'인가? |
| 2차원 구면 | 0개 | 그렇다. |
| 토러스 | 1개 | 아니다. |
5-5. 푸앵카레의 추측(Poincare conjecture)
이제 '푸앵카레의 추측(Poincare conjecture)'이 무엇인지를 생각해 보자. 지금까지 이야기한 것처럼, 구멍이 뚫리지 않은 '2차원 닫힌 다양체'는 그것이 어떤 형태라도 끈을 회수해 한 점에 모을 수 있다. 즉 '단일 연결(Simply Connected)'이다. 또 반드시 2차원 구면으로 변형할 수 있으므로, '단일 연결'인 '2차원 닫힌 다양체'는 '2차원 구면'과 '위상동형'이라고 할 수 있다. 그리고 나아가 푸앵카레는 다음과 같이 고찰했다. '단일 연결'인 '2차원 닫힌 다양체'가 '2차원 구면'과 '위상 동형'이라는 성질은, 차원을 하나 높인 '3차원 닫힌 다양체'에서도 성립하지 않을까? 즉, '단일 연결'인 '3차원 닫힌 다양체'는 '3차원 구면'뿐이지 않을까? 이것이 바로 '푸앵카레의 추측'이며, '단일 연결인 3차원 닫힌 다양체는 3차원 구면과 위상 동형'임을 의미하는 것이다.
5-6. '기하화 추측'이 옳으면, '푸앵카레의 추측'도 옳다.
'3차원 닫힌 다양체'의 '위상수학(Topology)'적 분류는 '2차원 닫힌 다양체'보다 훨씬 복잡하다. 그래서 '앙리 푸엥카레(Henri Poincare)'는 살아 있는 동안 이 추측을 스스로 증명할 수 없었다. '푸앵카레의 추측'에 대해 그 후 많은 수학자가 증명에 도전했다. 그리고 '푸앵카레의 추측'으로부터 56년 후인 1960년에 '5차원 이상의 닫힌 다양체'에서, 이서 1982년에 '4차원 닫힌 다양체'에서 '푸앵카레의 추측'이 성립함이 증명되었다. 5차원 이상의 경우를 증명한 미국의 수학자 '스티븐 스메일(Stephen Smale, 1930~)'과 4차원의 경우를 증명한 미국의 수학자 '마이클 프리드먼(Michael Friedman, 1951~)'은 함께 그 업적이 인증되어 '필즈상(Fields Medal)'을 받았다. 수학에서는 저차원으로 생각하기보다 고차원으로 생각하는 편이 개념을 이해하기 쉬운 경우가 있다. 그 결과, 원래 푸앵카레의 추측인 3차원의 경우만 남게 되었다.
한편, 4차원의 푸앵카레 추측이 증명되었을 무렵, 미국의 수학자 '윌리엄 서스턴(1946~2012)'이 '기하화 추측(Geometrization Conjecture)'을 발표하였다. 이것은 '3차원 닫힌 다양체가 어떤 형태여도 반드시 8종류의 기본적인 다양체의 조합에 의해 구성될 것'이라는 추측이다. 그런데 3차원 구면은 '기하화 추측'에 등장하는 8종류 가운데 가장 단순한 구조를 가지는 '3차원 닫힌 다양체'이다. '윌리엄 서스턴(William Thurston)'의 '기하화 추측'이 옳으면, 단일 연결인 '3차원 닫힌 다양체'가 어떤 형태여도 '3차원 구면'과 '위상 동형'이 될 수 있음을 여러 수학자가 알아차렸다. 이것은 '기하화 추측'이 옳다고 증명되면, 필연적으로 '푸앵카레의 추측'의 옳음도 증명되는 것을 의미했다.
5-7. 100년만에 해결된 '푸앵카레의 추측'
이리하여 여러 수학자가 '기하화 추측'의 증명에 도전하기 시작했다. 그리고 그 가운데 미국의 수학자 '리처드 스트라이트 해밀턴(Richard Streit Hamilton, 1943~)'이 '리치 플로 방정식(Ricci flow Equation)'을 사용해 증명하는 방법을 찾아냈다. '리치 플로 방정식'은 열이 시간 경과와 더불어 서서히 확산하는 모습을 나타내는 '열전도 방정식(Heat Conduction Equation)'과 형태가 비슷하다. '리처드 스트라이트 해밀턴'은 이 '리치 플로 방정식'을 다양체에 적용하고 시간을 경과시킴으로써, 툭 튀어나오거나 움푹 팬 매우 복잡한 '3차원 닫힌 다양체'라도 그것을 서서히 고르게 만들어 멋진 형태로 성형할 수 있지 않을까 생각했다. '리처드 스트라이트 해밀턴'은 '기하화 예측'의 증명에 상당히 다가갔다. 그러나 큰 벽에 부딪혔다. '리치 플로 방정식'의 계산을 계속하면 '다양체가 아닌 도형(이것을 특이점이라고 한다)'이 나타났던 것이다.
그리고 드디어 이 '특이점(Singularity)'이 벽을 돌파한 사람이 나타났다. 바로 당시 상트페테르부르크 '스테클로프 수학 연구소'에 근무하던 '그리고리 페렐만(러시아어: Григо́рий Я́ковлевич Перельма́н, 1966~)'이다. '그리고리 페렐만'은 '특이점'이 발생하기 전에 그것을 찾아내 특이점이 되기 조금 앞서 다양체를 잘라내고, 분할한 각각의 다양체에서 '리치 플로 방정식'의 계산을 계속할 수 있는 방법을 연구했다. 그 결과, '윌리엄 서스턴'의 추측대로 '3차원 닫힌 다양체'가 8종류의 기본적인 다양체로 구성됨을 알아냈다. '그리고리 페렐만'은 연구 결과를 논문으로 정리해 2002년에 인터넷에 공개했다.
5-8. 필즈상을 거부하다.
그런데 사실은 그 논문에 '푸앵카레의 추측'이 직접 언급된 것은 아니었다. 그러나 곧 '푸앵카레의 추측'과 관련이 있음을 알아차린 수학자가 나타났고, 인터넷에 푸앵카레의 추측을 증명했다는 논문이 실렸다는 소문이 퍼졌다. 그 후, '매사추세츠 공과대학교(MIT: Massachusetts Institute of Technology)'의 수학자가 증명이 옳음을 확신하고 '그리고리 페렐만'에게 특별 강연을 의뢰했다. 2003년에는 MIT를 포함한 3개 대학에서 '그리고리 페렐만'의 특별 강연이 열렸다. 또 여러 세계 유수의 수학자 팀이 그 증명이 옳은지를 검증했다. 논문 내용이 난해하고 게다가 세부 기술이 생략되었기 때문에, 검증은 난항을 겪었다고 한다. 하지만 2006년에 드디어 여러 연구팀이 검증을 완료했다. 증명이 옳다는 것이 확인된 것이다. 약 100년에 걸친 수학자들의 도전에 종지부를 찍은 순간이었다.
증명이 옳다는 것이 증명되자 '필즈상'의 수여가 결정되었다. 하지만 놀랍게도 '그리고리 페렐만'은 수상을 거부하였다. 1936년 '필즈상' 창설 이후 처음으로 수상을 거부한 것이다. 나아가 2010년에는 '클레이 수학 연구소(CMI)'가 수여하는 '밀레니엄 문제(Millennium Prize Problems)'의 현상금 100만 달러의 수여도 거부했음이 알려졌다. '그리고리 페렐만'은 논문 발표와 2003년의 특별 강연 뒤 무슨 일인지, 수학계와의 접촉을 일절 끊어버렸다. 그러나 이러한 일들로 인해 '푸앵카레의 추측'은 수학계뿐만 아니라 일반인들에게도 널리 알려지게 되었다.
6. 다양한 분야에서 주목받는 '위상수학'
'앙리 푸앵카레(Henri Poincare)'가 확립한 '위상수학(Topology)'은 '푸앵카레의 추측'에 대한 수학자들의 도전의 역사와 함께 크게 발전했다. '필즈상 수상자 중에 '위상수학'과 관련된 수학자가 많은 것으로부터도, '위상수학'이 현대 수학에 얼마나 큰 영향을 미쳤는지 알 수 있다. 게다가 '위상수학'의 영향은 지금 수학에만 그치지 않는다. 예컨대 우주의 형태를 생각할 때 '위상수학'은 빼놓을 수 없는 도구가 된다. 그 밖에도 물리학·화학·생물학 등 다양한 분야에서 꼭 필요한 개념이 되었다. '유연한 기하학'으로 시작된 '위상 기하학'은 현대 과학의 다양한 분야에서 활용되고, 발전을 계속하고 있다.
6-1. 실제 우주는 어떤 모양인가?
우리는 3차원 우주 공간을 튀어나가 밖에서 우주의 형태를 바라볼 수 없다. 하지만 3차원 공간의 내부에 있으면서 우주의 형태를 아는 것이 불가능하지는 않다. 그 방법의 하나가 우주의 '곡률'을 측정하는 것이다. '곡률(Curvature)'이란 곡선이나 곡면, 또는 공간이 휘는 방식을 말한다. '관측 가능한 범위'에서는 우주가 어느 방향에서도 항상 똑같은 성질을 가진 것처럼 보인다. 그 경우의 우주의 형태는 곡률이 양인 경우 '닫힌 우주(Closed Universe)', 곡률이 0인 경우는 '평탄한 우주(Flat Universe)', 곡률이 음인 경우는 '열린 우주(Open Univese)'가 된다.
각각의 경우의 '2차원 다양체'를 그림으로 제시했다. '3차원 우주(3차원 다양체)'의 모습은 그림으로 나타낼 수 없지만, '위상수학'적으로는 분석되어 있다. 관측 데이터에 따르면, 우주의 '곡률(Curvature)'은 거의 0에 가깝다. 그러나 엄밀하게 곡률이 0인지 아닌지는 밝혀지지 않았으며, 결국 현시점에서 우주의 형태는 엄밀하게 밝혀지지 않았다.
6-2. 위상 물질(Topological Material)
2016년에는 '위상 상전이와 물질의 위상에 관한 이론적 발견'으로 '데이비드 사울레스(David Thouless, 1934~2019)', '프레더릭 덩컨 마이클 홀데인(Frederick Duncan Michael Haldane, 1951~)', 'J. 마이클 코스털리츠(J. Michael Kosterlitz, 1942~)' 등 3명의 물리학자가 노벨 물리학상을 받았다. 물질은 조건에 따라 '기체', '액체', '고체' 등 분명하게 서로 다른 상태를 취한다. 이러한 물질의 상태를 '상(Phase)'이라 하고, 상이 바뀌는 것을 '상전이(Phase Transition)'라고 한다. 3명은 '위상수학'의 이론을 사용함으로써 '초전도체(Superconductor)'와 '초유도체(Superfluid)' 등 특수한 물질의 상을 연구하고, 그 성질을 이론적으로 해명했다.
이 연구가 발단이 되어 '위상 초전도체(Topological Superconductor)'나, 안쪽은 전기를 통하지 않는 반면에 표면은 전기를 잘 통하는 '위상 절연체(Topological Insulator)', '위상 반금속(Topological Semimetal)' 등에 대한 연구가 활발하게 이루어졌다. 이들을 총칭해 '위상 물질(Topological Material)'이라고 하며, 지금은 전자 장치를 고성능화하기 위한 열쇠를 쥔 물질로서 가장 주목받는 존재가 되었다.
'위상 물질(Topological Material)'은 '양자 컴퓨터(Quantum Computer)'를 혁명적으로 진보시킬 가능성도 감추고 있다. 양자 컴퓨터에서는 '양자 비트(Quantum Beat)'라는 정보 단위를 사용해 고속으로 계산을 처리하는데, 그러기 위해서는 '양자 비트'끼리 결합하는 '양자 얽힘(Quantum Entanglement)'이라는 물리 현상을 이용해야 한다. 그때 '위상 구조'라는 특수한 구조로 만들면 열의 영향을 받기 쉬운 '전자(Electron)' 같은 '양자(Quantum)'도, '양자 얽힘'을 안정적으로 유지할 수 있음이 밝혀졌다.
6-3. 매듭 이론(Knot Theory)
그 밖에도 '위상수학'에서 발전한 분야 중에 '매듭 이론'이라는 것이 있다. '매듭 이론(Knot Theory)'은 생물학에서 유전 정보를 담당하는 물질인 'DNA'의 형상 변화 메커니즘을 규명하는 데 도움이 되고 있다.