0. 목차
- '소수'란 무엇인가?
- '소수'에 규칙성은 없다?
- 소수 찾기
- 소인수 분해
- 소수는 무한한가?
- 메르센 소수
- 소수와 관계된 미해결 문제

1. '소수'란 무엇인가?
'소수(Prime Number)'란 1보다 크고, 1보과 자기 자신을 제외한 다른 수로는 나누어지지 않는 수를 말한다. 1, 2, 3, 4, 5...로 계속되는 양의 정수를 '자연수'라고 하며, 물건을 헤아리거나 순서를 나타낼 때 사용한다.
1과 소수 이외의 자연수는 모두 소수의 곱셈으로 나타낼 수 있다. 예컨대 30은 2×3×5이다. 게다가 곱하는 차례를 고려하지 않으면 그 방법은 1개밖에 없다. 그래서 소수를 '수의 원자'라고도 한다. 그리고 소수 이외의 수는 자연수는 '1과 그 자신 이외의 수를 약수로 가지는 자연수'로 '합성수(Composite Number)'라고 한다.
2. '소수'에 규칙성은 없다?
작은 수부터 소수를 찾아 나갈 때, 그것을 나타내는 데 규칙이 있을까? 지금까지 알려진 바에 따르면, 소수의 등장 방식은 매우 불규칙해 종잡을 수가 없다. 수많은 수학자들이 소수의 규칙을 찾아내려고 노력했지만, 그 규칙성을 찾아내지 못했다.
소수는 고대 그리스의 수학자 '유클리드'가 약 2300년 전에 쓴 '원론'에도 적혀 있다. 이처럼 오래전부터 연구되고 있음에도 불구하고, 현재까지도 소수의 완전한 규칙성은 발견되지 않았다. 그러면 소수에는 정말 규칙성이 없는 것일까?
2-1. '플리치타'의 '소수원'
아래의 그림은 '피터 플리치타(Peter Plichta)'의 '소수원(Prime Number Cross)'이라는 것이다. 숫자를 시계 방향으로 원처럼 나열해 갈 때 1부터 순서대로 나열하면서, 24마다 한 줄 밖의 원으로 이동하도록 배치되어 있다. 소수는 붉은색으로 나타냈다.
얼핏 보고도 알 수 있듯이, 2와 3을 제외하면 소수는 중심에서 바깥을 향해 어떤 특정 방사상의 선 위에 있으며, 다른 직선 위에는 나타나지 않는다. 이것으로 미루어 보면, 소수에 어떤 규칙성이 있는 것처럼 보인다. 하지만 소수를 나타내는 각각의 직선에 주목하면, 각 직선에서 소수가 나타나는 방식은 불규칙함을 알 수 있다. 거기에는 규칙성이 전혀 없는 것처럼 보인다. 이처럼 '피터 플리치타'의 소수원에서 소수의 불가사의함을 엿볼 수 있다.

3. 소수 찾기
3-1. 에라토스테네스의 체
그러면 소수를 발견하려면 어떻게 해야 할까? 소수를 확실하게 찾는 유일한 방법은 '에라토스테네스의 체(Eratosthenes' sieve)'이다. '에라토스테네스의 체'는 고대 그리스의 수학자 '에라토스테네스(기원전 175경~기원전 194경)'가 생각해냈다고 한다.
이 방법에서는 먼저 2 이상의 수를 적어 나열한다. 무한히 나열하는 것은 불가능하므로, 적당한 수까지 적어두도록 하자. 그다음 맨 앞의 2를 그대로 두고, 그 뒤에 오는 2의 배수를 없앤다. 남은 수 가운데 2 다음에 오는 것은 3이다. 그리고 그 3을 그대로 두고, 3의 배수를 없앤다. 이어 남은 수의 맨 앞의 5이므로... 같은 방법으로 계속해 간다. 그렇게 하면 최종적으로 남은 수는 소수가 된다. 이 방법은 매우 단순하지만 현재로서는 확실하게 소수를 발견하는 이 이상의 방법은 없다. 아래의 그림에서 '에라토스테네스의 체'라는 방법을 이용하여 실제로 1000까지의 소수를 구해보자.
- 먼저 2부터 100까지 적어둔다.
- 2를 제외하고 2의 배수를 제거한다.
- 3을 제외하고 3의 배수가 되는 수를 제거한다.
- 5를 제외하고, 5의 배수가 되는 수를 제거한다.
- 7을 제외하고, 7의 배수가 되는 수를 제거한다.
- 11을 제외하고, 11의 배수가 되는 수를 제거한다.
- 13을 제외하고, 13의 배수가 되는 수를 제거한다.
- 17을 제외하고, 17의 배수가 되는 수를 제거한다.
- 19를 제외하고, 19의 배수가 되는 수를 제거한다.
- 이것을 반복한다. 이리하여 마지막에 남은 것들이 소수이다.
3-2. 소수를 발견하는 공식들
'피터 플리치타(Peter Plichta)'의 '소수원(Prime Number Cross)'에서는 어떤 규칙성 같은 것도 보였다. 하지만 완전한 규칙성을 드러나지 않았다. 따라서 소수의 규칙성을 발견해 모든 소수를 구할 수 있는 공식을 유도하는 것은 수학자들의 꿈이다. 그런데 모든 소수는 무리이지만, 일부 소수를 발견할 수 있는 식은 몇 가지 알려져 있다.
독일의 수학자 '레온하르트 오일러(1707~1783)'는 '어떤 수와 그보다 1큰 수를 곱하고, 거기에 41을 더한 것이 소수가 된다.'는 사실을 발견했다. '어떤 수'를 n이라고 하고 식으로 나타내면 n×(n+1)=41이 된다. 예컨대 '어떤 수'를 5라고 하면, 5×(5+1)=71이며, 이것은 소수이다. 그러나 '어떤 수'가 무엇이든지 소수가 되는 것은 아니다. 예를 들어 40일 때는 40×(40+1)=1681이 된다. 1681은 41로 나눌 수 있으므로 소수가 아니다. 오일러가 발견한 식으로는, n이 0~39에서는 연속해서 소수를 만들어 낼 수 있다. n이 40일 때는 (40×41)+41=1681이 되어 소수가 아니다.
그리고 오일러가 발견 방식 외에도 소수의 일부를 만들어내는 식이 많이 발견되어 있다. 다음은 소수의 일부를 만들어 내는 다른 식들을 나열한 것이다. 그러나 이들도 반드시 소수가 되는 것은 아니어서 n의 값에 따라서는 소수가 되지 않는다.
- 4×n×(n+1)+59
- n×(n-79)+1601
- 4n2+170n+1847
- n2+n+17
- 2n2+29
- 2n2+2n+19
4. 소인수 분해
'합성수(1과 그 자신 이외의 수를 약수로 가지는 자연수)'를 소수의 곱셈으로 나타내는 것을 '소인수 분해(Prime Factorization)'라고 한다. 이른바 수를 '원자'로 분해하는 것이다. 소인수 분해는 그 수를 나눌 수 있는 소수를 찾아나가는 작업이다. 먼저 작은 소수로 나누어보고, 나누어떨어지면, 더 큰 소수로 나누어 본다. 이것을 차례로 계속하다가 마지막으로 소수가 남으면 끝난다.
그런데 '소인수 분해'는 비교적 작은 수에서는 문제가 없지만, 큰 수가 될수록 소인수 분해는 기하급수적으로 어려워진다. 왜냐하면 작은 수로는 나누어떨어지지 않는 것이 나오는 경우가 있기 때문이다. 즉, 큰 소수를 찾지 않으면 안 된다. 큰 소수를 찾으려면 기본적으로 '에라토스테네스의 체'를 사용하는 수밖에 없다. 거대한 수가 되면 심지어 컴퓨터를 사용해도 엄청난 시간이 걸린다.

4-1. RSA 암호
'RSA 암호'는 거대한 2개의 소수를 곱한 수를 '열쇠'로 해서 중요한 정보를 암호화하는 것이다. 열쇠가 어떤 소수를 곱한 것인지 알지 못하면, 암호화된 정보를 해독할 수 없다. 거대한 수의 '소인수 분해'를 단시간에 하는 것은 불가능하므로, 바탕이 되는 소수를 아는 사람 이외에는 해독할 수 없는 것이다. 예컨대 1611373를 1597×1009로 소인수분해를 하는 것은 매우 어렵다. 이보다 훨씬 큰 수를 소인수분해하기란 훨씬 어려울 것이다.
RSA 암호는 인터넷 쇼핑 등에서 남에게 알려지지 않고 신용 카드 번호를 송신하는 메커니즘이나, 시청료를 지불한 사람만이 볼 수 있는 텔레비전 방송 등 다양한 곳에서 이용되고 있다.
5. 소수는 무한한가?
5-1. 소수는 무한히 존재한다.
그러면 소수의 개수는 무한할까? 발견된 소수의 뒤에는 반드시 더 큰 소수가 나타난다. 즉, 소수는 무한히 존재한다. 이에 대한 답은 2300년 전 '유클리드(Euclid, 기원전 330~기원전 275)'의 '원론(Stoicheia)'에 이미 적혀있다. '유클리드(Euclid)'는 '원론'에서 아래와 같이 '소수가 무한히 존재함'을 증명하였다.
- 다른 소수 q1, q2, q3, ······, qn을 써서 다음과 같은 수 N을 만들 수 있다.
- N=q1×q2×q3······qn+1
- 이 수 N은 q1,q2,q3, ······, qn의 어느 소수로도 나누어떨어지지 않는다. 왜냐하면 어느 소수로 나누더라도 q1×q2×q3······×qn의 부분은 나누어떨어지지만 1이 남기 때문이다. (가장 작은 소수는 2)
- 따라서 N은 q1, q2, q3, ······, qn과 다른 소수이든가, 또는 q1, q2, q3, ······, qn이 아닌 다른 소수로 나누어떨어져야 한다.
- 따라서 q1,q2,q3, ······, qn 이외에 새로운 소수 qn+1이 있다.
- 이것을 되풀이하면, 차례로 새로운 소수 qn+2, qn+3, qn+4 ······가 발견될 것이다.
- 즉, 소수는 무한히 있음을 알 수 있다.
5-2. 소수가 출현하는 빈도는 점차 줄어든다.
소수는 무한히 존재하겠지만, 언제 나타날지는 예측할 수 없다. 소수는 파악할 수 없는 것처럼 보이지만, 그 성질을 아는 방법이 전혀 없는 것은 아니다. 커다란 수까지 소수를 계속 찾아나가다 보면, 어떤 것을 알아차리게 본다. 수를 100씩 구획해 각 구간에 몇 개의 소수가 있는지 세어 본다. 그러면 큰 수가 됨에 따라 소수가 등장하는 빈도가 적어진다는 사실을 알 수 있다. 그러면 소수는 어느 정도의 비율로 줄어들까? 반대로 말하면, 소수는 어떤 빈도로 나타날까? 그 상세한 성질을 알면 소수를 발견하는 공식에 가까워질 것이다. 이 문제에 가장 먼저 파고든 사람은 대천재로 알려진 독일의 수학자이자 물리학자인 '카를 프리드리히 가우스(Carl Friedrich Gauss, 1777~1855)'이다.
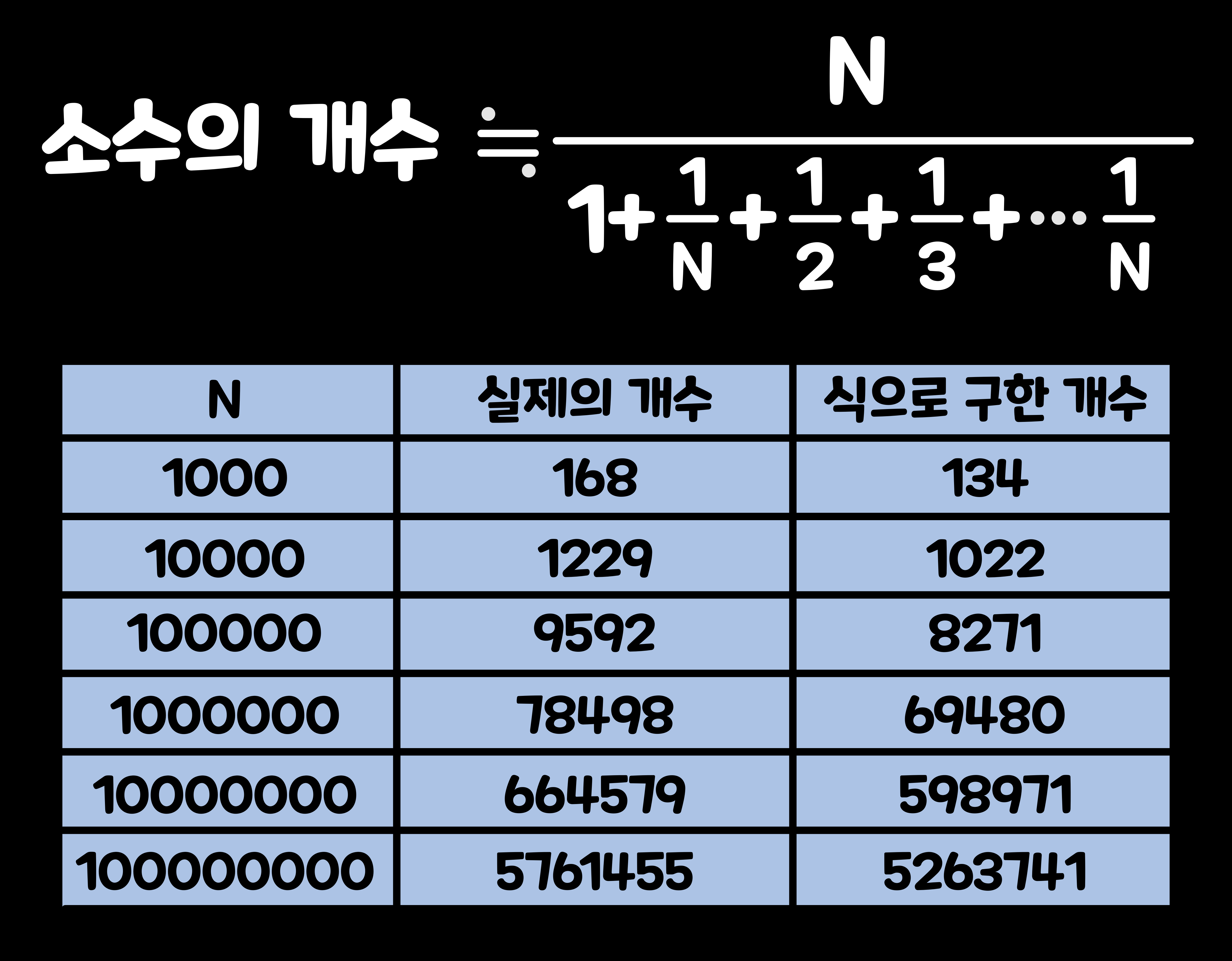
가우스는 15세 때 수를 1000씩 구획하고, 그 안에 나타나는 소수의 개수를 끈질기게 세었다. 어떤 사람에게 쓴 편지에서 가우스는 매일 한가한 시간의 15분 동안 소수의 수를 조사하고, 100만까지 이르지 않았을 때 그만두었다고 적었다. 그래도 수십만이나 되는 수를 조사한 가우스는 마침내, 처음부터 순서대로 세지 않더라도 어느 수까지 나타나는 소수의 개수를 대강 알 수 있는 소수 정리(Prime Number Theorem)'라고 불리는 식을 발견했다. 이 식으로 아주 정확한 수를 분명히 말할 수는 없는 것이다. 큰 수가 될수록 정확성은 증가하지만, 완전히 올바른 개수를 나타낼 수는 없다. 그렇지만 소수가 완전히 불규칙하게 나타나는데도 그 대략의 개수를 간단한 식으로 나타낼 수 있다는 사실은 신비롭지 않을 수 없다.
가우스는 이 식을 증명하지는 않았으나, 나중에 다른 수학자에 의해서 몇 가지 방법으로 증명되었다. 그리고 현재는 가우스가 발견한 것보다 더 정확하게 소수의 개수를 나타낼 수 있는 식도 발견되어 있다. 독일의 수학자 '베른하르트 리만(Bernhard Riemann, 1826~1866)'도 이 소수 정리의 증명을 시도했던 사람이다. '리만'은 1859년에 '주어진 수보다 작은 소수의 개수에 대해'라는 논문을 발표하고, 어떤 가정 아래 소수 정리를 증명했다. 그 가정을 '리만 추측ㅇ'라고 한다. '리만 추측'이 옳으면 소수 정리를 증명할 수도 있지만, 현재도 '리만 추측'이 옳은지는 해결되지 않은 채 남아 있다.
6. 메르센 소수(Mersenne number)
'메르센 수(Mersenne number)'는 2n-1 형태의 수를 말하며, M(n)으로 표기한다. 예컨대 M(10)=1023이다. '메르센 소수(Mersenne prime)'는 메르센 수 중 '소수(Prime Number)'인 것을 말한다. 따라서 M(n)이 소수면 n도 소수이다. 하지만 역으로 n이 소수라고 해서 항상 M(n)도 소수가 되는 것은 아니다. 아주 큰 '메르센 소수'는 컴퓨터를 통해 발견되어 왔다. 지금까지 발견된 '메르센 소수'를 정리하면 다음과 같다. (사이에 아직 메르센 소수가 존재할 가능성이 남아있는 것은 번호에 *표시를 붙였음)
| 번호 | n | 발견시기 | Discovered By | Method / Hard Ware |
| 1 | 2 | 기원전 500 | Ancient Greek Mathematicians | - |
| 2 | 3 | 기원전 500 | Ancient Greek Mathematicians | - |
| 3 | 4 | 기원전 500 | Ancient Greek Mathematicians | - |
| 4 | 7 | 기원전 500 | Ancient Greek Mathematicians | - |
| 5 | 13 | 1456 | Anonymous | Trial division |
| 6 | 17 | 1588 | Pietro Cataldi | Trial division |
| 7 | 19 | 1588 | Pietro Cataldi | Trial division |
| 8 | 31 | 1772 | Leonhard Euler | Enhanced trial division |
| 9 | 61 | 1883 | Ivan Mikheevich Pervushin | Lucas Sequences |
| 10 | 89 | 1911 Jun | R. E. Powers | Lucas Sequences |
| 11 | 107 | 1914 Jun 11 | R. E Powers | Lucas Sequences |
| 12 | 127 | 1876 Jan 10 | Édouard Lucas | Lucas Sequences |
| 13 | 521 | 1952 Jan 30 | Raphael M. Robinson | L-L / SWAC |
| 14 | 607 | 1952 Jan 30 | Raphael M. Robinson | L-L / SWAC |
| 15 | 1,279 | 1952 Jun 25 | Raphael M. Robinson | L-L / SWAC |
| 16 | 2,203 | 1952 Oct 07 | Raphael M. Robinson | L-L / SWAC |
| 17 | 2,281 | 1952 Oct 09 | Raphael M. Robinson | L-L / SWAC |
| 18 | 3,217 | 1957 Sep 97 | Hans Riesel | L-L / BESK |
| 19 | 4,253 | 1961 Sep 08 | Alexander Hurwitz | L-L / IBM 7090 |
| 20 | 4,423 | 1961 Nov 03 | Alexander Hurwitz | L-L / IBM 7090 |
| 21 | 9,689 | 1963 May 11 | Donald B. Gillies | L-L / ILLIAC II |
| 22 | 9,941 | 1963 May 16 | Donald B. Gillies | L-L / ILLIAC II |
| 23 | 11,213 | 1963 Jun 02 | Donald B. Gillies | L-L / ILLIAC II |
| 24 | 19,937 | 1971 Mar 04 | Bryant Tuckerman | L-L / IBM 360/91 |
| 25 | 21,701 | 1978 Oct 30 | Landon Curt Noll & Laur Nickel | L-L / CDC Cyber 174 |
| 26 | 23,209 | 1979 Feb 09 | Landon Curt Noll | L-L / CDC Cyber 174 |
| 27 | 44,497 | 1979 Apr 08 | Harry Lewis Nelson & David Slowinski | L-L / Cray 1 |
| 28 | 86,243 | 1982 Sep 25 | David Slowinski | L-L / Cray 1 |
| 29 | 100,503 | 1988 Jan 28 | Walter Colquitt & Luke Welsh | L-L / NEC SX-2 |
| 30 | 132,049 | 1983 Sep 19 | David Slowinski | L-L / Cray X-MP |
| 31 | 216,091 | 1985 Sep 01 | David Slowinski | L-L / Cray X-MP/24 |
| 32 | 756,839 | 1992 Feb 19 | David Slowinski & Paul Gage | L-L / Maple on Harwell Lab Cray-2 |
| 33 | 859,433 | 1994 Jan 04 | David Slowinski & Paul Gage | L-L / Cray C90 |
| 34 | 1,257,787 | 1996 Sep 03 | David Slowinski & Paul Gage | L-L / Cray T94 |
| 35 | 1,398,269 | 1996 Nov 13 | GIMPS / Joel Armengaud | L-L / Prime95 on 90 MHz Pentium PC |
| 36 | 2,976,221 | 1997 Aug 24 | GIMPS / Gordon Spence | L-L / Prime95 on 100 MHz Pentium PC |
| 37 | 3,021,377 | 1998 Jan 27 | GIMPS / Roland Clarkson | L-L / Prime95 on 200 MHz PentiumPC |
| 38 | 6,972,593 | 1999 Jun 01 | GIMPS / Nayan Hajratwala | L-L / Prime95 on 350 MHz Pentium PC |
| 39 | 13,466,917 | 2001 Nov 14 | GIMPS / Michael Cameron | L-L / Prime95 on 800 MHz Pentium PC |
| 40 | 20,996,011 | 2003 Nov 17 | GIMPS / Michael Shafer | L-L / Prime95 on 2 Ghz Dell Dimension |
| 41 | 24,036,583 | 2004 May 15 | GIMPS / Josh Findley | L-L / Prime95 on 2.4GHz Pentium 4 PC |
| 42 | 25,964,951 | 2005 Feb 18 | GIMPS / Martin Nowak | L-L / Prime 95 on 2.4 GHz Pentium 4 PC |
| 43 | 30,402,457 | 2005 Dec 15 | GIMPS / Curtis Copper & Steven Boone | L-L / Prime 95 on 2 GHz Pentium 4 PC |
| 44 | 32,582,657 | 2006 Sep 04 | GIMPS / Curtis Copper & Steven Boone | L-L / Prime 95 on 2.4 GHz Pentium 4 PC |
| 45 | 37,156,667 | 2008 Sep 06 | GIMPS / Hans-Michael Elvenich | L-L / Prime95 on 2.83 GHz Core 2 Duo PC |
| 46 | 42,643,801 | 2009 Jun 04 | GIMPS / Odd M. Strindmo | L-L / Prime95 on 3 GHz Core 2 PC |
| 47 | 43,112,609 | 2008 Aug 23 | GIMPS / Edson Smith | L-L / Prime95 on Dell Optiplex 745 |
| 48 | 57,885,161 | 2013 Jan 25 | GIMPS / Curtis Cooper | L-L / Prime95 on Intel Core2 Duo E8400 @3.00GHz |
| 49* | 74,207,281 | 2016 Jan 07 | GIMPS / Curtis Cooper | L-L / Prime95 on Intel i7-4790 @3.60GHz |
| 50* | 77,232,917 | 2017 Dec 26 | GIMPS / Jon Pace | L-L / Prime95 on Intel i5-6600 @ 3.30GHz |
| 51* | 82,589,933 | 2018 Dec 07 | GIMPS / Patrick Laroche | L-L / Prime95 on Intel i5-4590T @2.0GHz |
7. 소수와 관계된 미해결 문제
소수의 공식이나 개수 문제 뿐만 아니라, 소수와 관계된 미해결 문제는 이 밖에도 많이 남아있다.
7-1. 쌍둥이 소수(Twin Prime)
그중 하나는 '쌍둥이 소수(Twin Prime)'에 관한 것이다. '쌍둥이 소수'란 3과 5, 3와 7, 11과 13처럼 어떤 소수와 2의 차로 늘어선 소수 2개의 짝이다. 쌍둥이 소수가 나타나는 빈도는 수가 커지면 커질수록 줄어들어 드물어진다. 그런데 아주 큰 수가 되어도 쌍둥이 소수는 가끔 나타난다. 그러면 쌍둥이 소수는 무한히 존재하는 것일까? 2011년 12월에 발견된 쌍둥이 소수는 20만 700자리나 된다고 한다. 이 거대한 소수는 'Prime Grid'라 불리는 분산 컴퓨팅 프로그램으로 발견되었다. 그러나 앞으로 더욱 큰 쌍둥이 소수가 계속 발견될지는 알 수 없다. 쌍둥이 소수가 무한히 있을지도 모르지만, 아직 정확하게 증명되지는 않았다.
'쌍둥이 소수' 외에 '사촌 소수'라는 것도 있다. '사촌 소수(Cousin Prime)'는 4의 차로 늘어선 소수 2개의 쌍이다. 예컨대 3과 7, 13과 17, 등이다. 또 어떤 소수와 6의차로 늘어선 소수 2개의 쌍은 '섹시 소수(Sexy Prime)'라고 불린다. 예컨대 5와 11, 7과 13, 11과 17 등을 말한다.
| 소수 쌍 이름 | 차이 |
| 쌍둥이 소수(Twin Prime) | 차이가 2인 두 소수의 쌍 |
| 사촌 소수(Cousin Prime) | 차이가 4인 두 소수의 쌍 |
| 섹시 소수(Sexy Prime) | 차이가 6인 두 소수의 쌍 |
7-2. 골드바흐의 추측
'4 이상의 짝수는 모두 2개의 소수의 덧셈으로 나타낼 수 있다.'라는 미해결 추측도 있다. 이것은 독일의 수학자 '크리스티안 골드바흐(Christian Goldbach, 1690~1765)'가 제시한 추측으로, '골드바흐의 추측(Goldbach's Conjecture)'이라고 한다.
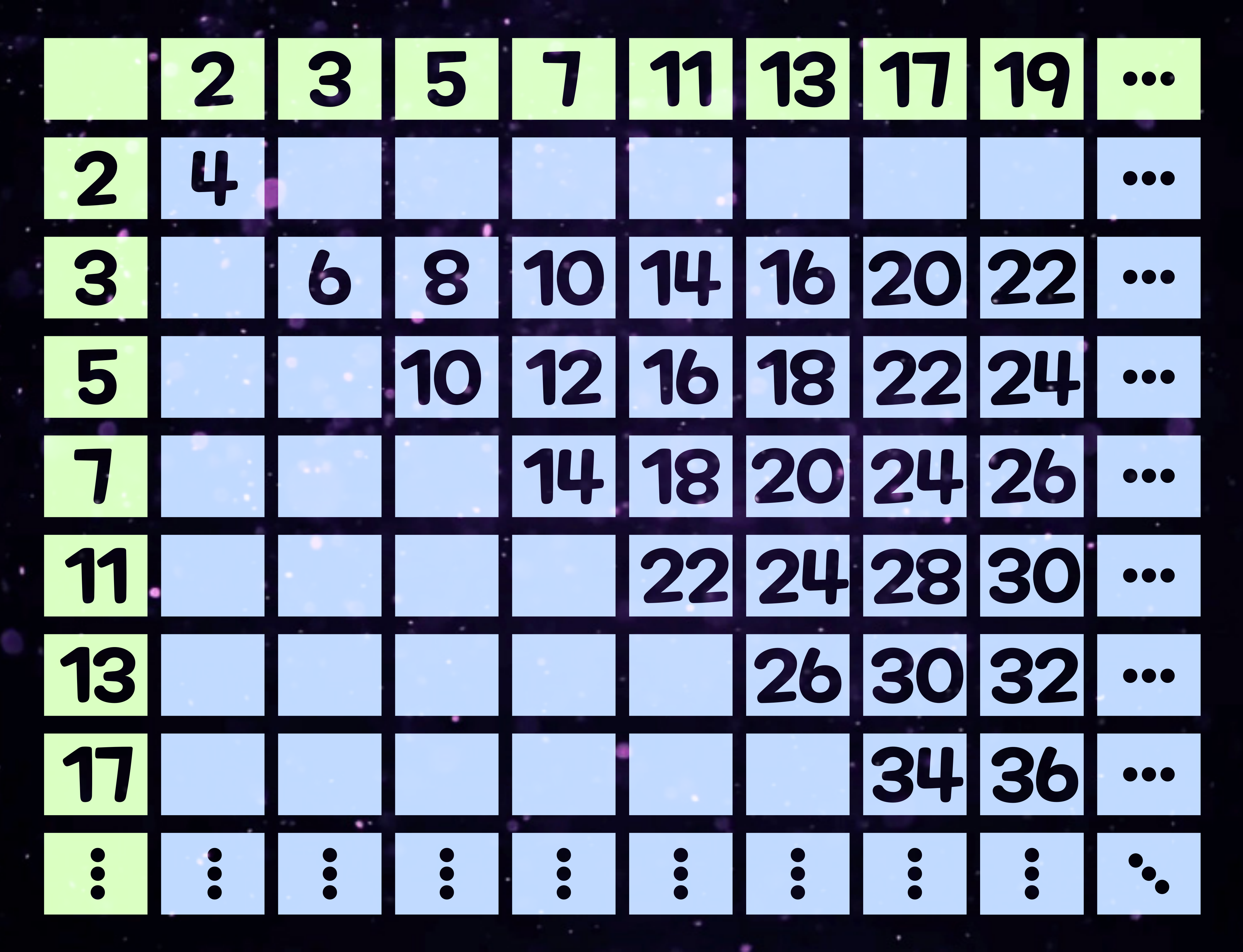
골드바흐의 추측을 작은 짝수로 확인해 보자. 아래의 표에서는 2개의 소수를 더해 얻어지는 수를 나타냈다. 가장 위의 가로행과 가장 왼쪽의 세로열에는 소수가 나열되어 있다. 표의 행과 열이 만나는 곳에는 각각의 소수를 더한 수를 적었다. 예컨대 5와 11이 만나는 곳은 16이고, 7과 17이 만나는 곳은 24이다. 2개 소수의 덧셈으로 4 이상의 짝수를 나타내고 있는 이 표를 보면, 36까지의 짝수가 모두 등장한다. 그러면 이 표를 넓혀서, 더하는 소수를 무한히 했을 때 표에 등장하지 않는 짝수가 있을까? 현재는 컴퓨터를 이용해 12억의 10배까지의 모든 짝수에 대해 추측이 성립한다는 사실이 확인되어 있다. 그러나 그 후의 짝수에 대해서도 정확히 성립하는지는 아직 아무도 모른다.
7-3. 리만 가설
'레온하르트 오일러(Leonhard Euler, 1707~1783)'소수 연구의 진전에 큰 공헌을 한 수학자이다. '레온하르트 오일러(Leonhard Euler)'는 '모든 자연수를 2제곱해 그 역수를 무한히 더해 나가면 몇이 될까?'라는, 당시 해결되지 않았던 문제를 연구했다. 역수란 2라면 2분의 1, 5라면 5분의 1과 같은 그 수를 분자로 한 수를 말한다. 그리고 오일러는 그 연구를 한 결과 다음과 같은 발견을 했다. 즉, 무한의 덧셈 식을 변형하면, 모든 소수를 나타내는는 무한의 곱셈이 된다는 것이다. (아래의 식 1)
그리고 오일러는 이 관계식을 더욱 발전시킨 식을 연구했다. 그 식은 바로 '제타 함수(Zeta Function)''라는 것이다. '제타 함수(Zeta Function)'는 오일러가 연구했던 식의 2제곱 부분을 2 이외의 수를 대입할 수 있는 식이다. 음수, 허수 등의 다양한 수가 대입 가능하다. '리만 가설(Riemann hypothesis)'은 수학에서 가장 어려운 문제라고도 평가받고 있다. (아래의 식 2)
