'M-이론'의 탄생

과학(Science)/물리학 (Physics)

'M-이론'의 탄생

SURPRISER - Tistory 2022. 8. 13. 11:43

지난 오랜 세월 동안 물리학자들은 '초공간(Hyperspace)'이란 개념을 신비주의자나 허풍 떨기 좋아하는 사람들의 전유물 정도로 취급했다. 눈에 보이지 않는 세계 '초공간'을 연구하는 과학자들은 학계의 조롱거리가 되기 일쑤였다. 하지만 '끈이론(String Theory)'과 'M-이론(끈이론의 최신버전 이론)'이 등장하면서 상황이 완전히 달라졌다. '일반 상대성 이론(General Theory of Relativity)'과 '양자역학(Quantum Mechanics)' 사이에 심각한 충돌이 야기되면서, 3차원 이상의 공간이 해결사로 등장했기 때문이다.

지금 전 세계의 이론물리학자들은 머리에 떠올리기조차 어려운 고차원 공간에서 상상의 나래를 펼치고 있다. 가장 근본적인 단계에서 우주에 관한 모든 지식은 '일반 상대성 이론'과 '양자역학'에 담겨 있다고 해도 과언이 아니다. 최근 들어 'M-이론(M-Theory)'이 각광을 받는 이유는 이 두 이론 사이의 충돌을 무마시켜서 '모든 것의 이론(ToE: Theory of Everything)'을 창출해낼 가장 강력한 후보로 대두되고 있기 때문이다. 지금까지 제시된 모든 이론들 중에서 아인슈타인이 말한 대로 '신의 마음을 읽을 수 있는 가능성'을 가진 이론은 'M-이론'뿐이다. 자연에 존재하는 모든 힘들을 하나의 우아한 이론체계로 통일하려면 10차원 또는 11차원의 '초공간(Hyperspace)'이 도입되어야 한다. 언뜻 듣기에 황당한 소리 같겠지만, 'M-이론(M-theory)'은 다음과 같은 의문에 대한 해답을 제시할 수 있는 유일한 후보이다. 우주가 태어나기 전에는 무엇이 있었을까? 시간은 거꾸로 흐를 수 있을까? 우리를 우주 저편으로 데려다줄 차원 입구는 과연 존재할까?

0. 목차

'통일장 이론'을 향하여
'끈이론'의 탄생
10차원
양자역학과 중력 사이에서 야기되는 수학적 모순
떠오르는 끈이론
끈이론이 주장하는 바
초공간의 문제점
왜 하필 끈이론인가?
끈이론이 직면한 문제
M-이론(M-Theory)

1. '통일장 이론'을 향하여

20세기부터 물리학자들은 우주의 모든 것을 하나의 통일된 논리로 설명하기 위해 필사의 노력을 기울여왔지만, 성공적인 이론은 단 하나도 없었다. 아인슈타인을 비롯한 세계의 천재들이 모두 실패한 이유는 무엇이었을까? 그것은 우주의 특성을 물리적으로 설명하려면 '일반 상대성 이론'과 '양자역학'이 반드시 고려되어야 하는데, 이 두 개의 이론은 적용 분야가 전혀 다르기 때문이다. '일반 상대성 이론'은 '블랙홀(Black Hole)', '빅뱅(Big Bang)', '퀘이사(Quasar)', '팽창하는 우주' 등 거시적인 규모에 적용되는 이론으로서, '트램펄린(Trampolin)' 막처럼 부드럽게 휘어진 대상을 다루는 구면 기하학에 기초를 두고 있다. 그러나 '양자역학'의 적용 분야는 '원자(Atom)', '양성자(Proton)', 중성자(Neutron)', '쿼크(Quark)' 등 지극히 작은 세계에 적용되는 물리학으로서 '양자(Quantum)'라는 작은 에너지 덩어리에 기초하고 있다. '상대성 이론'과는 달리 '양자역학'은 어떤 물리적 사건이 일어날 '확률(Probability)'만을 계산할 수 있기 때문에, 전자와 같은 입자들의 위치를 정확하게 알 수는 없다. 이 두 개의 이론은 '서로 다른 수학', '서로 다른 가정', '다른 원리'에 기초하고 있으며, 적용분야도 판이하게 다르다. 그렇기 때문에 이들을 통합하려는 모든 시도가 실패로 끝난 것은 그다지 놀라운 일이 아니다.

'에르빈 슈뢰딩거(Erwin Schrodinger)'와 '베르너 하이젠베르크(Werner Heisenberg)', '볼프강 파울리(Wolfgang Pauli)', '아서 에딩턴(Arthur Eddington)'을 비롯한 물리학자들은 '아인슈타인'의 뒤를 이어 물리법칙을 하나로 통일하려는 작업에 전념하였지만, 아무도 성공해내지 못했다. 1928년에 아인슈타인이 '통일장이론(Unified Field Theory)'의 초기 버전을 발표한 적이 있는데, 그 논문의 일부가 '뉴욕타임스(The New York Times)'에 실리면서 수백 명의 기자들이 그의 집 앞에 몰려들었다. 심지어 '아서 에딩턴'은 영국에서 이런 전보를 보내왔다. "지금 런던에서 가장 큰 백화점의 쇼윈도에도 당신의 논문이 붙어 있습니다. 지나가는 사람들이 발길을 멈추고 벌떼처럼 모여들어 당신의 세기적인 논문을 열심히 읽고 있습니다."

많은 물리학자들은 그 내용이 아무리 터무니없고 황당하다고 해도, '우주의 모든 것'을 커버하는 단순하고 우아한 '모든 것의 이론(ToE: Theory of Everything)'이 반드시 존재한다고 믿고 있다. 그러면 물리학자들이 '모든 것의 이론(ToE)'이 존재한다고 믿는 이유는 무엇일까? 프린스턴 고등과학원의 '존 휠러(John Wheeler, 1911~2008)'는 이런 말을 한 적이 있다. "19세기 사람들은 지구에 살고 있는 수많은 생명체들을 하나의 이론으로 설명하는 것이 불가능하다고 생각했다. 그러나 '로버트 찰스 다윈(Charles Robert Darwin, 1809~1882)'은 '자연선택(Natural Selection)'에 기초한 진화론을 도입하여 그 다양한 생명체들의 기원을 성공적으로 설명할 수 있었다.

1-1. '통일장 이론'을 완성했다고 주장했다가 망신을 당한 물리학자들

에르빈 슈뢰딩거(Erwin Schrodinger): 1946년에 '에르빈 슈뢰딩거'도 자신이 통일장이론을 완성했다면서, 급하게 기자회견을 요청한 적이 있었다. 물론 요즘은 자주 있는 일이지만, 그 무렵에 학자가 기자회견을 소집하는 것은 극히 이례적인 일이었다. 심지어 당시 아일랜드의 수상이었던 '이몬 드 벌레라(Eamon De Valera)'는 자세한 내용을 듣기 위해 '에르빈 슈뢰딩거'를 직접 찾아오기도 했다. '이몬 드 벌레라'가 '슈뢰딩거'에게 자세한 설명을 부탁하자, 다음과 같이 대답했다. "저는 이 이론이 옳다고 생각합니다. 틀린 것으로 판명된다면 국제적인 바보가 되겠지요." '뉴욕타임스(The New York Times)'의 기자들은 슈뢰딩거의 기자회견 내용을 정리하여 아인슈타인을 비롯한 몇몇 물리학자들에게 보내면서, 이론의 진위 여부에 대한 자문을 구했다. 그러나 아인슈타인은 자신이 연구 초기에 발견한 내용을 슈뢰딩거가 재발견한 것에 지나지 않는다며 공개적인 평을 거절했다. 아인슈타인은 자신의 견해를 솔직하게 밝힌 것뿐이었지만, 슈뢰딩거는 이 소식을 듣고 자존심이 크게 상했다.
'볼프강 파울리(Wolfgang Pauli)'와 '베르너 하이젠베르크(Werner Heisenberg)': 1958년에 컬럼비아대학에서 개최된 학회에서는 '볼프강 파울리(Wolfgang Pauli)'가 '베르너 하이젠베르크(Werner Heisenberg)'와 함께 개발한 '통일장이론'을 개발하고 있었다. 그러나 청중석에 안장 있던 '닐스 보어'는 '볼프강 파울리'의 이론에 회의적인 반응을 보이다가, 마침내 자리에서 벌떡 일어나 이렇게 외쳤다. "지금 우리는 당신이 제정신이 아니라는 점에 모두 동의하고 있소. 단지, 정신이 얼마나 심하게 나갔는지에 대해서 약간의 의견 차이가 있을 뿐이오!" '볼프강 파울리'는 '닐스 보어'가 하는 말의 의미를 금방 알아차렸다. '볼프강 파울리'와 '베르너 하이젠베르크'의 이론은 너무 상투적이고 평범하여 결코 통일장이론이 될 수 없다는 뜻이었다. 신의 마음을 읽으려면 새로운 수학과 파격적인 아이디어가 절실하게 요구되었던 것이다.

2. '끈이론'의 탄생

'끈이론(String Theory)'과 'M-이론(끈이론의 최신 버전 이론)'은 완전히 미쳐 돌아가는 듯하면서도 '통일장 이론'의 가장 유력한 후보로 꼽히고 있다. 특히 끈이론은 아주 특이한 역사를 가지고 있다. 원래 끈이론은 아주 우연히 발견되어 잘못된 분야에 적용되었다가 폐기처분되었다가, 어느 날 갑자기 '모든 것의 이론(ToE)'으로 화려하게 부활했다. 이 이론은 약간의 조절이 전체를 와해시킬 정도로 수학적 구조가 치밀하기 때문에 '모든 것의 이론(Theory of Everything)'이거나, 아니면 '아무것도 아닌 이론(Theory of Nothing)'이거나, 둘 중 하나이다.

끈이론은 매우 특이한 역사를 가지고 있다. 그렇게 된 이유를 한 마디로 말하면, '끈이론'은 거꾸로 진화한 이론이기 때문이다. 일반적으로 '상대성 이론'과 같이 일반적인 이론들은 기본적인 원리에서 출발하여, 일련의 방정식을 유도하는 식으로 진화하는 것이 일반적이다. 그 후, 방정식으로부터 '양자적 요동(Quantum Fluctuation)'이 성공적으로 계산되면 정식으로 인정받는 이론으로 등극하게 되는 것이다. 그러나 끈이론은 이 과정을 완전히 거꾸로 밟아왔다. 즉, 끈의 양자 이론이 제일 먼저 발견되어 지금에 이르고 있는 것이다. 그래서 물리학자들은 '끈이론'의 원리가 무엇인지 알아내기 위해 지금도 고민을 하고 있다.

2-1. 끈이론의 기원

끈이론의 기원은 1968년까지 거슬러 올라간다. 당시 두 젊은 물리학자 '가브리엘레 베네치아노(Gabriele Veneziano)'와 '미히코 스즈키(Mahiko Suzuki)'는 18세기의 천재 수학자 '레온하르트 오일(Leonhard Euler)'이 발견한 '오일러 베타 함수(Euler Beta Function)'와 씨름을 벌이던 중, 이 함수가 원자 세계의 물리학을 신기할 정도로 정확하게 서술하고 있다는 놀라운 사실을 발견했다. 두 개의 '파이중간자(π-meson)'가 충돌하면서 엄청난 에너지가 양산되는 물리적 과정이 추상적인 수학공식과 너무도 정확하게 일치했던 것이다. 그 후 '가브리엘레 베네치아노'의 모형은 물리학계에 일대 센세이션을 일으키면서 그의 아이디어를 '강력(원자핵을 이루는 핵자 사이에 작용하는 힘)'에 적용하는 수백 편의 논문들이 줄줄이 발표되었다.

사실 끈이론은 아주 우연히 발견된 이론이다. 끈이론이 처음 탄생하던 당시만 해도, 물리학은 자연을 주의 깊게 관측한 후 몇 가지 가정하에 관측자료를 끈질기게 반복 검증하면서 형성되어 왔다. 그러나 끈이론은 아무런 계획도 없이 오로지 해답을 추측해가면서 만들어진 이론이다. 당시만 해도 이런 식의 '지름길 물리학'이 가능하리라고 생각했던 사람은 거의 없었다.

2-2. '강력의 산란 행렬'과 '오일러 베타함수'가 일치한다는 사실을 발견했다.

원자 세계의 입자들은 크기가 너무 작아서 성능이 가장 뛰어난 기구를 사용한다 해도 눈으로 직접 볼 수는 없다. 그래서 물리학자들은 엄청난 에너지로 이들을 두드렸을 때 나타나는 현상을 관측함으로써 소립자의 특성을 간접적으로 추정해왔다. 이때 사용하는 기구가 바로 '입자가속기(Particle Accelerator)'이다. '입자가속기'는 소립자를 빠른 속도로 가속시켜서 표적과 충돌시켜 원자의 내부 구조를 관측하는 장비로서, 큰 것은 직경이 수 km에 이른다. 물리학자들은 이 장비를 이용해 초대형 충돌을 일으킨 후, 거기서 튀어나오는 파편을 분석함으로써 원자의 내부구조를 간접적으로 연구하고 있다. 이 실험의 최종 목적은 '산란 행렬(Scattering Matrix 또는 S-matrix)'을 이루는 일련의 숫자들을 알아내는 것이었다. '아원자(원자를 구성하는 입자)'세계의 모든 정보들은 이 숫자에 들어 있기 때문에, 일단 '산란 행렬(S-matrix)'이 알려지기만 하면 소립자의 모든 특성을 유추할 수 있게 된다.

'입자물리학(Particle Physics)'이 추구하는 목표 중 하나는 강력에 관한 '산란 행렬'의 수학적인 구조를 예측하는 것이다. 그러나 그 과정이 너무 어렵고 복잡하여 과거의 물리학자들은 '현재의 물리학 수준으로는 이룰 수 없는 목표'라고 생각했었다. 그런데 '가브리엘레 베네치아노(Gabriele Veneziano)'와 '미히코 스즈키(Mahiko Suzuki)'가 오래된 수학책을 뒤지다가 '강력의 산란 행렬'과 '오일러 베타 함수'가 일치한다는 사실을 발견한 것이다.

다만 '베네치아노'와 '스즈키'가 제안한 모형은 몇 가지 문제점을 가지고 있었다. 그중 하나는 '오일러 베타 함수'가 '산란 행렬'의 정확한 값이 아닌 '1차 근사값'에 해당한다는 점이었다. 위스콘신대학의 '분지 사키타(Bunji Sakita)'와 '미구엘 비라소로(Miguel Virasoro)' 그리고 '케이지 키카와(Keiji Kikawa)'는 '산란 행렬(Scattering Matrix)'이 무한급수의 형태로 표현될 수 있으며, 베네치아노의 모형은 이중 가장 중요한 첫 번째 항에 해당한다는 사실을 알아냈다.

2-3. 제안된 모형은 어떠한 수정도 허용되지 않았다.

이들이 제시한 모양은 전례를 찾아볼 수 없을 정도로 독특한 것이었다. 일반적으로 누군가가 새로운 이론을 제기하면, 그 이론에 포함되어 있는 간단한 변수들을 이리저리 바꾸면서 진위 여부를 검증한다. 그러나 '가브리엘레 베네치아노(Gabriele Veneziano)'와 '미히코 스즈키(Mahiko Suzuki)'가 제시한 모형은 처음부터 너무 완벽하게 짜여 있어서, 변수를 조금만 바꿔도 이론 전체가 와해될 지경이었다. 그것은 마치 완벽하게 세공된 보석처럼, 어떠한 형태의 변형도 허용하지 않는 희한한 이론이었다.

물리학자들은 '베네치아노'가 제안했던 모형의 변수들을 변형시켜 수백 편의 논문을 발표했지만, 지금까지 살아남은 이론은 단 하나도 없다. 살아남은 논문들은 '변수를 수정한 것'이 아니라, 베네치아노와 스즈키가 제안한 모형이 '현실과 일치하지 않는 이유'를 추적한 논문들이다. 즉, 이론이 보유하고 있는 대칭성을 분석한 논문만이 오늘날까지 그 생명력을 유지하고 있다. 결국, 물리학자들은 '베네치아노'와 '스즈키'가 제안한 모형이 어떠한 수정도 허용되지 않는다는 것을 인정할 수밖에 없었다.

2-4. 초끈이론의 탄생

마침내 시카고대학의 '요이치로 남부(Yoichiro Nambu)'와 니혼대학의 '데쓰오 고토(Tetsuo Goto)'가'베네치아노'와 '스즈키'가 제안한 모형의 비밀을 풀었다. 그것은 바로 진동하는 끈의 수학적 표현이었던 것이다. 두 개의 끈이 서로 충돌했을 때 나타나는 산란 행렬은 '베네치아노'와 '스즈키'가 제안한 모형으로 서술되는데, 이때 개개의 입자들은 '점(Point)'가 아니라 진동하는 '끈(String)'으로 간주할 수 있다.

그 후로 상황은 빠르게 변해갔다. 1971년에 '존 슈바르츠(John Schwarz, 1941~)', '앙드레 느뵈(André Neveu, 1946~)', '피에르 라몽(Pierre Ramond, 1943~)'은 끈 모형에 '스핀(Spin)'을 도입하여, 입자들 간의 상호작용을 끈이론을 서술할 수 있는 기초를 마련했다. 모든 입자들은 팽이처럼 자전에 해당하는 '스핀 값'을 가지고 있다. 각 입자의 스핀은 양자 단위로 0, 1, 2, 3...과 같은 정수이거나 1/2, 3/2...와 같이 반정수인 경우가 있는데, 느뵈-슈바르츠-라몽이 예견한 끈의 스핀도 이와 동일한 분류를 보이고 있다.

2-5. 소립자들은 '점입자'가 아니라 '단 하나의 진동하는 끈'

전통적으로 입자물리학자들은 '전자(Electron)'를 무한히 작은 '점입자(Point Particle)'로 간주해 왔다. 이 관점을 유지한 채 그 많은 소립자의 존재를 설명하려면, 수백 가지의 점입자들을 새로 도입해야 하는데, 이것은 누가 봐도 번거로울 뿐만 아니라, 이론 자체도 복잡해질 것이 분명하다. 하지만 초끈이론을 도입하면 이 난처한 상황이 말끔하게 정리된다. 만약 누군가가 초강력 현미경을 개발되어 소립자 규모의 세계를 볼 수 있게 된다면, 우리의 눈에 보이는 것은 수백 가지의 점입자가 아니라 단 하나의 '진동하는 끈'뿐일 것이다. 우리가 소립자들을 하나의 점처럼 생각하는 이유는 그들이 진짜 점이기 때문이 아니라, 그것을 관측하는 기구가 너무 미개하기 때문이다.

이 작은 끈들은 각기 다른 진동수와 다른 패턴으로 끊임없이 진동하고 있다. 만약 이들 중 하나를 골라서 기타 줄을 튕기듯이 쥐어뜯는다면, 끈의 진동 패턴이 바뀌면서 다른 입자로 변환될 것이다. 그리고 끈을 또 한차례 쥐어뜯으면 또 다른 입자로 바뀔 것이다. 이처럼 초끈이론에서는 자연에 존재하는 모든 입자들을 각기 '다른 형태로 진동하는 끈'으로 간주하고 있다. 이렇게 생각하면 우리는 많은 입자들을 일일이 상대가 필요가 없기 때문에, 통일된 이론체계를 세우는데 매우 유리해진다. 이 논리에 의하면, 인류가 지금까지 밝혀낸 물리학의 모든 법칙들은 '끈(String)'과 '막(Membrane)'의 조화 법칙으로 요약될 수 있다.

2-6. 끈의 장이론

영국의 물리학자 '마이클 패러데이(Michael Faraday)'가 '장(Field)'의 개념을 도입한 후로 지난 150년 동안 물리적 장에 기초하여 모든 것을 이해하고 있었다. 예컨대, 막대자석의 주변에 형성되는 '자기력선(자기장의 선)'을 생각해 보자. 이 선은 거미줄처럼 전 공간에 퍼져 있으며, 우리는 각 지점마다 자기장의 세기와 방향을 계산할 수 있다. 일반적으로 '장(Field)'이란 공간의 모든 지점에서 각기 다른 값을 갖는 수학적 객체를 통칭하는 용어이다. 따라서 장은 우주 내의 모든 지점에서 자기력, 전기력, 핵력 등의 크기와 방향에 관한 정보를 담고 있다. 바로 이런 이유 때문에 전기, 자기, 핵력, 중력을 가장 근본적인 단계에서 서술할 때 장의 개념이 도입되어왔던 것이다. 그렇다면 '끈(String)'이라고 해서 '장(Field)'의 개념이 도입되지 않을 이유는 없지 않을까? 물리학자 '미치오 카쿠'는 이 문제에 도전하기로 마음먹고 오사카대학에 있는 '케이지 키카와(Keiji Kikawa)'와 함께 '끈의 장이론'을 유추해 내는 데 성공했다. 이들은 끈이론에 담겨 있는 모든 정보들을 약 엄지손가락만한 길이의 방정식에 함축시킬 수 있었다.

'끈의 장이론'을 완성시킨 후, 물리학자 '미치오 카쿠'는 물리학계의 학자들을 일일이 만나서 구축한 이론의 잠재력과 아름다움을 설득시켜야 했다. 그해 여름에 '미치오 카쿠'는 콜로라도의 '애스펀 센터(Aspen Center)'에서 개최된 물리학회에 참석하여 소수의 선별된 물리학자들 앞에서 이론을 소개하였다. 당시 좌중에는 두 명의 노벨상 수상자인 '머리 겔만(Murray Gell-Mann)'과 '리처드 파인만(Richard Feynman)'이 함께하고 있었는데, 이들은 날카롭고 신랄한 질문을 퍼부어 발표자를 당혹스럽게 만드는 것으로 유명한 사람들이었다. '미치오 카쿠'는 강연을 진행하면서, 끈의 장이론을 도입하면 방정식들이 뒤죽박죽으로 엉켜 있는 끈이론을 가장 단순하고 포괄적인 형태로 정리할 수 있다고 강조하였다. '끈의 장이론'을 도입하면 '가브리엘레 베네치아노(Gabriele Veneziano)'와 '미히코 스즈키(Mahiko Suzuki)'가 제시한 모형과 '건드림 근사법(Perturbation Approximation)'의 무한히 많은 항들, 그리고 끈의 모든 특성들을 엄지 손가락만한 길이의 방정식으로부터 유추해낼 수 있다. '미치오 카쿠'는 끈이론의 대칭성이 수학적인 아름다움과 함께, 막강한 위력을 갖고 있다는 점을 강조하였다. 강연이 끝나고 위대한 물리학자 '리처드 파인만(Richard Feynman)'은 "저는 끈이론에 완전히 동조하는 입장은 아닙니다만, 당신의 강연은 제가 지금까지 들었던 강연들 중에서 단연 최고였습니다."라는 말을 남겼다.

3. 10차원

3-1. 초끈이론은 10차원의 시공간에서만 성립했다.

그러나 끈이론은 탄생하자마자 곧바로 심각한 문제에 부딪혔다. '뉴저지 주립대학교(The State University of New Jersey)'의 '클로드 러블레이스(Claude Lovelace)'가 다음과 같은 사실을 발견했기 때문이다. 그는 '베네치아노'와 '스즈키'의 모형에는 조그만 수학적 결함이 있는데, 이 문제가 해결되려면 끈이 살고 있는 '시공간(Time-space)'은 26차원이어야 한다. 또한 느뵈-슈바르츠-라몽이 제안했던 '초끈이론(Superstring theory)'에서는 시공간이 10차원이어야 했다.

이 사실이 알려지면서 물리학자들은 엄청난 충격에 휩싸였다. 과학 역사상 이토록 황당한 주장이 또 있었을까? 혁신적인 이론을 만들었던 뉴턴과 아인슈타인은 다른 차원에서 이론을 전개해나갈 수도 있었지만 '3차원 공간+1차원 시간'의 영역을 결코 벗어나지 않았다. 예를 들어, 거리의 제곱에 반비례한다는 중력 법칙은 4차원 공간으로 확장하여 거리의 세제곱에 반비례하는 '4차원 중력이론'으로 대치될 수 있다. 그러나 끈이론은 '차원을 확장할 수도 있다.'가 아니라, '확장된 차원에서만 성립한다.'는 황당한 이론이었다.

현실적으로 봤을 때, 이것은 일대 재앙이 아닐 수 없다. 우리가 속한 우주는 아무리 눈을 씻고 봐도 3차원의 공간과 1차원의 시간으로 이루어져 있음이 분명하다. 이것을 10차원으로 확장한다는 것은 과학을 공상과학소설의 영역으로 확장하는 것이나 다름없다. 그래서 초기의 끈이론 학자들은 종종 비웃음의 대상이 되곤 했다. '리처드 파인만'과 '존 슈바르츠'가 엘리베이터를 타고 있을 때, 파인만이 "하이 존! 오늘은 몇 차원에서 살고 계신가?"라는 농담을 건넨 적도 있다고 한다. 그들은 이론의 단점을 극복하기 위해 필사적으로 노력했지만, 만족스러운 결과를 얻지 못하고 대부분 연구를 그만두었다. 오직 끈이론을 자신의 목숨처럼 여기는 고집불통 학자들만이 근근히 명목을 유지해 나갈 뿐이었다.

3-2. 끈이론은 '모든 것의 이론'이었다.

이 암울했던 시기에 끝까지 끈이론을 고집했던 두 명의 물리학자가 있었다. '칼텍(캘리포니아 공과대학교)'의 '존 슈바르츠(John Schwarz)'와 파리 고등 사범학교의 '조엘 셔크(Joël Scherk, 1946~1980)'가 바로 그들이었다. 그때까지만 해도 끈이론은 '핵력(원자핵을 이루는 핵자 사이에 작용하는 힘)'을 설명하는 이론으로 알려져 있었는데, 거기에는 한 가지 문제점이 있었다. 강력과 무관하고 '질량이 0이고 스핀이 2인 입자'가 끈이론에 포함되어 있었던 것이다. 학자들은 이 성가신 입자를 어떻게든 없애보려고 백방으로 노력했지만, 모두 헛수고로 끝났다. 스핀 2인 입자를 없애기만 하면 이론 전체가 와해되면서 신비한 능력을 상실해버리곤 했다. 아무래도 이 입자가 이론에 숨어 있는 비밀의 근원인 것 같았다.

'존 슈바르츠'와 '조엘 셔크'는 이 문제를 해결하기 위해 대담한 추론을 세웠다. 질량이 0이고 스핀이 2인 성가신 입자를 '중력자(중력을 매개하는 입자)'로 간주하자, 아인슈타인의 '중력 이론'과 '끈이론'이 조화롭게 합병되었다. 다른 양자이론들은 가능하면 중력자를 이론에 포함시키지 않으려고 애를 썼던 반면에, 끈이론은 '중력자'를 전면에 내세우고 중력과의 화해를 시도하였다. (오히려 중력을 포함시키지 않으면, 이론 자체가 맞아 들어가지 않는다는 점이 끈이론의 커다란 장점으로 작용하였다.)

이리하여 과학자들은 그동안 끈이론이 엉뚱한 분야에 적용되어왔다는 사실을 깨닫게 되었다. 그것은 핵력만을 위한 이론이 아니라 자연의 모든 것을 서술하는 '모든 것의 이론(Theory of Everything)'이었던 것이다. '에드워드 위튼(Edward Witten, 1951~)'이 강조한 바와 같이, 끈이론의 커다란 매력 중 하나는 이론체계 안에 중력이 포함되어 있다는 점이다. '표준 장이론'은 '중력(Gravity)'를 설명하는 데 실패했지만, 끈이론에서 중력은 필수 불가분의 요소였다. 그러나 대부분의 물리학자들은 '존 슈바르츠'와 '조엘 셔크'의 아이디어를 수용하지 않았다. 끈이론이 중력과 원자 세계에 모두 적용되려면 끈의 길이는 '10^-33cm(플랑크길이)'를 넘지 않아야 하는데, 이것은 양성자 크기의 (10억×10억 분)의 1에 불과했으므로 입자를 서술하기에는 너무 작다고 생각했던 것이다.

4. 양자역학과 중력 사이에서 야기되는 수학적 모순

통일장이론을 완성하려는 다양한 시도는 1980년대 중반까지 계속되었다. 그러나 표준모형에 중력을 끼워 넣기만 하면 예외 없이 '무한대'라는 괴물이 등장하여 애써 구축한 이론을 사지로 몰아넣었다. 양자역학과 중력을 연결시키려는 모든 시도는 수학적인 모순을 낳으면서 이론 자체를 붕괴시켰다. 양자역학과 중력 사이에 야기되는 수학적 모순은 크게 두 가지로 분류될 수 있다.

무한대 문제: 첫 번째는 무한대에 관한 문제이다. 일반적으로 '양자적 요동'은 지극히 작은 영역에서 미세한 강도로 발생한다. 양자적 효과는 뉴턴의 법칙에 아주 작은 수정을 가할 뿐이다. 그래서 우리에게 친숙한 거시 세계에서는 양자역학에 의한 효과를 아예 무시하고 살아도 별 탈이 없는 것이다. 그러나 양자역학에 중력이 개입되면, 양자적 요동이 무한대로 커지면서, 더 이상의 논리를 전개할 수가 없게 된다.
'비정상성(Anomaly)' 문제: 두 번째는 '양자적 요동'을 이론에 첨가했을 때, 이론이 정상에서 이탈하는 정도, 즉 '비정상성(Anomaly)'에 관한 문제이다. 즉, 이론이 보유하고 있는 대칭성이 '비정상성'에 의해 붕괴되면서 위력을 상실하게 되는 것이다.

물리학자들은 '중력'과 양자이론'을 결혼시키기 위해 20세기부터 지금까지 노력해왔으나, 그때마다 나타나는 '무한대'와 '비정상성(Anomaly)'에 막혀 뜻을 이루지 못했다. 그러는 동안 학계에서는 임시변통을 포기하고, 완전히 다른 기초에서 새롭게 시작해야 한다는 의견이 서서히 대두되기 시작했다.

5. 떠오르는 끈이론

5-1. 끈이론에 존재하던 불일치가 해결되면서, 끈이론이 급부상하였다.

1984년에 칼텍의 '존 슈바르츠(John Schwarz)'와 런던 '퀸 메리 대학(Queen Mary's College)'의 '마이크 그린(Mike Green, 1946~)'은 끈이론에 존재하는 불일치를 해결하면서, 끈이론은 극적인 전환기를 맞이하게 된다. 당시 물리학자들은 끈이론에 수학적 무한대가 존재하지 않는다는 것을 이미 알고 있었다. 그러나 '존 슈바르츠'와 '마이크 그린'은 심각한 문제를 야기했던 '비정상성(Anomaly)'까지 말끔하게 제거했고, 그 후로 끈이론은 '모든 것의 이론(ToE: Theory of Everything)'을 구현할 가장 강력한 후보로 급부상하게 되었다.

불과 얼마 전까지만 해도 '이미 죽은 이론'으로 치부되었던 끈이론은 이 사건으로 인해 극적인 부활을 맞이하였다. '아무것도 아닌 이론(Theory of Nothing)'에서 하루 아침에 '모든 것의 이론(Theory of Everything)'으로 그 평가가 달라진 것이다. 물리학자들은 앞다투어 끈이론과 관련된 논문을 읽기 시작했고, 전 세계의 연구소에서 끈이론을 다룬 논문들이 쏟아져 나왔다. 그리고 황당무계한 공상과학소설쯤으로 치부되던 '평행우주(Parallel Universe)'도 물리학의 주요 이슈로 떠오르기 시작했다. 끈이론을 향한 열풍은 정말 대단했다.

1991년 8월에 발행된 '디스커버(Discover)'의 표지에는 다음과 같은 제목이 실렸다. "새롭게 등장한 모든 것의 이론: 한 물리학자가 우주의 궁극적이 수수께끼에 도전장을 던지다." 이 기사에는 명예를 추구하는 한 물리학자의 말이 다음과 같이 인용되어 있었다. "저는 결코 겸손한 사람이 아니며, 그런 사람이 되고 싶지도 않습니다. 만일 제가 끈이론으로 성공을 거둔다면 노벨상은 당연히 저에게 주어질 것입니다." 또한 그는 끈이론이 아직 불완전하다고 주장하는 사람들을 향해 다음과 같이 포문을 열었다. "끈이론에 반대하는 사람들은 이론의 진위 여부가 증명되려면 적어도 400년 이상을 기다려야 한다고 주장하고 있는데, 저는 그들에게 이런 말을 해주고 싶습니다. '입 다물고 지켜보기나 해라!"

5-2. 끈이론을 반대하는 사람들

하지만 동시에 끈이론을 반대하는 사람들도 많았다. 하버드대학의 물리학자 중 한 사람은 '끈이론은 물리학이 아니라 수학이나 철학에 가까운 이론이다.'라고 반박했고, 노벨상 수상자인 '셸던 리 글래쇼(Sheldon Lee Glashaw, 1932~)'는 끈이론 추종자들을 검증할 수 없는 이론에 엄청난 예산을 소비한다는 의미에서 '스타워즈 프로그램'에 비유했다. '셸던 리 글래쇼'는 끈이론을 연구한다고 해서 반대론자들을 방해하는 것은 아니므로, 다수의 젊은 물리학자들이 끈이론에 관심을 보이는 것은 바람직한 현상이라고 말했다.

한편, '에드워드 위튼'은 '양자역학이 지난 50년 동안 물리학을 이끌어온 것처럼, 끈이론은 향후 50년 동안 물리학을 이끌어갈 것이다.'라고 했다. '셸던 리 글래쇼'는 하버드의 물리학자들이 끈이론을 연구하는 것을 원치 않았으나, 차세대의 물리학자들이 끈이론으로 몰려가는 대세를 바꾸기에는 역부족이었다. 실제로 그 후 하버드대학 물리학과는 끈이론을 연구하는 젊은 물리학자를 여러 명 채용하였다.

6. 끈이론이 주장하는 바

6-1. 소립자는 '점'이 아니라 진동하는 '끈'이다.

끈이론이 주장하는 바는 기본적으로 다음과 같다. 입자의 구체적인 형태를 보여주는 초고성능 현미경이 개발되어 이 기구로 소립자들을 들여다본다면, 우리의 눈에 보이는 것은 '점(point)'가 아니라 진동하는 '끈(String)'이라는 것이다. 만약 누군가가 이 끈을 퉁긴다면 진동 패턴이 달라지면서 입자의 종류가 달라질 것이다. 예컨대 '전자(Electron)'가 '중성미자(Neutrino)'로 바뀌는 식이다. 여기서 끈을 또 한 번 튕기면 '쿼크(Quark)'가 될 수도 있다. 실제로 끈을 충분히 세게 퉁길 수만 있다면, 현존하는 모든 입자들을 다 만들어 낼 수 있다. 끈이론은 자연계에 다양한 입자들이 존재하는 이유를 이런 식으로 설명하고 있다. 즉, 모든 입자들은 동일한 끈이 다양한 패턴으로 진동하면서 나타난 결과라는 것이다. 입자의 종류가 다양한 것은 끈의 진동 패턴이 그만큼 다양하기 때문이다. 그렇다면 끈은 얼마나 다양하게 진동할 수 있을까? 이것을 결정하는 것이 바로 물리학의 법칙이다.

6-2. 끈이론은 '양자역학'과 '일반상대성이론'을 모두 포함한다.

끈이론은 양자역학에 등장하는 입자들뿐만 아니라, 아인슈타인의 중력이론까지도 끈의 진동으로 설명하고 있다. 끈의 최저 진동상태, 즉 '질량=0이고 스핀=2에 해당하는 입자'는 중력의 매개입자인 '중력자(Graviton)'로 해석함으로써, 이론물리학의 오랜 숙원이었던 '중력의 양자화'를 실현한 것이다. 끈이론이 예견한 '중력자'를 대상으로 상호작용을 계산하면, 아인슈타인의 중력이론은 양자역학 버전으로 변환된다. 끈이 움직이고, 분리되고, 또는 변형되면서 시공간에 커다란 제약을 가하게 되는데, 이러한 제한조건으로부터 아인슈타인의 '일반 상대성 이론'을 유추해낼 수 있다. 다시 말해서, 끈이론 속에는 이미 '일반 상대성 이론'이 포함되어 있다는 것이다.

'에드워드 위튼(Edward Witten)'은 다음과 같이 말했다. "아인슈타인이 상대성이론을 발견하지 못했다고 하더라도, 그것은 끈이론의 부산물로 어차피 탄생할 이론이었다."

7. 초공간의 문제점

그러나 자연에 높은 차원의 공간이 정말로 존재한다면, 끈이론 학자들은 '시어도어 칼루자(Theodor Kaluza, 1885~1954)'와 '펠릭스 클라인(Felix Klein, 1849~1925)'이 최초로 고차원 이론을 연구하면서 마주쳤던 문제에 똑같이 똑같이 직면하게 된다. 높은 차원은 대체 어디에 숨어있단 말인가?

7-1. 아인슈타인 방정식을 확장하면, 자연에 존재하는 힘들이 하나씩 그 모습을 드러낸다.

무명의 수학자였던 '시어도어 칼루자(Theodor Kaluza)'는 아인슈타인 방정식을 '5차원(4차원 공간과 1차원 시간)'에서 재구성한 후, 아인슈타인에게 한 통의 편지를 보냈다. 사실 '아인슈타인 방정식'은 임의의 차원으로 쉽게 확장시킬 수 있었으므로, '시어도어 칼루자'의 아이디어는 전혀 새로운 것이 아니었다. 그러나 그가 보낸 편지에는 놀라운 내용이 적혀 있었다. 아인슈타인 방정식을 5차원으로 확장시킨 후 다섯 번째 차원에 해당되는 부분을 골라내서 보니, 놀랍게도 '맥스웰 방정식(Maxwell's equations)'과 일치하더라는 것이다. 다시 말해서, '제임스 맥스웰'의 '전자기이론(Electromagnetic Theory)'이 '5차원 아인슈타인 방정식'에 자동으로 포함되어 있다는 뜻이다. 우리는 다섯 번째 차원을 볼 수 없지만, 이곳에서 형성된 파동이 바로 '빛(Light)'에 해당된다는 이야기다. 이것은 정말 기쁜 소식이 아닐 수 없다. 지난 150년 동안 물리학자들과 공학자들은 복잡하기 그지없는 '맥스웰 방정식'을 외우기 위해 무진 고생을 해왔다. 그런데 이 방정식이 5차원으로 확장된 아인슈타인의 방정식이 일부였다는 것이다.

또 나중에 증명된 사실이지만, 아인슈타인 방정식의 차원을 더 확장하여 진동의 특성을 부여하면, 고차원 진동으로부터 'W-보존'과 'Z-보존', '글루온'이 자연스럽게 유도된다. 참고로 'W-보존(W-boson)'과 'Z-보존(Z-boson)'은 약력의 매개입자이고, '글루온(Gluon)'은 강력의 매개입자이다. '아인슈타인 방정식'을 출발점으로 삼아 차원을 계속 확장시켜나가면 자연에 존재하는 모든 힘들이 하나씩 그 모습을 드러낸다. '시어도어 칼루자'의 방식이 맞다면 자연은 우리가 생각했던 것보다 훨씬 단순한 구조를 갖고 있는 셈이다.

7-2. 고차원 아이디어의 문제점

아인슈타인은 '시어도어 칼루자((Theodor Kaluza)'의 편지를 받고 커다란 충격을 받았다. 모든 것이 거짓말처럼 잘 맞아 들어갔기 때문이다. 그러나 몇 년이 지난 후 칼루자의 아이디어에서 몇 가지 문제점이 발견되었다. 첫 번째 문제는 그의 이론이 '양자중력이론(양자역학과 중력이론을 합친 이론)'과 마찬가지로 '무한대'와 '비정상성'을 포함하고 있다는 점이었고, 두 번째 문제는 "우리는 왜 다섯 번째 차원을 볼 수 없는가?"였다.

하늘을 향해 쏘아 올린 화살은 결코 다른 차원 속으로 사라지지 않는다. 공간의 모든 지점으로 골고루 퍼지는 연기조차도 결코 사라지지 않는다. 그래서 물리학자들은 우리가 살고 있는 공간에 더 높은 차원이 존재한다면, 그것은 원자보다 작은 영역 속에 숨어 있어야 한다고 생각했다. 지난 한 세기 동안 수학자들이 고차원 아이디어에 몰두하고 있을 때, 물리학자들은 현실적인 증거가 없다며 그들을 비웃었다. 하지만 고차원 아이디어가 물리학의 중앙 무대에 등장하면서, 물리학자들은 고차원과 관련된 문제들을 더 이상 무시할 수 없게 되었다.

7-3. 높은 차원은 아주 작은 영역 속에 숨어 있다는 가정을 세웠다.

물리학자들은 칼루자의 아이디어를 구제하기 위해, 높은 차원이 아주 작은 영역 속에 숨어 있기 때문에 보이지 않는다는 가정을 내세웠다. 우리가 사는 세계는 공간과 시간을 합해 4차원이므로, 만약 다섯 번째 차원이 존재한다면, 원자보다 작은 영역 속에 원형으로 '돌돌 말려 있어서' 눈에 뜨이지 않는다고 생각하는 수밖에 없다.

끈이론도 이와 동일한 문제에 직면하였다. 초기의 끈이론이 주장했던 시공간은 10차원이었으므로, 우리가 알고 있는 4차원을 제외한 나머지 '여분 차원'들을 극미의 영역 속에 구겨 넣어야 했다. 이것을 '차원 다짐(Dimensional Compactification)'이라고 한다. 끈이론에 의하면, 이 우주는 원래 모든 힘들이 한 종류로 통합되어 있는 10차원의 객체였다. 그러나 10차원 초공간은 매우 불안정한 상태였으므로, 빅뱅이라는 거대한 사건을 겪으면서 여섯 개의 차원은 아주 작은 영역 속으로 말려들어가고 지금과 같이 4차원의 시공간만 남게 되었다는 것이다. 말려 들어간 6개의 차원은 너무나 작은 곳에 숨어있기 때문에 볼 수도 없고, 그 안에 어떤 다른 객체가 존재할 수도 없다.

예컨대, 정원에 물을 뿌릴 때 사용하는 호스를 멀리서 보면 길이만 있는 1차원 물체처럼 보이지만, 가까이 다가가서 보면 호스의 면은 1차원이 아니라 2차원 곡면임을 알 수 있다. 즉, 호스의 원형 단면을 따라 돌아가는 또 하나의 차원이 숨어 있는 것이다. 공간에 여분의 차원이 숨어있다는 가정도 이와 비슷한 맥락에서 이해할 수 있다.

8. 왜 하필 끈이론인가?

지난 세월 동안 끊임없이 제기되었던 다양한 '통일장이론(Unified field theory)'은 모두 사장되어지만, 끈이론은 끝까지 살아남았다. 지금은 끈이론을 대신할 만한 다른 이론은 전무한 상태이다. 그러면 끈이론은 어떻게 이토록 막강한 위력을 발휘할 수 있었을까? 양자역학과 중력 사이에서 야기되는 수학적 모순에는 '무한대 문제(infinity Problem)'와 '비정상성(Anomaly Problem)'이 있다고 하였다. 그러면 끈이론은 이 두 가지 문제를 어떻게 해결했을까? '끈'의 '위상'과 '초대칭'이 이 두 가지 문제를 해결해 준다.

8-1. 끈의 위상

크기를 가진 최소단위 '끈(String)'을 만물의 기본으로 삼으면, 점입자 이론에 수시로 나타나는 무한대 문제를 피해갈 수 있다. 뉴턴의 중력만 해도, 점입자를 향해 점차 가까이 접근하면 중력의 크기는 무한대로 발산한다. 뉴턴의 중력 거리의 제곱에 반비례 함으로, 거리가 0으로 접근하면 중력은 무한대가 된다. '양자역학(Quantum Mechanics)'에서도, 점입자에 가까이 접근하면 힘은 무한대로 발산한다. 지난 수십 년 동안 물리학자들은 이 문제를 해결하기 위해, 별의별 방법을 다 동원해왔다. '리처드 파인만'은 '재규격화(Renormalization)'라는 과정을 통해 무한대를 제거했고, 다른 물리학자들은 주로 무한대를 단지 옆으로 치워놓는 식으로 무한대 문제를 피해왔다. 그러나 양자중력이론에서는 '리처드 파인만'의 처방을 적용해도 무한대가 제거되지 않았다. 이 모든 것은 입자를 '크기가 없는 점'으로 간주했기 때문에 나타난 결과였다. 하지만 끈이론은 입자를 '점(Point)'이 아닌 '끈(String)'으로 간주하고 있으므로, 점입자에 의한 '무한대 문제'는 발생하지 않는다.

끈은 점입자와 완전히 다른 '위상(Topology)'을 갖고 있기 때문에, '무한대 문제'도 전혀 다른 형태로 나타난다. 대충 말하자면, 끈은 유한한 길이를 가지고 있으므로, 여기에 가까이 접근해도 힘의 크기가 무한대로 커지지 않는다. 끈 근처에서 힘은 L²에 반비례하는데, 여기서 L은 끈의 길이고, 구체적인 값은 약 '10^-33cm(플랑크 길이)'이며, 무한대를 잘라내는 역할을 한다. 끈은 무한히 작은 점과 달리 유한한 길이를 갖고 있기 때문에, 무한대는 끈을 따라 무마되고 모든 물리량은 유한한 값을 갖게 된다.

끈이론에서 무한대가 나타나지 않는 것은 직관적으로 자명해 보이지만, 사실 수학적으로 증명하려면 매우 어렵고 까다로운 절차를 거쳐야 한다. 이 과정에는 '타원 모듈라 함수(Elliptic Modular Function)'이라 부르는 유별난 함수가 등장하는데, 이 함수는 오직 10차원 또는 26차원에서만 성립한다. '타원 모듈라 함수'는 끈이론이 오직 10차원 또는 26차원에서 성립하는 이유를 설명해 주고 있다. '초끈이론'은 10차원, '보존 끈이론(Bosonic String Theory)'는 26차원에서 존재해야 무한대 문제가 발생하지 않는다.

8-2. 끈의 초대칭

그러나 '끈(String)'의 '위상(Phase)'만으로는 모든 '무한대 문제'를 해결할 수 없다. 남아 있는 무한대를 먼저 제거하려면 끈이론의 또 다른 특징인 '대칭성(Symmetry)'을 십분 활용해야 한다. '끈이론'에서 '대칭(Symmetry)'은 남아 있는 '무한대 문제(infinity Problem)'와 또 다른 문제인 '비정상성 문제(Anomaly Problem)'를 상쇄시키는 중요한 역할을 한다. 끈은 지금까지 알려진 모든 과학적 대상들 중에서 가장 높은 '대칭성(Symmetry)'을 가지고 있다. 원자 세계의 입자들을 가장 우아하게 시키는 방법이 바로 '대칭에 의한 분류'이다.

일단 대부분의 '무한대 문제'는 끈의 '위상(Phase)'으로 제거된다고 이미 말했다. 그리고 끈의 '위상'을 이용하여 제거한 후에도 여전히 남아 있는 '무한대'는 두 가지 형태로 분류할 수 있는데, '페르미온의 상호작용에서 나타나는 무한대'와 '보존의 상호작용에서 나타나는 무한대'가 바로 그것이다. 그런데 이 두 종류의 무한대는 항상 크기가 같고 부호는 반대이기 때문에 서로 정확하게 상쇄된다. 다시 말해서 '페르미온'과 '보존'에 의한 공헌도가 항상 반대이므로, 이론에 남아 있는 무한대가 말끔하게 사라진다는 것이다. 그러므로 초끈이론은 겉보기에만 그럴듯한 허황된 이론이 결코 아니다. '초끈이론'은 끈이론에 나타나는 '무한대 문제'까지 깨끗하게 해결해 주는 이상적인 이론이며, 남아 있는 모든 입자들을 하나의 대칭으로 통합시켜준다.

'대칭성(Symmetry)'은 우리가 사용할 수 있는 도구들 중에서 가장 아름답고 강력한 도구이므로, 우주를 설명하는 이론은 아마도 가장 우아하고 가장 강력한 대칭성을 보유하고 있을 것으로 기대된다. 논리적으로 생각해 보면, 이것은 쿼크에 한정된 대칭이 아니라 자연에서 발견되는 '모든 종류의 입자'들을 포함하는 초대형 대칭일 것이다. 다시 말해서, 물리학자들이 원하는 것은 모든 입자들을 자기들끼리 바꿔치기해도 형태가 변하지 않는, 그런 방정식이다. 이러한 대칭을 '초대칭(Super-symetry)'라고 하며, 초대칭을 갖고 있는 끈을 '초끈(Superstring)'이라고 한다. '초대칭'은 물리학에 등장하는 모든 입자들을 맞바꾸는 유일한 대칭으로서, 우주를 구성하는 모든 입자들을 하나의 통일된 체계로 나열하는 가장 우아한 방법이다.

8-2-1. 페르미온과 보존

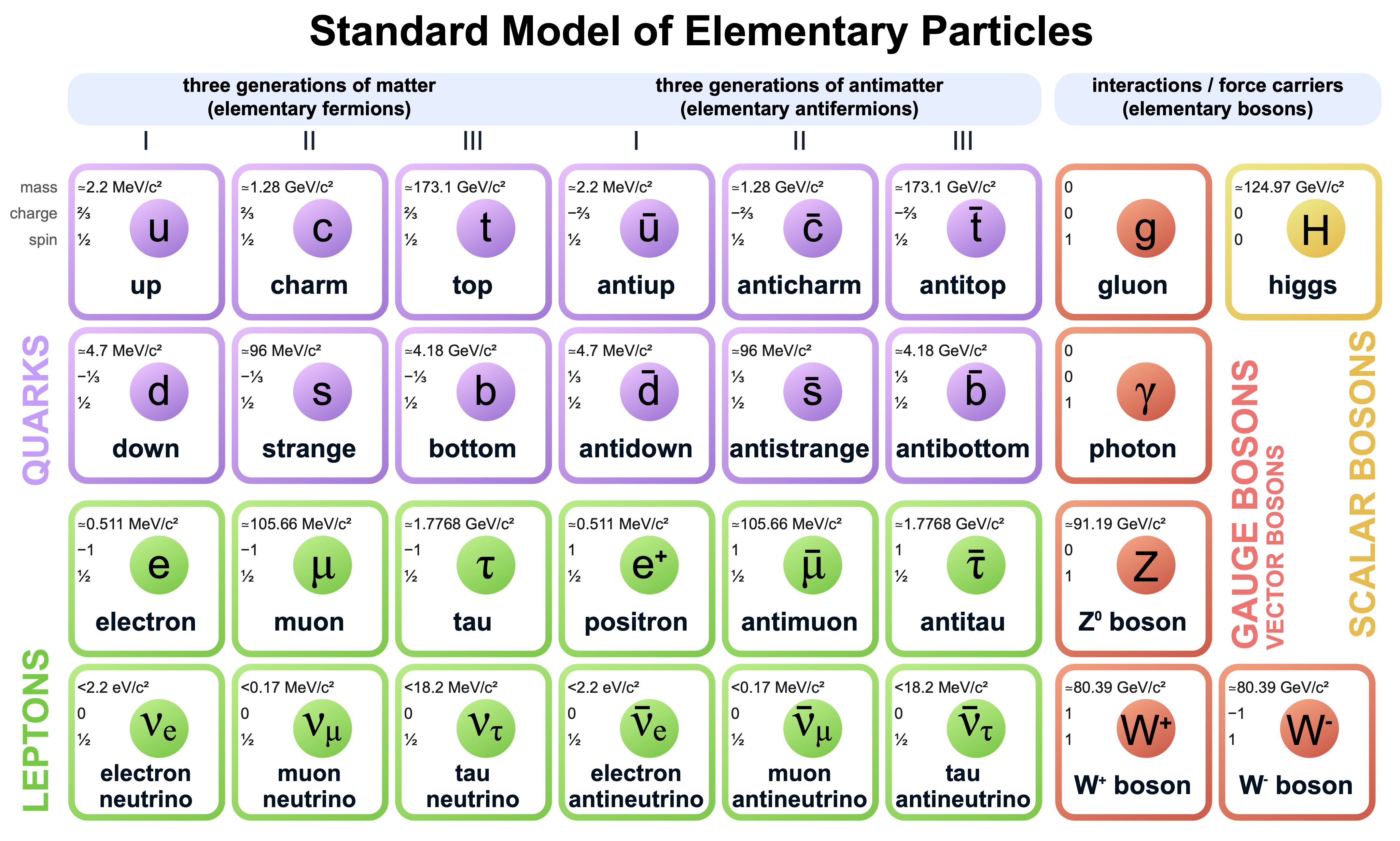
우주에 존재하는 모든 입자들은 '스핀 값'에 따라 '페르미온(Fermion)'과 '보존(Boson)'의 두 종류로 구분될 수 있다. 입자는 다양한 빠르기로 팽이처럼 회전하고 있는데, 이 특성을 간단한 숫자로 표현한 것이 스핀이다. 예컨대 '전자기력'을 매개하는 빛의 입자인 '광자(Photon)'과, '약력'을 매개하는 'W-보존(W-Boson)', 그리고 '강력'을 매개하는 '글루온(Gluon)'의 스핀은 모두 1이며, 중력을 매개하는 중력자의 스핀은 2이다. 이와 같이 스핀이 정수인 입자들을 '보존(Boson)'이라고 한다. 또한 물질을 구성하는 모든 입자들은 1/2, 3/2, 5/2등 반정수의 스핀을 가지고 있는데, 이들을 '페르미온(Fermion)'이라고 한다. '초대칭(Supersymmetry)'는 '보존'과 '페르미온'을 연결하는 대칭이므로 '힘(매개입자)'과 '물질(물질 입자)'을 연결시켜주는 대칭이라고 할 수 있다.

8-2-2. 초대칭짝 (Sparticle)

'초대칭 이론'에 의하면 모든 입자들은 파트너를 가지고 있다. 각각의 '페르미온(Fermion)'들은 특정한 '보존(Boson)'과 초대칭짝을 이룬다. 모든 소립자들은 '페르미온' 아니면 '보존'에 속하므로, 간단한 대칭 속에 모든 입자들을 아우를 수 있는 이론은 '초대칭 이론' 뿐이다. 초대칭짝에 해당하는 입자는 아직 한 번도 발견된 적이 없지만, 물리학자들은 이 가상의 파트너 입자들에게 이미 이름까지 붙여놓았다. 초대칭짝 입자의 이름은 대개 s로 시작한다. 예컨대, '전자(Electrion)'의 초대칭짝은 '셀렉트론(Selectron)'이고, '쿼크(Quark)'의 초대칭짝은 '스쿼크(Squark)'이고, '렙톤(Lepton)'의 초대칭짝은 '슬렙톤(Slepton)'이다. 일반적으로 '이미 알려져 있는 입자들(쿼크, 렙톤, 중력자, 광자 등)'의 초대칭짝을 통칭해 '초대칭 입자(Superparticle)'이라고 한다. 그러나 '입자가속기(particle accelerator)'에서는 이런 입자들이 아직 발견된 적이 없다. 아마도 입자가속기의 출력이 모자라기 때문일 것이다.

8-2-3. '초대칭'은 실험적인 증거가 확보되었는가?

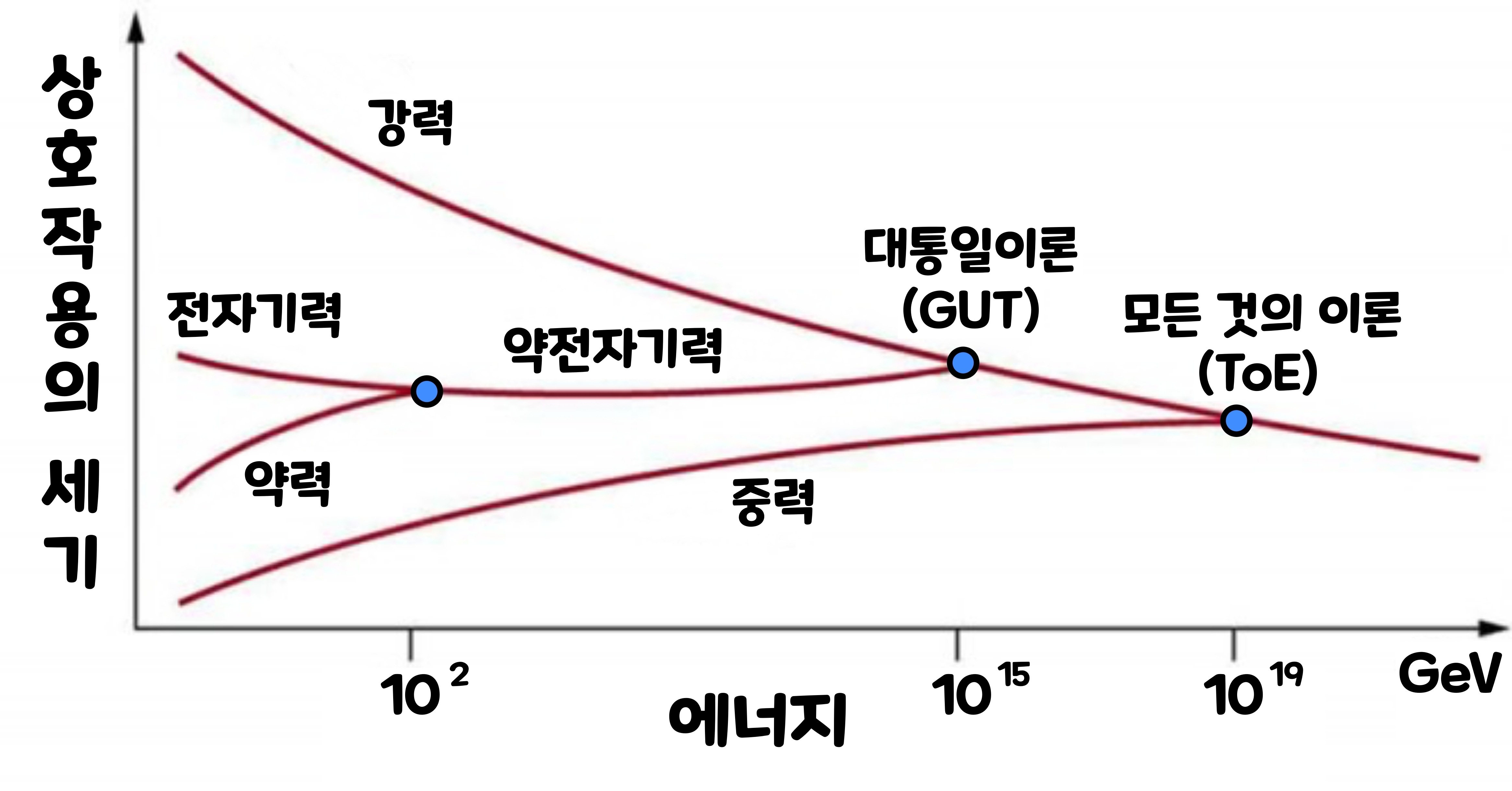
초대칭은 난처한 문제를 해결해 주는 강력한 아이디어임에 틀림없지만, 아직은 실험적인 증거가 확보되지 않은 상태이다. 물리학자들은 중력을 제외한 세 종류의 힘의 세기가 모두 다르다는 사실을 잘 알고 있다. 낮은 에너지에서 강력은 약력보다 30배쯤 강하고, 전자기력보다는 100배쯤 강하다. 그러나 이러한 대소 관계가 항상 성립하는 것은 아니다. 빅뱅이 일어나던 무렵에 모든 힘들은 똑같은 크기였을 것으로 추정되고 있다. 빅뱅과 비슷한 고에너지 상태로 가면 이들의 세기는 거의 하나의 값으로 수렴한다. 이것은 초대칭이론을 도입했을 때 얻어지는 결과로서, 이로부터 초대칭이론이 통일장 이론의 핵심적인 요소임을 짐작할 수 있다.

물리학자들은 '빅뱅(Big Bang)'이 일어나던 무렵까지 거슬러 올라가 세 힘의 크기를 계산하는 데 성공했다. 표준모형에 의거한 계산 결과에 의하면 우주 초창기에 전자기력, 약력, 강력의 크기는 거의 비슷했지만 완전히 같지는 않았다. 그러나 여기에 초대칭을 도입하면 세 힘의 크기가 완전히 같아지면서, 모든 물리학자의 희망봉인 '통일장이론'에 한 걸음 더 다가서게 된다. 물론 이것은 초대칭이론의 직접적인 증거가 될 수는 없지만, 지금까지 알려진 물리학과 초대칭 사이에 어떤 모순이 유발되지 않는 것만은 확실하다.

9. 끈이론이 직면한 어려운 문제

1984년에 시작된 끈이론 열풍은 한동안 전 세계의 이론물리학계를 휩쓸면서 최대의 화두로 자리 잡았다. 그러나 1990년대 중반으로 들어들 즈음, 끈이론 추종자들의 열정은 많이 식어 있었다. 그들은 어려운 문제를 저만치 제쳐두고, 쉬운 문제만을 집중 공략하고 있었다. 끈이론이 직면한 어려운 문제들 중 하나는 끈을 서술하는 방정식이 무려 수십억 개나 된다는 점이었다. 시공간의 차원을 줄이는 방법에 따라, 끈이론의 해는 4차원뿐만 아니라 다양한 차원에서 얻어질 수 있으며, 각각의 해는 나름대로 타당한 우주를 서술하고 있었다. 물리학자들은 홍수처럼 쏟아지는 해에 익사할 지경이었다. 게다가 그 많은 해들 중 대부분은 현재의 우주와 거의 비슷했다. 3차원 공간에 걸맞는 끈이론의 해는 무수히 많지만, 이들 중 하나를 골라낼 마땅한 방법이 없다.

우리의 우주는 빅뱅이 일어난 후, 오랜 세월 동안 식어 저-에너지 세계가 되었다. 저-에너지 세계에서는 초대칭의 존재를 확인할 수 없다. '전자'의 초대칭짝인 '셀렉트론(Slectron)'을 본 사람은 아무도 없다. 그래서 초끈이론을 현실 세계에 적용하려면, 어쩔 수 없이 '초대칭(Supersymmetry)'을 붕괴시켜야 한다. 만일 초대칭이 붕괴되지 않았다면, 입자는 자신의 초대칭짝과 동일한 질량을 가지고 있어야 한다. 물리학자들은 자연의 초대칭이 이미 붕괴되어 초대칭짝들의 질량이 현재의 입자 가속기로는 감지할 수 없을 정도로 커졌다고 믿고 있다. 그러나 초대칭이 어떤 과정을 통해 붕괴되었는지는 아직 미지로 남아 있다.

9-1. 다섯 개의 끈이론

문제는 이것뿐만이 아니다. 수학적으로 자체 모순이 없는 끈이론도 다섯 개나 된다. 그렇다면 우리 우주는 다섯 가지의 통일장이론에 따라 운영되었단 걸까? 끈이론은 왜 다섯 가지나 존재하는 걸까?

끈이론	끈의 형태	대칭성
I형 초끈이론(Type I)	열린 끈, 닫힌 끈 모두 허용	-
IIA형 초끈이론(Type IIA)	닫힌 끈만 허용	-
IIB형 초끈이론(Type IIB)	닫힌 끈만 허용	-
이형끈이론 - E8×E8	닫힌 끈만 허용	대칭의 규모가 매우 크다.
이형끈이론 - O(32)대칭군	닫힌 끈만 허용	대칭의 규모가 매우 크다

I형 초끈이론(Type I String Theory): '가브리엘레 베네치아노(Gabriele Veneziano)'와 '미히코 스즈키(Mahiko Suzuki)'의 초창기 이론에 입각한 초끈이론은 'I형 초끈이론(Type I String Theory)'이라고 한다. 'I형 초끈이론'은 두 개의 끝을 갖는 끈인 '열린 끈(Open String)'과 원형으로 감긴 끈인 '닫힌 끈(Closed String)'을 모두 허용하고 있다. 1970년대의 물리학자들은 I형 초끈이론을 집중적으로 연구했다.
II형 초끈이론(Type II String Theory): '케이지 키카와(Keiji Kikawa)'와 '미치오 카쿠(Michio Kaku)'는 '닫힌 끈(Closed String)'만으로도 자체 모순이 없는 이론을 만들 수 있다는 사실을 입증하였다. 이 이론은 현재 'II형 초끈이론(Type II String Theory)'으로 알려져 있으며, 닫힌 끈들은 두 개의 작은 닫힌 끈으로 분열하면서 상호작용을 주고받는다. 'II형 초끈이론(Type II String Theory'에는 'IIA형 초끈이론(Type IIA String Theory)'와 'IIB형 초끈이론(Type IIB String Theory)' 두 종류가 있다.
이형끈이론(Heterotic String Theory): 가장 현실적인 끈이론으로는 프린스턴 연구팀의 '데이비드 그로스', '에밀 마티넥(Emil Martinec)', '라이언 롬(Ryan Rohm)', '제프리 하비(Jeffrey Harvey)'가 구축한 '이형끈이론(Heterotic String Theory)'을 들 수 있다. 닫힌 끈만을 허용하는 '이형끈이론'은 'E₈×E₈' 또는 'O(32)대칭군'을 채용하고 있는데, 대칭의 규모가 매우 커서 GUT까지도 포함할 수 있다. 1980년대와 1990년대에 물리학자들이 특별한 부연 설명 없이 끈이론을 언급하면 대부분 '이형끈이론'을 말하는 것이라고 보면 된다. 이론에 담겨 있는 대칭성이 워낙 높아서 표준이론을 분석하기에 아주 적절했기 때문이다.

9-2. 초중력의 수수께끼

9-2-1. 초중력 이론(Supergravity Theory)

끈이론이 다섯 종류나 가능하다는 것 말고도, 끈이론을 향한 과정에서 잊혀져 가는 문제가 하나 있었다. 1976년에 '스토니브룩'의 뉴욕주립대에서 끈이론을 연구하던 세 사람의 물리학자 '피터 반 노이벤후이젠(Peter Van Nieuwenhuizen)'과 '세르지오 페라(Sergio Ferrara)', '다니엘 프리드먼(Daniel Freedman)'은 아인슈타인의 중력이론에서 원래의 중력장에 '중력자(Graviton)'의 초대칭짝 '초중력자(Gravitino)'를 도입하면, 초대칭을 보유한 중력이론으로 전환될 수 있음을 증명하였다. 흔히 '초중력(Supergravity)'으로 일컬어지는 '초중력 이론(Supergravity Theory)'은 '끈(String)'이 아닌 '점(Point)' 입자에 기초한 이론이었다. 무한히 많은 진동과 공명 패턴을 갖고 있는 '초끈이론'과 달리, '초중력 이론'은 단 두 개의 입자만을 가지고 있었다.

그 후 1978년에 파리 고등사범학교의 '유진 크리머(Eugene Cremmer)'와 '조엘 셔크', '버나들 줄리아(Bernard Julia)'는 11차원에서 가장 일반적인 '초중력 이론'을 구축하였고, 1970년대 후반부터 1980년대 초반에 걸쳐 '초중력'은 통일장이론의 강력한 후보로 부상하게 되었다. '스티븐 호킹(Stephen William Hawking)'은 '아이작 뉴턴(Asaac Newton)'의 뒤를 이어 케임브리지 대학 수학과의 '루카스 석좌교수(Lucasian Chari)'로 취임하면서 "이론물리학의 끝이 보이고 있다.'는 취임사를 남겼다. 그러나 얼마 지나지 않아 '초중력'은 다른 이론들을 사장시켰던 '무한대 문제'에 똑같이 직면하게 되었다. 다른 이론과 비교했을 때 무한대가 그렇게 많이 등장하지는 않았지만, 어쨌든 '초중력 이론'에서 무한대는 끝까지 제거되지 않은 채 물리학자들을 괴롭혔다.

9-2-2. 초막 이론(Super-Membrane Theory)

'초대칭(Supersymmetry)'을 채용한 또 하나의 이론으로는 11차원 '초막 이론(Super-membrane Theory)'를 들 수 있다. 끈은 1차원적인 객체로서 길이만을 갖고 있었지만, '초막(Super-membrane)'은 표면을 갖고 있기 때문에 2차원, 또는 그 이상의 객체가 될 수 없다. 지금까지 알려진 바에 의하면, 11차원에서 성립하는 초막 이론은 '2차원 막(2-brane)'과 '5차원 막(5-brane)' 두 가지가 있다.

그러나 '초막 이론(Super-Membrane Theory)'도 나름대로의 문제점을 가지고 있었다. 이 이론은 다루기가 엄청 까다로울 뿐만 아니라, 양자역학 버전으로 가면 '무한대 문제'가 빠지지 않고 등장한다. 이리하여 1990년대 중반에 접어들면서 물리학자들은 지독한 수수께끼에 직면하게 되었다. 10차원의 끈이론은 왜 다섯 개나 존재하는가? 11차원에서 성립하는 이론은 왜 '초중력'과 '초막 이론' 두 개나 있는 건가? 해답은 알 수 없었지만, 한 가지 확실한 것은 이들 모두가 '초대칭(Super-Symetry)'을 보유하고 있다는 사실은 알 수 있었다.

10. M-이론(M-Theory)

10-1. 'M-이론'의 탄생

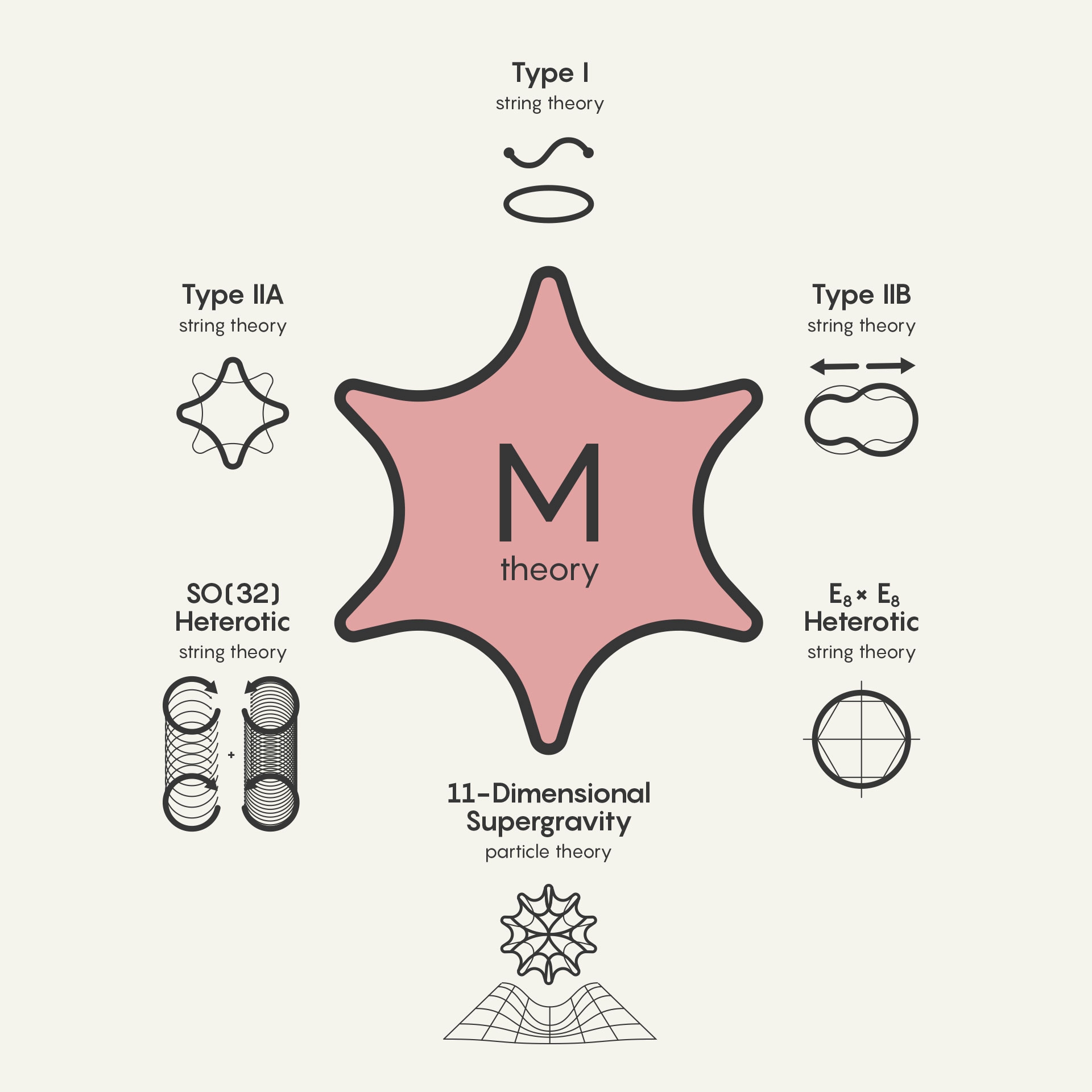
그러다 1994년에 물리학계에 초대형 핵폭탄이 떨어졌다. 프린스턴의 '에드워드 위튼(Edward Witten, 1951~)'과 케임브리지 대학의 '폴 타운센드(Paul Townsend, 1951~)'가 혁명적인 아이디어를 제안하여 지지부진하던 끈이론에 새로운 활력을 불어넣은 것이다. 이들은 10차원 끈이론이 '그 기원을 알 수 없는 신비한 11차원 끈이론'의 근사적인 서술에 지나지 않는다는 놀라운 사실을 알아냈다. 이와 더불어 '에드워드 위튼'은 그가 찾아낸 '11차원 막 이론'에서 하나의 차원을 작은 영역 속에 말아 넣으면 10차원의 'IIA형 초끈이론(Type IIA String Theory)'이 된다는 것을 증명하였다.

그 후 얼마 지나지 않아, 다섯 개의 끈이론들은 '에드워드 위튼'이 발견했던 '신비한 11차원 끈이론'의 다른 근사적 이론이었음이 밝혀졌다. 11차원에는 여러 종류의 '막(Membrane)'이 존재할 수 있었으므로, '에드워드 위튼'은 이 새로운 이론을 'M-Theory(M-이론)'이라고 불렀다. 그러나 나중에 알고 보니 'M-이론'은 '초중력 이론(Supergravity Theory)'까지 설명하는 그야말로 만능의 이론이었다.

11차원 초중력 이론은 '중력자'와 그 초대칭짝인 '초중력자' 이렇게 두 개의 입자만은 이론이다. 그러나 'M-이론'에는 질량이 제각기 다른 입자들이 무한정 등장하며, 각 질량은 11차원 막에 주름을 형성하는 고유한 진동에 대응한다. 'M-이론'에서 하나의 차원을 작은 영역에 돌돌 말아 넣으면 '끈이론'이 자연스럽게 유도된다. 이러한 차원 축소 과정은 다섯 가지 방법으로 진행될 수 있으며, 각각은 이미 알려져 있는 다섯 개의 10차원 끈이론에 대응되었다. 이로써 물리학자들은 '10차원의 모든 끈이론'과 '초중력 이론'을 모두 하나로 통합하는 '통일 이론'을 갖게 된 셈이다. 'M-이론(M-Theory)'은 정말로 물리학자들이 오랫동안 꿈꿔왔던 '모든 것의 이론(ToE: Theory of Everything)'일지도 모른다. 이것은 진정 물리학의 역사가 낳은 걸작 중에 걸작이 아닐 수 없다.

10-2. 'M-이론'은 물리학의 끝인가?

만약 M-이론이 성공을 거둔다면, M-이론은 정말로 '모든 것의 이론(ToE: Theory of Everything)'이 되는 걸까? 물리학은 여기에서 끝나는 것일까? 이에 대한 답은 '아니다'라는 것이다. 체스의 규칙을 잘 안다고 해서, 체스 마스터가 될 수 없는 것처럼, 우주가 운영되는 법칙을 모두 알았다고 해서 우주의 모든 것을 이해할 수는 없다. 'M-이론'은 우주의 시작에 관하여 많은 정보를 제공하고 있지만, M-이론을 우주론에 적용하는 것이 아직 시기상조일지도 모른다. M-이론이 제시하고 있는 '모형(Model)' 자체가 아직 완성되지 않기 때문이다. M-이론이 '모든 것의 이론'으로 발전할 가능성은 얼마든지 있다고 생각되지만, 이론이 완성된 모습을 보려면 아직 한참을 기다려야 한다.

저작자표시 비영리 변경금지