'열역학'의 기초
'열역학(Thermodynamics)'은 물질의 상태(state) 변화에 따라 발생하는 '열(Heat)'과 '일(Work)'의 양을 열역학 법칙으로 정의되는 '에너지(Energy)'와 '엔트로피(Entropy)' 등의 열역학적 변수들을 이용하여 분석하는 학문이다. '열역학'은 원자나 분자의 존재가 아직 증명되지 않았던 시대에, '열을 어떻게 효율적으로 동력으로 바꿀까?'라는 문제와 밀접하게 관련되면서 발전해 왔다.
0. 목차
- '온도'란 무엇인가?
- 샤를의 법칙(Charles's Law)
- 보일의 법칙(Boyle's law)
- 이상 기체 상태 방정식
- '열'이란 무엇인가?
- 열역학 제1법칙 (에너지 보존의 법칙)
- 열역학 제2법칙 (엔트로피의 법칙)

1. '온도'란 무엇인가?
어떤 물체든 잘게 분해해 나가면, '원자(Atom)'나 '분자(Molecule)' 등 미세한 입자로 이루어져 있다. 그러면 물질의 온도가 변할 때, 그 물체를 구성하는 원자와 분자는 어떻게 변할까?
'물(Water)'을 예로 들어보자. 물속에는 수많은 '물 분자(H2O)'가 자유롭게 움직이고 있다. 온도를 올리면, 물 분자가 물속에서 튀어나와 공기 속으로 날아가 '수증기'가 된다. 반대로 물이 0℃까지 차가워지면, 활발하게 움직이던 물 분자가 규칙적으로 늘어서 '결정(Crystal)'이 된다. 이것이 바로 '얼음(Ice)'이다. 결정이 된 '물 분자'는 쉽게 움직일 수 없다. 하지만 이 상태에서 물 분자는 그 자리에서 격렬하게 진동하고 있다. 이처럼 물질을 구성하는 원자와 분자는 항상 움직이고 있으며, 결코 멈추는 일이 없다. 이것을 '열운동(Thermal Motion)'이라고 한다.
그리고 온도가 높아질수록 물체 내부에 있는 원자와 분자의 움직임은 격렬해지고, 온도가 낮아질수록 물체 내부에 있는 원자와 분자의 움직임이 느려진다. 즉 '온도(Temperature)'란 '물체에 포함되어 있는 입자 운동의 활발한 정도'를 나타낸 것이다. 물이 액체와 고체로 뭉쳐있는 것은 '분자 사이의 인력'인 '분자력(분자간력)' 때문이다. 물 분자는 이 인력에 묶여서 쉽게 돌아다닐 수 없다. 그러나 분자의 운동이 격력해지면, 분자는 '분자 사이의 인력'에 대항해 움직일 수 있게 된다. 액체의 물에서는 분자가 자유롭게 이동할 수 있지만 아직 묶여있는 상태이다. 분자의 운동이 더 격렬해지면, 인력을 뿌리치고 물속에서 물 분자가 튀어 오르게 된다.
1-1. 공기 중에는 '뜨거운 분자'도 있고 '차가운 분자'도 있다.
'온도'는 '원자나 분자의 움직임의 활발한 정도'라고 설명하였다. 그렇다면 어떤 온도의 기체 속에 포함된 분자의 속도는 모두 같을까? 예컨대, 1m3당 분자가 몇 개 밖에 없다면, 그것들이 공기 속을 같은 속도로 움직이고 있다고 해도 이상할 것이 없다. 하지만 실제 공기 속에는 1m3당 1019개 이상의 원자와 분자가 포함되어 있고, 그것들이 서로 충돌을 거듭하면 날아다니고 있다. 따라서 분자끼리 충돌할 때마다, 그 속도는 변할 것인데, 이런 상황에서 모든 분자의 속도가 같다고 생각하기는 어렵다. 즉, 어떤 온도의 기체 속에 포함된 분자의 속도는 일정하지 않다. 공기 속에서 원자나 분자끼리 충돌함으로써, '빠르게 움직이는 분자(뜨거운 분자)'에서부터 '느리게 움직이는 분자(차가운 분자)'까지 모두 존재한다.
'기체의 온도'는 이처럼 다양한 속도로 움직이는 기체 분자의 속도 분포로 정해진다. 온도가 높은 공기 속에서는 전체적으로 빠르게 움직이는 분자의 비율이 높고, 반대로 온도가 낮은 공기 속에서는 전체적으로 느리게 움직이는 분자의 비율이 높다. 이처럼 기체 분자의 속도에는 '편차(변량에서 평균을 뺀 값)'가 있다. 그리고 이 편차는 영국의 물리학자 '제임스 맥스웰(James Clerk Maxwell, 1831~1879)'이 밝힌 '맥스웰 분포(Maxwell's Distribution)'를 따른다.
또 같은 온도에서도 기체 분자의 질량이 다르면, 속도 분포에도 차이가 보인다. 같은 속도라도 질량이 큰 입자가 큰 운동에너지를 갖게 되는 것이다. 따라서 같은 온도의 기체라면, 질량이 큰 기체 분자로 이루어진 기체 쪽이 느리게 움직이는 분자의 비율이 높다.

2. 샤를의 법칙
공기는 따뜻해지면 상승하고 차가워지면 하강한다. 이 성질을 이용하여 만든 탈것이 바로 '기구(balloon)'이다. 공기를 데우면, 공기에 포함된 기체 분자는 움직임이 활발해져 넓은 범위로 퍼진다. 그 결과 부피가 늘어나 밀도가 낮아짐으로써, 가벼워져서 상승한다. 반대로 공기를 차갑게 하면, 공기에 포함된 기체 분자의 움직임이 느려져, 그만큼 주변의 활발하게 움직이는 분자에 밀려 좁은 범위에 몰린다. 그 결과, 부피가 줄어들어 밀도가 높아짐으로써, 무거워져 하강한다.
이처럼 기체의 온도를 올리거나 내리면 기체가 팽창하거나 수축한다. 프랑스의 물리학자인 '자크 샤를(Jacques Alexandre César Charles, 1746~1823)'은 '수소 기구(hydrogen ballon)'을 연구하다가 1787년에 '샤를의 법칙'을 발견했다. '샤를의 법칙(Charles's Law)'은 기체의 압력을 일정하게 한 상태에서는 기체의 부피가 온도에 비례한다는 법칙이다.
2-1. 온도가 올라가면 부피는 늘어난다.
'샤를의 법칙(Charles's Law)'에 따르면, 기체의 부피는 1℃ 내려갈 때마다 0℃에서의 부피의 273분의 1만큼 감소한다. 그래서 '자크 샤를'은 기체의 온도를 계속 내리면 약 -273℃에서는 부피가 0이 되어 온도의 '하한선'에 이른다고 예측했다. 그리고 그 온도를 '절대 영도(Absolute Zero)'라고 불렀다. 그 후의 연구를 통해 '절대 영도'는 영하 -273.15℃로 정해졌다. 하지만 실제의 물질은 크기가 있는 입자로 이루어져 있기 때문에, '절대 영도'에서도 부피가 0이 되지는 않는다.
하지만 일상생활에서 온도를 나타낼 때는, 물이 얼음이 되는 온도인 0℃와 물이 끓는 온도인 100℃를 기준으로 한 '섭씨온도'를 사용하는 경우가 많다. 하지만 과학계에서는 '절대 영도'를 기준으로 한 '절대 온도'의 단위인 'K(캘빈)'이라는 단위가 많이 사용되며, '절대 온도'의 정식 명칭은 '열역학 온도'이다. '절대온도'는 '섭씨온도'에 273.15℃를 더한 값이기 때문에 0℃는 약 273K가 되고, 100℃는 약 373℃가 된다. 또 1℃의 간격과 1K의 간격은 같다.
3. 보일의 법칙(Boyle's law)
위에서는 압력이 일정할 때, 기체의 부피는 '온도(Temperature)'에 비례한다는 '샤를의 법칙(Charles's Law)'에 대해 알아보았다. 이번에는 '압력(Pressure)'이 변할 때, 기체에 어떤 상태의 변화가 일어나는지 살펴보자.
3-1. 압력의 정체
그렇다면 '기체의 압력'이란 과연 무엇일까? 우리는 '기체의 압력'을 잘 의식하지 못하고 있지만, 지구에서 생활하고 있는 한 '대기압(공기 무게에 의해 생기는 대기의 압력)'을 사방팔방에서 받고 있다. 대기압은 1cm2당 약 1kg중의 무게로, 상당히 커다란 힘이다. 예컨대, 욕실의 타일 벽에 붙이는 흡반이 벽에서 떨어지지 않는 것도 대기압 때문이다. 흡반을 벽에 눌러 붙여 벽과의 사이에서 공기를 빼내면, 대기압(공기의 압력)'은 흡반을 벽 쪽으로만 누르게 되어, 흡반이 벽에 달라붙는 것이다. 또 풍선이 오므라들지 않는 것도 풍선 내부의 공기 압력 덕분이다. '풍선 내부의 공기 압력'과 '대기압'의 압력이 평형을 이룸으로써 풍선은 크기를 유지하게 된다.
'기체의 압력'의 원인은 분자 수준에서 생각하면 '기체 분자의 충돌'이라고 할 수 있다. 기체 분자 1개의 충돌로 인해 생기는 힘은 약하지만, 무수한 기체 분자가 끊임없이 충돌하면 무시할 수 없는 커다란 압력이 된다.
3-2. '압력'과 '부피'가 반비례한다.
용기에 기체를 넣고, 무게는 무시할 수 있는 뚜껑으로 밀폐했다고 하자. 뚜껑이 정지되어 있다면, '용기 속에 밀폐되어 있는 기체의 압력'과 '대기압'은 평형을 이루고 있을 것이다. 대기압의 2배가 되도록 뚜껑 위에 추를 얹으면, '용기 속에 밀폐되어 있는 기체의 압력'도 2배가 된다. 그런데 '기체의 압력'은 '기체 분자의 충돌'에 의해 생긴다고 했다. 그러면 기체의 압력이 2배가 되었을 때 '분자 수준'에서는 어떤 변화가 일어날까?
'용기 속에 밀폐되어 있는 기체의 압력'을 2배로 하기 위해서는, '기체 분자가 충돌할 때 물체에 가해지는 힘의 크기'를 2개를 하든가, '기체 분자가 충돌하는 빈도'를 2배로 하면 된다. '온도(기체 분자의 속도)'와 '기체 분자의 수'가 압력을 가한 전후에 변하지 않는다고 생각하면, 용기의 부피를 반으로 줄이면 '기체 분자가 충돌하는 빈도'는 2배가 될 것이다. 부피를 절반으로 하면 '기체 분자의 밀도'가 2배가 되기 때문에, 기체 분자가 용기의 벽에 충돌하는 빈도도 2배가 될 것이다.
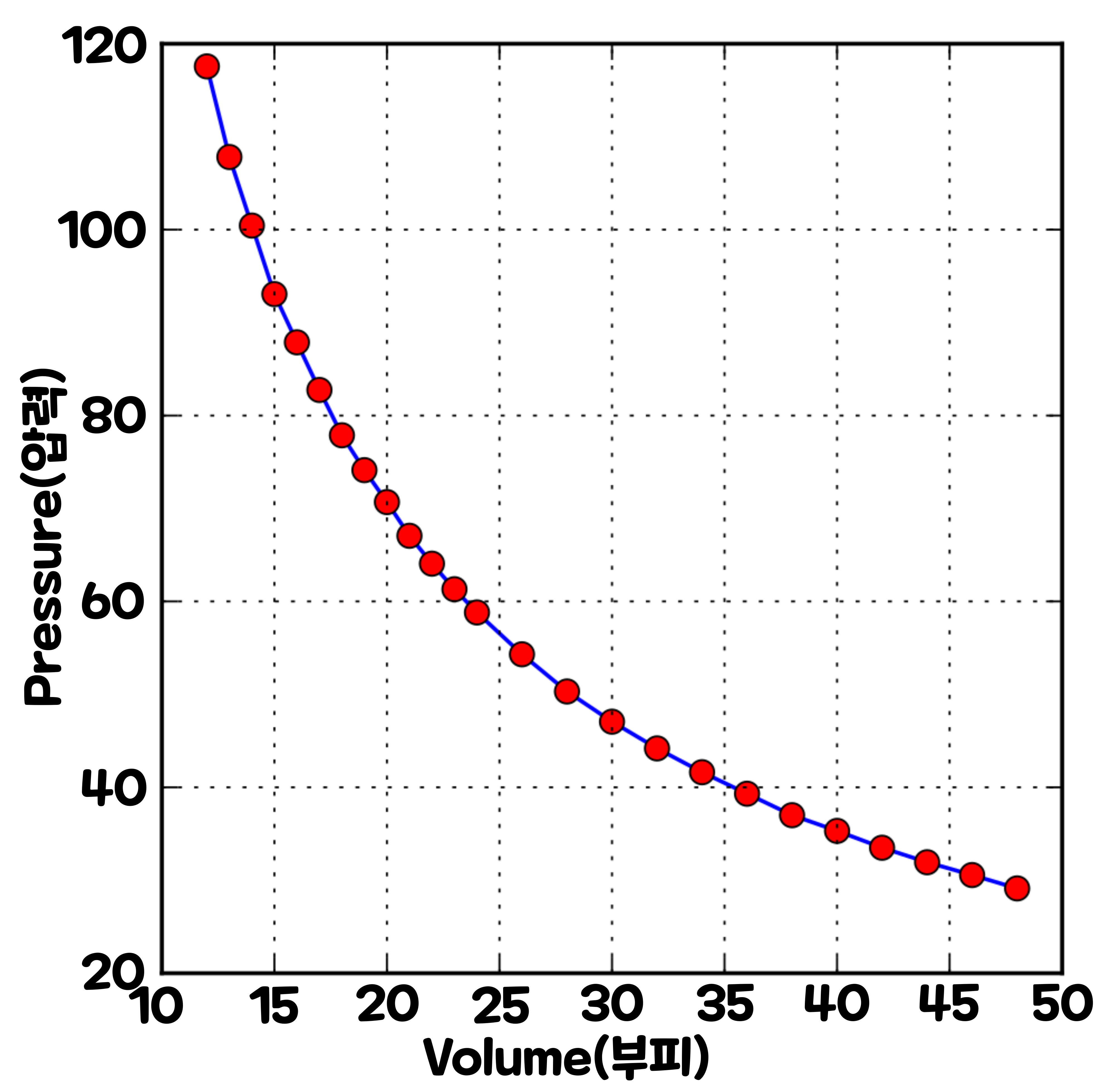
결국 온도와 기체 분자의 수가 일정하게 유지되고 있다면, 기체의 부피가 절반이 되면 압력은 2배가 되고, 부피가 2배가 되면 압력은 절반이 된다. 즉, 기체의 '부피(Volume)'와 '압력(Pressure)'은 반비례한다. 이것이 영국이 물리학자 '로버트 보일(Robert Boyle, 1627~1691)'이 1662년에 발견한 '보일의 법칙(Boyle's Law)'이다.
4. 이상 기체 상태 방정식
4-1. 압력을 2배로 하는 방법
먼저 '샤를의 법칙(Charles's Law)'을 통해, 온도와 분자량이 일정하다는 조건 아래에서는 부피를 절반으로 함으로써 기체 분자가 충돌하는 빈도가 2배가 되어, 압력이 2개가 될 수 있음을 살펴보았다. 그리고 '보일의 법칙'을 통해, '용기 속에 있는 기체'의 압력을 2배로 하기 위해서는 '기체 분자가 충돌할 때 물체에 가해지는 힘의 크기'를 2배로 하거나 '기체 분자가 충돌하는 빈도'를 2배로 해야 함도 살펴보았다.
만약 용기 내의 온도와 분자의 양을 자유롭게 바꿀 수 있다면, 부피를 유지하면서 '압력을 2배로 하는 방법'은 없을까? 부피를 유지하면서 기체의 압력을 높일 수 있다. '용기 속의 기체 분자의 수'를 늘려 기체 분자가 벽에 충돌하는 빈도를 늘린다든지, '기체의 온도'를 올려서 기체 분자가 충돌할 때 가해지는 힘을 크게 해도 압력이 커진다.
4-2. 이상 기체 상태 방정식
부피와 온도가 비례한다는 '샤를의 법칙(Charles's Law)'과, 부피와 압력이 반비례한다는 '보일의 법칙'을 결합시켜보자. 그러면, '기체의 부피는 온도에 비례하고 압력에 반비례한다.'는 '보일-샤를의 법칙'(Boyle-Charles' Law)'이 탄생한다.
'보일'과 '샤를'이 한 실험에서는, 기체 분자의 양이 같다면, 어떤 기체든 부피-압력-온도의 관계는 같았다고 한다. 결국 부피-압력-온도 가운데 2개의 상태만 정해지면, 나머지 하나의 상태가 결정된다. 더 나아가 기체의 압력과 부피는 각각 '기체 분자의 양'에도 비례할 것이다. 결국 기체의 '압력(P)', 부피(V)', '온도(T)', '기체 분자의 양(n)' 사이에는 'PV/T=일정'과 같은 관계가 성립한다. 즉, 'PV=nRT(R은 비례상수)'과 같은 관계가 성립하고, 이 식을 '이상 기체 상태 방정식(ideal gas equation)'이라고 한다.
'이상 기체 상태 방정식(Ideal Gas Equation)'은 '샤를의 법칙', '보일의 법칙'을 따르는 어떤 기체이든 성립한다. 단, '이상 기체(Ideal Gas)'라고 하듯이 계산값과 실제값 사이에는 오차가 생길 수 있다. 예컨대 예컨대 극단적으로 저온이라든지 고밀도 상태가 되면, '기체 분자 자체의 크기'나 '분자 사이에 작용하는 인력'의 영향으로, 오차를 무시할 수 없게 되기 때문이다. 그래서 이상 기체에서는 분자끼리 끌어당기는 힘인 '판데르발스 힘'이 작용하지 않는 것으로 가정되어 있다.
4-3. 판데르발스 상태 방정식
그래서 물리학자 '요하너스 디데릭 판 데르 발스(Johannes Diderik van der Waals, 1937~1923)'는 19세기 후반에 실제의 기체에 보다 가까운 값을 계산할 수 있는 새로운 식인 '판데르발스 상태 방정식(Van der Waals equation of state)'을 제안했다. '판데르발스 상태 방정식'의 좌변과 우변을 비교하면, 이 식은 이상 기체의 상태 방정식에 '압력과 부피를 보정하는 계산'이 추가되었음을 알 수 있다. 실제의 기체에서는 분자끼리 당기는 만큼 압력이 줄고, 분자의 크기만큼 기체의 부피가 늘어나는 점이 고려되어 있다. 그래서 보다 정확한 시뮬레이션을 할 때는 '판데르발스 상태 방정식'을 사용해야 한다.

5. '열'의 전달
5-1. '열'이란 무엇인가?
이번에는 '열(heat)'이 무엇인지 생각해 보자. 예컨대 0℃의 공기와 30℃의 공기를 비교하면, 30℃의 공기가 더 뜨겁다. '온도'는 '입자 움직임의 활발한 정도'이므로, 0℃의 공기보다 30℃의 공기에 포함된 입자의 움직임이 더 빠르다. 공기 속에서 살고 있는 우리의 몸에는 항상 기체 분자가 충돌하고 있다. 따라서, 0℃의 공기보다 30℃의 공기 속에 있을 때, 공기 속에 포함되어 있는 기체 분자로부터 더 큰 충격을 받게 된다. 즉 '열(heat)'은 기체 분자 등의 미세한 입자의 충돌로 전해진다. 바로 '에너지(Energy)'이다.
하지만 반드시 '온도'가 높다고 '뜨거운 것(열이 많은 것)'은 아니다. 예컨대 같은 온도라도 50℃의 목욕물에는 뜨거워서 들어갈 수 없지만, 50℃의 사우나라면 견딜 수가 있다. 목욕물에 포함되어 있는 물 분자는 매우 고밀도이기 때문에, 뜨거운 물에 닿을 때 피부에 닿는 물 분자의 수가 매우 많기 때문이다. 하지만 기체로 된 물 분자의 밀도는 액체의 물 분자에 비하면 크게 낮기 때문에, 피부에 닿는 물 분자의 수가 적다. 그 결과, 분자로부터 전해진 에너지가 작아져 열을 적게 느끼게 된다.
5-2. 접촉한 물체에서의 열전달
우리는 생활에서 몸을 따뜻하기 위해 난방을 하거나 따뜻한 물을 마신다. 반대로 몸을 차게 하기 위해서는 에어컨을 사용해 차가운 바람을 쐬거나 물을 적신 수건을 써서 시원하게 한다. 이처럼 우리는 '온도차가 있는 물체 사이에서는 열이 이동한다'는 사실을 경험을 통해 알고 있다. 그러면 열이 물체 사이를 이동한다는 것은 과연 무엇일까?
예컨대 따뜻한 캔 커피를 차가운 손에 쥔 경우를 생각해 보자. 이 경우, 열은 따뜻한 캔 커피에서 차가운 손으로 이동할 것이다. 뜨거운 캔의 표면에 있는 금속 원자는 그 온도에 맞게 활발하게 진동하고 있다. 한편, 차가운 손에 있는 손을 구성하는 분자는 따뜻한 캔 커피의 금속 분자보다 활발하게 진동하고 있지는 않다. 이 상태에서 캔과 손의 경계에는 활발한 정도가 다른 원자나 분자끼리 접촉한다. 원자나 분자끼리 몇 차례 충돌하면, 그로 인해 차가운 손을 구성하는 분자가 금속 원자의 진동에 의해 동요되어 서서히 활발하게 진동하게 된다. 결국 금속 원자의 '운동 에너지(Kinetic energy)'의 일부가 손을 구성하는 분자에 전해지는 것이다. 최종적으로는 캔과 손의 온도차가 없어질 때까지 '운동 에너지'가 전해진다.
이번에는 냄비에 불로 열을 가해 물을 데우는 경우를 생각해 보자. 이 경우, '불꽃 속에 있는 활발히 움직이는 분자'와 '바닥의 금속 원자'가 흔들린다. (불꽃에서 나온 전자기파에 의한 가열 효과도 있음) 금속 원자의 진동이 냄비 전체로 확대되면, 냄비 안에 있는 물 분자도 활발히 진동해서 물의 온도가 올라간다.
5-3. 전자기파에 의한 열전달
지구는 태양과 접촉해 있지 않지만, 태양에 의해 덥혀진다. 이처럼 열이 전해지는 데는 반드시 물체끼리 직접 접촉해야 하는 것은 아니다. 텅 빈 우주 공간을 지나 열이 전달될 수 있는 것은 '전자기파(electromagnetic waves)'와 관련되어 있다. 전자기파가 물체에 닿아 흡수되면, 물체를 구성하고 있는 입자인 '전자(electron)'가 요동한다. 전자기파 중에서 적외선과 마이크로파는 전자를 통해 분자 전체를 요동시키고, 물질의 온도를 올리는 작용을 한다. 이처럼 열은 전자기파에 의해서도 전해진다.
그리고 전자기파를 통해 열이 전달되는 것과 반대되는 과정도 있다. 모든 물체는 그 온도에 따른 파장의 전자기파를 방출하고 있다. 이것을 '열 복사(thermal radiation)'라고 한다. 일반적으로 물체의 온도가 높을수록 파장이 짧은 전자기파의 성분이 많이 복사된다.
6. 열역학 제1법칙 (에너지 보존의 법칙)
6-1. 열과 일은 서로 변환된다.
지금까지 보았듯이 '열(heat)'은 원자나 분자 같은 작은 '입자의 충돌에 의해 전해지는 에너지'이다. 하지만 과거에는 열을 물질이라고 생각하던 시대가 있었다. 그 가상의 물질을 '칼로릭(caloric)'이라고 불렀는데, 물체가 뜨거워지는 이유는 물체 속에 칼로릭이 주입되었기 때문이라고 생각했다. 물체를 문지를 때 발생하는 마찰열은 물체에 숨겨진 칼로릭이 겉으로 드러났기 때문이라고 주장되었다.
열은 '물질(matter)'이 아니라 '에너지(energy)'임을 이해하게 된 계기는 19세기 중반, 영국의 '제임스 줄(James Joule, 1818~1889)'과 독일의 '율리우스 마이어(Julius Robert von Mayer, 1814~1878)'의 연구였다. '물을 휘젓거나 압축하면 온도가 상승한다는 것'은 '일과 열이 같은 효과를 나타낸다는 것'이다. 그들은 이점에 착안하여, 그것들이 양적으로도 일정한 비율로 변환된다고 주장했다. '일'은 '힘을 가해서 물체를 움직이는 것'을 말하며 '힘×이동 거리'로 표시된다.
6-2. 열역학 제1법칙의 탄생
이러한 연구로 도출된 결과가 바로 '열역학 제1법칙'이다. '열역학 제1법칙'은 열역학 분야의 '에너지 보존 법칙(Law of energy conservation)'이라고도 할 수 있다. '열역학 제1법칙'은 '△U=W+Q'이다. (△U=물체 내부 에너지의 증가량, W=물체에 대해 한 일, Q=외부에서 물체에 가해진 열) 여기에서 '물체'라고 썼지만, 더 정확하게는 '계(system)'이다. '계(system)'는 고체·액체·기체에 국한됨이 없이, 어떤 주목할 부분에 포함된 물체의 집합을 가리킨다.
여기에서 말하는 '물체'는 전체적으로 정지해 있는 상태를 말한다. 따라서 전체적으로 '운동 에너지(Kinetic energy)'는 아니다. 하지만 물체를 구성하는 입자는 '열운동(Thermal Motion)'을 하고 있을 것이다. 이처럼 물질이 가진 원자나 분자 수준의 에너지를 물리학에서는 '내부 에너지(Internal Energy)'라고 한다.
6-3. 일과 열 모두 '내부 에너지'를 증가시킬 수 있다.
이 식은 물체에 대해 일을 하든 열을 가하든, 두 경우 모두 물체의 '내부 에너지'가 증가함을 나타낸다. 기체를 예로 생각해 보자.
- '기체를 덥히면(열을 가하면)' 기체 분자 운동 에너지가 증가해서 온도가 상승한다.
- '기체를 압축하면(일을 하면)' 기체 분자가 충돌하는 빈도가 증가하여 온도가 상승한다.
즉, 두 경우 모두 '내부 에너지'가 증가한다.
6-4. 일은 '내부 에너지'를 증가시킬 수도 있고 감소시킬 수도 있다.
피스톤이 달린 용기에 기체가 들어있는 경우를 생각해 보자.
- 피스톤이 달린 용기에 기체를 넣고 피스톤을 누르면, 기체 분자에 힘이 가해져 속도가 올라간다. 기체 분자의 운동 에너지가 증가하므로 온도가 상승한다. 즉 '내부 에너지(Internal energy)'가 증가한다.
- 반대로 피스톤이 달린 용기에 기체를 넣고 피스톤을 당기면, 기체 분자는 에너지를 소비해 속도가 줄어든다. 기체 분자의 운동 에너지가 감소하므로 온도가 줄어든다. 즉 '내부 에너지(Internal energy)'가 줄어든다.
즉, '일(work)'은 '내부 에너지'를 증가시킬 수도 있고 감소시킬 수도 있다.
6-5. 줄의 '열의 일당량' 측정 장치
아래의 그림은 '제임스 줄(James Joule, 1818~1889)'이 '열(Heat)'과 '일(Work)'이 변환될 수 있다는 점을 나타내기 위해 실시한 실험 장치를 그린 것이다. 손잡이를 돌려 추를 자유 낙하시키면, 물통에 들어 있는 회전 날개가 돌며 물을 휘저어 수온을 상승시킨다. 추의 '위치 에너지'가 '운동 에너지'로 바뀌고, 그것이 마찰열로 변환된 것이다.
추를 들어 올린 높이와 상승한 수온을 계산하면, 물 1g은 1℃ 상승시키는 열량을 얻기 위해 해야 하는 일의 값을 알 수 있다. 줄은 실험을 거듭해 1cal(칼로리)의 열량이 약 4.2J(줄)의 '일당량(Mechanical Equivalent)'이라는 측정값을 얻었다. 이 수치는 현재에도 통용되고 있다. 이렇게 해서 '열'과 '역학적 에너지'가 같은 단위로 계산될 수 있음을 밝혔다.
1cal(칼로리)는 '표준 대기압(1atm)'에서 물 1g을 1℃ 상승시키는 데 필요한 열량이다. 단, 칼로리라는 단위에는 문제점도 있다. 몇℃의 물을 1℃ 올리느냐에 따라 필요한 열량이 다르기 때문이다. 그래서 국제도량형총회에서 결정한 'IS 단위계(국제단위계)'에서는 열량의 단위로 '줄(J)'을 쓰게 되어 있다.

6-6. 산업 혁명의 계기가 된 '열기관'
열역학은 열을 어떻게 동력으로 바꾸는가라는 과제와 함께 발전해 온 분야라고 할 수 있다. '열'을 연속적으로 일로 바꾸는 장치를 '열기관(Heat Engine)'이라고 한다. 18세기에는 연료를 태우는 방법으로 액체를 끓이고, 그 증기로 피스톤을 움직이는 '증기 기관(Steam Engine)'이 발달해 '산업 혁명(Industrial Revolution)'을 일으켰다.
'스털링 엔진(stirling engine)'은 '열기관(heat engine)'의 한 종류로서, 공기 등 기체 형태의 '작동 유체(working fluid)'에 열을 가하여 반복적으로 압축하고 팽창시키면서 피스톤이 움직인다. 이 피스톤의 끝에 톱니바퀴 같은 것을 연결하면, 회전 운동의 동력으로도 이용할 수 있다. 실제로 '스털링 엔진'은 배나 잠수함의 엔진으로 이용된다. 기계가 수축하고 팽창하는 과정에서 '열역학 제1법칙'의 식은 반드시 성립한다. 열역학 제1법칙'은 '△U=W+Q'이다. (△U=물체 내부 에너지의 증가량, W=물체에 대해 한 일, Q=외부에서 물체에 가해진 열)
- Q=△U-W: 기체에 열을 가하면, 그 열은 기체의 내부 에너지를 증가시키거나 기체가 외부에 하는 일이 된다.
- W=△U-Q: 기체에 일을 해 주면, 그 일은 기체의 에너지를 증가시키거나 외부에 열로 방출된다.
- Q=0, △U=W: 기체의 열을 외부로부터 차단하는 경우, 행하는 일이 모두 기체의 '내부 에너지'의 변화로 이어지는 '단열과정(외부와 열전달이 일어나지 않는 과정)'이 일어난다.
- Q=W, △U=0: 기체의 온도를 일정하게 유지하면서 행하는 '등온 과정(온도를 일정하게 유지하고 압력과 부피를 변화시키는 과정)'이라는 것도 있다.
'열역학 제1법칙'에 따르면, 열을 가하지 않고 기체에 일을 시키면 W는 '음(-)'이 된다. 즉 기체의 내부 에너지가 줄어든다. 따라서 기체에 계속 일을 시키기 위해서는 외부에서 계속 열을 공급해야 한다. 게다가 열기관에는 '열역학 제1법칙'을 충족시키는 것만이 아니라, 또 하나의 제약이 있음이 밝혀졌다. 이 문제에 대해서는 '열역학 제2법칙'에서 설명한다.
7. 열역학 제2법칙 (엔트로피의 법칙)
7-1. '제1종 영구 기관'은 불가능하다.
'영구 기관(Perpetual motion machine)'은 연료를 제공하지 않고 일을 계속하는 가상의 기관이다. 현재에는 열역학 법칙을 위배하는 이유로 영구기관이 불가능하다는 사실이 알려졌지만, 과거에는 '영구 기관'이 모색되었다. 유명한 과학자들도 '영구 기관'에 대해 연구했는데, 예를 들면 '보일의 법칙'으로 유명한 '로버트 보일(Robert Boyle)'도 '모세관 현상'을 이용한 것을 고안하였다.
초기에는 '무(無)'에서 에너지를 얻는 유형의 영구 기관인 '제1종 영구 기관'이 고안되었다. 하지만 '열역학 제1법칙(에너지 보존의 법칙)'이 등장하면서 '제1종 영구 기관'은 부정되었다. 하지만 영구 기관을 만들려는 사람들은 물러서지 않았다. 이번에는 '열역학 제1법칙(에너지 보존 법칙)'에 어긋나지 않는 새로운 방식의 영구 기관을 고안했다. 예를 들면 다음과 같은 자동차이다.
7-2. '제2종 영구 기관'도 불가능하다.
7-2-1. 연료를 사용하지 않는 자동차는 가능한가?
이 자동차에는 액체를 끓이고 그 증기를 회전력으로 바꾸는 엔진인 '증기 기관'이 달려 있다. 액체는 '끓는 점이 15℃인 것(15℃에서 끓어서 증기가 되는 것)'이 사용된다. 주위에 있는 20℃의 공기를 이용해 이 액체를 덥히면 액체를 끓일 수 있다. 액체를 덥힌다는 것은 공기에서 액체로 열이 이동하는 것이다. 그만큼 온도가 내려간 공기는 예컨대 19℃가 되면, 공기는 자동차 밖으로 배출된다.
증기 기관을 움직여 자동차를 주행시키는 일을 하면, 증기 기관이 가진 에너지는 그만큼 줄어든다. 연료도 그 무엇도 보급하지 않고 증기 기관이 계속 움직인다면, 에너지를 스스로 만들어 내는 '제1종 영구 기관'이 되지만, 이 자동차는 줄어든 만큼의 에너지를 주위의 공기로부터 보충하므로 '열역학 제1법칙(에너지 보존 법칙)'에 어긋나지 않는다. 만약 이런 일이 가능하다면, 자동차는 연료를 사용하지 않고 달릴 수 있게 된다. 하지만 이런 자동차는 다음과 같은 이유 때문에 불가능하다.
7-2-2. 열을 버릴 곳이 없어, 자동차는 계속 움직일 수 없다.
'열(heat)'을 '일(work)'로 바꾸는 '열기관'이 '열'에서 '일'로 변환을 계속하려면, 원리상으로는 증기 등의 '작업 물질(일을 시키는 물질)'이 외부에 대해 일을 한 다음, 최초의 상태로 되돌아가야 한다. 결국, 작업 물질을 차갑게 해서 원래의 상태로 되돌려, 밀어 올린 피스톤을 원래의 위치까지 내려야 한다. 그렇지 않으면 다시 피스톤을 밀어 올릴 수 없다. 즉, 일을 할 수 없다.
위에서 말한 자동차의 증기 기관에서는 15℃에서 끓는 액체를 사용했다. 따라서 자동차 주위에 있는 20℃의 공기로 이 액체를 덥히면, 액체를 끓여서 증기를 만들고 피스톤을 밀어 올릴 수 있었다. 이 증기 기관이 다시 한번 일을 하려면 증기를 식혀 액체로 되돌려야 한다. 그러려면 이 액체의 끓는점인 15℃보다 낮은 온도의 공기가 필요해진다. 하지만 주위에는 그런 저온의 공기가 없다. 결국, 열을 버릴 곳이 없는 것이다.
냉장고 같은 것으로 식히면 되지 않느냐고 생각할지도 모르겠지만, 그러면 에너지를 사용하게 되므로 에너지를 사용하지 않고 움직이는 자동차가 아니게 된다. 결국, 지금까지 말한 자동차의 증기 기관은 최초 상태로 되돌아가는 일을 반복할 수 없다.
7-2-3. 물이 저절로 끓어오는 일은 있을 수 없다.
만약 20℃의 공기를 써서 증기를 15℃까지 식힐 수 있다면, 그것은 '저온의 물체'에서 '고온의 물체'로 열이 이동한 것과 같다. 이것은 60℃의 물이 든 컵을 기온 20℃의 방 안에 두었더니, 공기로부터 물로 열이 저절로 이동해 끓어오르는 것처럼 있을 수 없는 현상이다. 즉, 위에서 말한 자동차가 움직이기 위해서는 자연 현상에 위배되는 현상이 일어날 수 있어야 한다.
독일의 물리학자 '루돌프 클라우지우스(Rudolf Clausius, 1822~1888)' 등은 열의 이동에 관한 자연계의 법칙을 '열역학 제2법칙'으로 나타냈다. '열역학 제2법칙(The Second Law of Thermodynamics)'이란 '열은 고온의 물체에서 저온의 물체로 이동하지만, 그 반대의 이동은 저절로 일어나지 않는다.'는 것이다. 열역학 제1법칙'에는 어긋나지 않지만 '열역학 제2법칙'에 위배되는 영구 기관을 '제2종 영구 기관'이라고 한다. '열역학 제2법칙'이 등장함으로써, '열역학 제1법칙'을 교묘히 피한 영구 기관인 '제2종 영구 기관' 연구자들도 더 이상 돌파구가 없어지고 말았다.
'톰슨의 원리(Thomson's principle)'에서는 '하나의 열원에서 열을 제거하고 아무런 영향도 남기지 않고 이것을 전부 일로 변환하는 것은 불가능하다.'고 표현한다. '루돌프 클라우지우스'의 표현과는 다르지만, '톰슨의 원리'와 '열역학 제2법칙'이 물리적으로는 같다는 점도 증명되었다.
7-3. 엔트로피 증가의 법칙
열역학 제2법칙'은 왜 성립할까? 상식에 비추어 보면 당연한 것처럼 보이지만, 사실 신기한 법칙이기도 하다. '열역학 제2법칙'이 성립하는 이유를 분자 차원에서 설명하려고 한 사람이 오스트리아의 물리학자 '루트비히 볼츠만(Ludwig Boltzmann, 1844~1906)'이다.
물에 잉크를 넣으면, 처음에는 일부에만 머물러 있던 잉크가 오랜 시간 후에는 전체로 퍼져나갈 것이다. 물과 잉크가 각기 분리되어 있던 것이 점차 무질서하게 섞이는 것이다. 우리 주위에 존재하는 물질은 물과 잉크가 분리되어 있는 것처럼 '질서 잡힌 상태'에서 물과 잉크가 섞인 '무질서한 상태'로 되는 숙명을 안고 있다. 이 무질서함과 난잡함의 정도를 나타내는 개념을 '엔트로피(entropy)'라고 한다. '물과 잉크가 분리되어 있는 상태'는 '엔트로피가 낮은 상태(질서 있는 상태)'라고 할 수 있다. 반대로 '물과 잉크가 섞여 있는 상태'는 '엔트로피가 높은 상태(무질서한 상태)'라고 할 수 있다. 한번 섞인 물과 잉크를 원래대로 되돌리기 위해서는 어떤 조작을 해야 한다. 하지만 외부에서 어떤 조작을 해도, 외부도 포함된 전체 엔트로피는 항상 증가할 뿐 결코 감소하지 않는다. 이것을 '엔트로피 증가의 법칙(Law of Entropy Increase)'이라고 한다.
실은 열이 반드시 온도가 높은 곳에서 낮은 곳으로 이동한다는 '열역학 제2법칙'은 '엔트로피 증가의 법칙'과 같은 내용을 나타낸다. '물체의 내부에서 온도차가 있는 상태'란, 부위에 따라 물체를 구성하는 원자 움직임의 격렬함에 차이가 있는 상태이다. 즉, 질서가 있는 상태로, 엔트로피가 작은 상태이다. 반대로 '물체의 내부에서 온도가 균일해진 상태'란, 부위에 따라 물체를 구성하는 원자 움직임의 격렬함이 전체로 흩어진 상태이다. 즉 무질서한 상태로, 엔트로피가 큰 상태이다. 전체의 온도가 균일해지도록, 열이 반드시 온도가 높은 곳에서 온도가 낮은 곳으로 이동하는 것은 엔트로피가 항상 증가하는 것과 같다.
7-4. 엔트로피와 생명
'생명(Life)'는 매우 질서 잡힌 복잡한 구조를 하고 있다. 그리고 지구의 역사 약 46억 년 동안, 단세포 생물처럼 단순한 생물에서부터 인간처럼 더 복잡한 구조를 가진 생물을 키워왔다. '생명을 만드는 것(고도의 질서 구조를 만드는 것)'은 '엔트로피의 감소'를 의미한다. 그러면 지구는 왜 낮은 엔트로피의 생명을 만들어내고, '진화(Evolution)'라는 엔트로피가 줄어드는 현상을 만들었을까?
지구와 생명은 외부로부터 영향이 없는 '독립계(Independent System)'가 아니다. 태양으로부터 에너지가 공급되고, 차가운 우주 공간에 여분의 에너지를 버린다. 열을 받은 우주 공간은 엔트로피가 증가하므로, 주위의 우주 공간까지 포함해 생각하면 결국 엔트로피는 증가하고 있는 것이다. 지구는 태양으로부터 빛과 열에너지를 받음으로써, '생명(Life)'이라는 질서 잡힌 구조를 만들 수 있다. 그리고 그 과정에서 발생한 '폐열(Waste Heat)'은 우주 공간에 버려진다. 같은 조건이라면 고온 쪽이 엔트로피가 높으므로, 결국 우주 공간에 엔트로피 증가라는 '대가'를 지불함으로써, 지구는 부분적으로 낮은 엔트로피의 상태인 '생명(life)'를 만들어 낼 수 있는 것이다. '생명의 탄생과 진화' 그리고 '문명의 진보'는 모두 '뜨거운 태양'과 '차가운 우주 공간' 덕분이라고 말할 수 있다. 하지만 진화를 고려해도, 엔트로피는 시간과 함께 증가하고 있다.