스도쿠(Sudoku)
'스도쿠(Sudoku)'는 누구나 쉽게 즐길 수 있는 숫자 퍼즐 게임이다. 숫자를 채워 넣는 퍼즐이지만, 수학은 물론 산수 지식마저도 필요하지 않다. 이런 점이 다양한 층에서 스도쿠를 즐길 수 있는 이유일 것이다. 그러나 그 이면에는 수학적인 심오함이 깃들어 있다. 스도쿠의 독특한 매력에 대해 알아보자.
0. 목차
- 스도쿠의 기본 규칙
- 스도쿠의 역사
- 스도쿠의 난제
- 컴퓨터가 푸는 스도쿠
- 스도쿠의 해법

1. 스도쿠의 기본 규칙
스도쿠의 규칙은 그리 복잡하지 않다. 9×9의 81개의 칸에 1~9 숫자를 넣어 나갈 뿐이다. 수평 방향으로 늘어선 9개의 칸을 '가로줄', 수직 방향으로 늘어선 9개의 칸을 '세로줄', 3칸×3칸 크기의 9칸으로 이루어진 영역을 '블록'이라고 한다. 그때 '가로줄', '세로줄', 3칸×3칸으로 구획된 9개의 '블록' 안에는 1~9의 숫자가 하나씩 들어간다. 즉, 같은 숫자가 2개 이상 들어가면 안 된다. 81개의 칸에는 20~30개 정도의 숫자가 들어 있으며, 그 상태를 '초기 배치'라고 한다. 이들 숫자를 단서로, 빈칸의 규칙에 따라 숫자로 채워 나간다. '스도쿠' 문제의 답은 반드시 하나뿐이다.
스도쿠 문제는 초기 배치에서 미리 들어 있는 숫자가 많을수록 난이도가 낮은 경향이 있다. 숫자를 좁혀 나가는 단서가 많아지기 때문이다. 하지만 초기 배치된 숫자의 수가 많아도 어려운 해법을 사용해야 풀 수 있는 고난이도 문제나, 초기 배치된 숫자가 적어도 기본적인 해법으로 풀 수 있는 저난이도 문제도 있다.
2. 스도쿠의 역사
그러면 스도쿠는 어떻게 탄생했을까? 1979년 미국의 '잡지 델(Dell Magazine)'이 '넘버 플레이스(Number Place)'라는 이름의 퍼즐을 지면에 실었다. 이 퍼즐은 스도쿠와 똑같은 것이다. 그러나 '넘버 플레이스'는 당시 미국에서 흥미를 끌지 못하고 바로 모습을 감추었다.
1984년 일본에서 퍼즐 전문지 출판사 '니콜리(Nikoli)'를 창설한 '가지 마키'씨는 잡지에 게재할 퍼즐을 참고하려고, 잡지 '델(Dell)'의 '과월호(잡지나 기타 정기 간행물에서 최근 호 이전에 발간된 것)'를 보고 있었다. 그 가운데 눈을 끈 것이 '넘버 플레이스(Number Place)'였다. 그래서 '가지 마키'씨는 자신이 만든 '넘버 플레이스'를 일본어로 '숫자는 한 번만 쓸 수 있다'는 이름으로 '월간 니콜리스트'에 게재했다. '숫자는 한 번만 쓸 수 있다.'는 일본어 문장 중에 '수(數)'와 '독(獨)'이라는 글자가 포함되어 있어, 일본어로 '스도쿠(數獨)'라는 약칭이 탄생했다. 그리고 독자들로부터 커다란 반응이 있었고, 순식간에 인기 퍼즐로 부동의 위치를 차지하게 되었다.
그러다 2004년 말, 스도쿠가 전 세계로 퍼져 나가는 계기가 된 사건이 있었다. 영국의 신문 '더 타임스(The Times)'에 '스도쿠'가 'Sudoku'라는 이름으로 게재된 것이다. 이를 계기로 영국에서도 Sudokurk 커다란 붐을 일으켰다. 붐은 영국에 그치지 않고 세계 각지로 퍼졌다. 그 후 세계 퍼즐 연맹이 주관하는 '세계 Sudoku 선수권'이 매년 열릴 정도로 인기 있는 퍼즐이 되었다.
2-1. 스도쿠의 기원은 '마방진'
역사를 조금 더 거슬러 올라가 보자. '스도쿠'의 기원이라고 생각되는 것은 '마방진(魔方陣)'이다. '마방진(魔方陣)'은 스도쿠와 같은 정사각형의 칸 안에 숫자를 늘어놓은 것인데, '어떤 행(가로줄)', '어떤 열(세로줄)', 대각선으로도 수의 합이 같은 성질이 있다. '마방진(魔方陣)'은 '마술'을 의미하는 '마(魔)'와 '사각형'을 의미하는 '방진(方陣)'을 조합한 글자로, 영어로는 '매직 스퀘어(Magic Square)'라고 하며 '신기한 사각의 수 나열'이라는 의미이다.
마방진의 기원은 고대 중국으로 거슬러 올라간다. 전설에 따르면, 기원전 2000년 무렵 중국의 가장 오래된 왕조로 일컬어지는 '하(夏)'의 '우왕(禹王)'이 황하의 홍수를 다스릴 때 '낙수(洛水)'라는 강에서 나온 거북의 등딱지에 무늬가 있음을 알았다고 한다. 그리고 무늬 속의 동그라미 개수를 각각 숫자로 바꾸어 3×3의 표로 나타내 보니, 표에는 1~9까지의 숫자가 하나씩 들어가면서 모든 행, 열, 대각선에 있는 수의 합이 15가 되었다. 흰 동그라미는 '홀수', 검은 동그라미는 '짝수'를 나낸다. '우왕'은 이 숫자의 배치에 신비성을 느끼고 이것을 '낙서(洛書)'라고 불렀다.

2-2. 마방진에 대한 흥미를 가진 사람들이 늘어났다.
낙서에 나타난 3×3의 마방진을 '3차 방진'이라고도 하는데, 그 후 중국에서는 '4차 방진', '5차 방진', 더 나아가 '10차 방진'까지 연구되었다. 낙서는 그 후, 점성술로서 '구성술(九星術)'로 발전했다. '구성술'은 일본의 '음양도(陰陽道)'에도 도입되었으며, 힌두교, 이슬람교, 유대교, 기독교에도 영향을 미쳤다.
또 마방진은 예술의 '모티브(Motive)'로도 사용된다. 예술 작품 안에 마방진이 그려진 최초의 예는 독일의 화가이며 철학자인 '알브레히트 뒤러(Albrecht Dürer, 1471~1528)'의 동판화 '멜랑콜리아(Melancholia)'라고 알려져 있다. 1514년에 제작된 이 작품에는 '4차 마방진'이이 그려져 있다. 4×4의 칸에는 1~16까지의 숫자가 들어 있으면 모든 행, 열, 대각선에 있는 수의 합이 34가 된다. 그리고 그것만 4등분 해도 각각의 수의 합계가 34가 되며, 중앙 4칸의 수의 합계도 34가 된다. 이처럼 마방진에 흥미를 가진 사람들이 동서양을 불문하고 늘어나, 마방진은 서서히 점성술에 이용되거나 예술의 모티브가 되었다.

2-3. 마방진은 수학 연구 대상이 되었다.
그뿐만 아니라 '마방진'은 수학의 연구 대상이 되었다. '마방진을 성립하는 수의 조합은 과연 몇 가지나 있는가?'라는 문제는 수학자를 괴롭히는 문제 중 하나이다.
- 2차 방진의 경우: 차수가 낮은 마방진부터 생각하면, 먼저 2차 방진은 존재하지 않는다.
- 3차 방진의 경우: 다음에 3차 방진은 회전과 반전에 의해 서로 같아지는 것을 제외하면 1종밖에 없다.
- 4차 방진의 경우: 차수를 하나 높인 4차 방진의 조합에 대해서는 880가지가 존재한다고 밝혀져 있다. '알브레히트 뒤러'가 그린 '멜랑콜리아'에 등장한 '4차 방진'도 그 가운데 하나이다.
- 5차 방진의 경우: 5차 방진이 되면 조합의 수는 셀 수 없을 정도로 많아진다. 따라서 많은 수학자가 이 난제에 몰두했다. 이 문제가 마침내 풀린 것은 1970년대로, 컴퓨터를 이용한 계산을 통해 '5차 방진'의 조합은 2억 7530만 5224종이 있음이 확인되었다.
| 차수 | 조합의 경우의 수 |
| 2차 방진 | 0 |
| 3차 방진 | 1 |
| 4차 방진 | 880 |
| 5차 방진 | 2억 7530만 5224 |
그 밖에도 '소수(Prime Number)'만을 사용한 '소수 마방진(Prime Number Magic Square)'과, 중심에 관해 대칭 위치에 있는 두 숫자의 합이 모두 같아지는 '대칭 마방진(Symmetry Magic Square)' 등 특수한 마방진이 고안되어 연구되었다.
2-4. 오일러의 '라틴 방진'이 나중에 '스도쿠'를 낳았다.
'마방진'에서 파생해 '스도쿠'로 한 걸음 다가선 것이 수학자 '레온하르트 오일러(Leonhard Euler, 1707~1783)'가 생각한 '라틴 방진(Latin Square)'이다. '레온하르트 오일러'는 'n행·n열의 칸 안에 1부터 n까지의 다른 숫자를 각각의 행과 열에 중복되지 않게 나열한다.'라는 규칙의 방진을 생각하고 그것을 '라틴 방진(Latin Square)'이라고 불렀다. n차 라틴 방진은 n개의 숫자를 사용하고, n차 마방진는 n2까지의 숫자를 사용한다. 그런데 9차 라틴방진은 스도쿠와 매우 비슷하다. 다른 점은 스도쿠의 경우, 행과 열만이 아니라, 블록도 1~9까지의 숫자를 하나씩 가지고 있다는 점이다. 결국 9차 라틴 방진에 블록의 묶음을 더하면 스도쿠가 된다.
마방진과 마찬가지로, '라틴 방진'과 '스도쿠'에도 수학 연구 대상이 되는 문제가 많이 있다. 흔히 연구되었던 문제는 '라틴방진과 스도쿠에는 어느 정도의 조합이 있는가?'이다. 먼저 '라틴 방진'부터 살펴보자 '2차 라틴 방진'은 2가지, '3차 라틴 방진'은 12가지, '4차 라틴 방진'은 576가지가 있다. 그러나 '5차 라틴 방진'이 되면 그 가짓수가 급격히 늘어난다. '레온하르트 오일러'는 죽기 전해인 1782년에 '5차 라틴 방진'이 16만 1280가지가 있음을 계산으로 제시했다. 한편 '9차 라틴 방진'에 대해서는 5524자 7514해 9615경 6892조 8425억 3122만 5600가지가 있음이 밝혀졌다. 이것은 28자릿수에 이르는 엄청나게 큰 수이다.
| 차수 | '라틴 방진'의 모든 경우의 수 |
| 2차 라틴 방진 | 2 |
| 3차 라틴 방진 | 12 |
| 4차 라틴 방진 | 576 |
| 5차 라틴 방진 | 16만 1280 |
| 6차 라틴 방진 | 8억 1285만 1200 |
| 7차 라틴 방진 | 61경 4794억 1990만 4000 |
| 8차 라틴 방진 | 1해 0877경 6032조 4590억 8295만 6800 |
| 9차 라틴 방진 | 5524자 7514해 9615경 6892조 8425억 3122만 5600 |
| 10차 라틴 방진 | 9간 9824구 3765양 8213자 0398해 7172경 5064조 7569억 2032만 0000 |
| 11차 라틴 방진 | 7769재 6683정 6171간 7701구 4410양 7444자 3467해 3423경 0682조 3110억 6560만 0000 |
3. 스도쿠의 난제
3-1. 스도쿠 조합의 가짓수는 몇 개인가?
그러면 '스도쿠 조합'의 수는 어떻게 될까? 먼저 3차 이하의 스도쿠는 존재하지 않는다. '4차 스도쿠'는 288가지가 있다. '4차 스도쿠'의 총수는 4차 라틴 방진의 576가지보다 적다. 이는 스도쿠에는 라틴 방진보다 엄격한 제약 조건이 있기 때문이다. 4차 스도쿠의 총수는 조음 어렵지만 계산할 수 있어, 예전에 '수학 올림픽'이나 '대학 입시 시험'에도 출제된 적이 있다고 한다. 그러면 9차 스도쿠에는 몇 가지 조합이 있을까? 슈퍼컴퓨터를 이용해 계산해 본 결과, 66해 7090경 3752조 0210억 7923만 6960가지로 밝혀졌다. 이것은 '9차 라틴 방진'의 28자릿수에는 미치지는 않지만 22자릿수나 되는 수이다.
더욱이 스도쿠의 경우 하나의 완성형에 대해 초기 배치로 어떤 숫자를 제시하는가에 따라 여러 개의 문제를 만들 수 있다. 바꾸어 말하면, 초기 배치가 달라도 최종적으로 같은 풀이에 이르는 문제가 여러 개 있었다는 뜻이다. 그러나 이런 초기 배치가 달라도 최종적으로 같은 풀이에 이르는 문제가 여러 개 있다는 뜻이다. 그러나 이런 초기 배치까지 고려한 스도쿠 문제의 총수를 산출하기는 현재로서는 매우 어렵다.
3-2. 초기에 배치하는 숫자의 최소 개수
또 한 가지, 수학자와 컴퓨터 과학자가 몰두해온 스도쿠 난제 중에는 '답이 반드시 하나로 정해질 때, 초기에 배치하는 숫자의 최소 개수는 몇 개인가?'라는 것이 있다. 이 문제의 답은 '17개'로 예상되고 있다. 왜냐하면 '초기 배치의 숫자 개수가 17개이며 답이 하나로 정해진 것'은 알려져 있었지만, '초기 배치의 숫자 개수가 16개이며 답이 하나로 정해진 것'은 알려져 있지 않았기 때문이다. 최소의 개수가 17임을 증명하기 위해서는 16개의 숫자가 배치된 문제를 샅샅이 찾아 풀어서, 답이 하나로 정해지는 것이 없음을 제시하면 된다. 그러나 이 방법으로는 슈퍼컴퓨터를 사용해도 계산량이 너무 많아 시간 안에 계산을 마칠 수 없다.
2012년 1월, 아일랜드 국립대학 더블린 캠퍼스의 수학자 '게리 맥과이어(Gary McGuire)'가 슈퍼컴퓨터와 복잡한 알고리즘을 구사해 '초기 배치의 숫자가 16개 이하이면 답은 하나로 정해지지 않는다.'고 결론지었다. '게리 맥과이어'는 2년에 걸쳐 계산해 이 결론에 도달했다고 한다. 효율적인 알고리즘을 사용해도 이처럼 시간이 걸린다는 점이 놀랍기만 하다. 여기에서 사용한 알고리즘의 기본 개념은 'DNA 염기 배열의 결정'이나 '신경 세포 네트워크 해석'에도 사용되고 있다. 스도쿠에 사용된 알고리즘은 앞으로 다른 분야에도 응용되어 성과를 거둘 가능성이 있다.
4. 컴퓨터가 푸는 스도쿠
스도쿠는 답이 하나로 정해지는 초기 배치이면 어떤 문제든 컴퓨터를 사용해 풀 수 있다. 그렇다면 컴퓨터는 어떤 알고리즘으로 스도쿠를 푸는 것일까? 컴퓨터가 스도쿠를 풀 때의 기본적인 알고리즘의 하나가 '백트래킹 법(Backtracking, 역추적 법)'이다. 백트래킹법의 알고리즘은 단순해, 가능한 조합을 하나씩 대입해 가면서 시험해 보는 것이다.
'백트래킹 법'으로 스도쿠의 답을 구하는 방법은 다음과 같다. 먼저 어떤 빈칸에 1을 넣는다. 그리고 다른 숫자와의 정합성을 얻을 수 있는 경우에는 다음 빈칸으로 옮겨가 거기에도 1을 넣는다. 그러나 다른 숫자와 모순이 생긴 경우에는 1을 빼고 2를 넣는다. 그래도 모순되면 3을 넣는다. 이처럼 숫자를 하나씩 늘려 가면서 정합성을 얻은 단계에서 다음 칸으로 옮겨간다. 만일 9까지 시도해도 정합성이 얻어지지 않는 경우에는 앞의 칸으로 돌아가 수를 하나씩 늘려 가며 같은 조작을 반복한다. 이런 방법으로 칸을 하나씩 살려 모두 조사하면 최종적으로 답에 도달한다.
4-1. 세계에서 가장 어려운 스도쿠 문제?
2013년 당시 일본 도쿄 대학에 근무하던 '와타나베 히로시' 박사는 '컴퓨터를 사용해 세계에서 가장 어려운 스도쿠 문제를 만드는 데 성공했다'고 발표했다. 이 문제는 '백트랭킹 법(Backtracking)'으로 풀면, 답을 찾을 때까지 수만 회 정도의 계산을 실행해서 사람이 푸는 것은 불가능하다고 생각되었다. 그러나 사람이 실제로 시도해 보니 의외일 정도로 쉽게 풀 수 있었다.
인간이 비교적 간단하게 풀 수 있었던 원인은 인간과 컴퓨터가 스도쿠를 푸는 방법의 차이에 있었다. '와타나베 히로시' 박사는 '백트래킹 법'에 의해 하나씩 대입해 가며 답을 찾을 때의 계산량'을 지표로 난이도를 판정하고 있었다. 하지만 인간은 보통 컴퓨터처럼 낱낱이 뒤져가며 답을 탐색하지 않고, 블록이나 열에 주목하면서 빈칸을 채워 간다. 결국 컴퓨터로 풀면 계산량이 많은 스도쿠 문제라도 인간에게 반드시 어렵다고 단정할 수는 없다. 물론 인간과 같은 방법으로 스도쿠를 푸는 알고리즘을 적용하면, 컴퓨터도 이 문제를 간단히 풀 수 있다. 같은 맥락으로 '인간에게 어려운 스도쿠 문제'도 만들 수는 있다. 다만 그러기 위해서는 인간의 사고를 정확하게 알고리즘에 담아야 한다. 이것은 기존의 방법으로는 되지 않는다. 그래서 '와타나베 히로시' 박사는 세계에서 가장 어려운 스도쿠를 만들려는 시도를 일시 중지했다고 한다.
4-2. 양자 컴퓨터에게 스도쿠는 쉽다.
'스도쿠'는 '조합 최적화 문제'의 일종이라고 할 수 있다. '조합 최적화 문제'란 주어진 조건에서 방대하게 있는 조합 가운데 최적인 조합을 찾아내는 문제로, 최근 사회적으로도 주목을 받고 있다. 유명한 예로 '방문 판매자 문제'가 있다. 이것은 1명의 세일즈맨이 복수의 고객을 모두 방문한 다음 회사로 돌아갈 때까지의 최단 경로를 찾아내는 문제이다. 단, 같은 길은 한 번만 지나갈 수 있다. 고객의 수가 늘어남에 따라 순회 경로의 조합 수는 폭발적으로 늘어나기 때문에, 최신 슈퍼컴퓨터를 사용해도 계산을 끝낼 수 없다. '자동차 내비게이션을 이용한 최적 경로 탐색', '전원의 부담이 같아지는 근무표 작성' 등도 조합 최적화 문제의 일종으로, 둘 다 조건이 약간 복잡해지기만 해도 방대한 양의 계산이 필요해진다는 문제점이 있었다.
그래서 주목된 것이 캐나다의 벤처 기업인 'D-웨이브 시스템(D-Wave Systems)'가 발표한 '어닐링 머신(Annealing Machine)'이다. 이것은 '조합 최적화 문제'에 특화된 양자 컴퓨터이다. 9×9의 스도쿠는 종래의 컴퓨터로 하나하나 찾아 계산하면 풀 수 있지만, '어닐링 머신(Annealing Machine)'을 이용해 '조합 최적화 문제'로 계산량이 많은 문제도 비교적 쉽게 해결할 수 있다.

5. 스도쿠의 해법
빈칸에 들어갈 숫자를 좁혀 가는 방법에는 '기본적인 방법'부터 '약간 어려운 방법', '고도의 방법'까지 여러 가지 종류가 있다. 기본적인 해법에는 '특정 블록에 주목하는 방법'과 '특정 열 또는 행에 주목하는 방법' 2가지가 있다. '특정 블록에 주목하는 방법'과 '특정 열에 주목하는 방법' 두 가지가 가장 기본적인 해법이지만, 이 밖에도 전부 10종 정도의 해법이 있다. 스도쿠 문제의 난이도는 사용하는 해법의 난이도에 따라 분류된다.
| 스도쿠의 해법 | 난이도 |
| 특정 블록에 주목하는 방법 | 기본적인 방법 |
| 특정 열 또는 행에 주목하는 방법 | 기본적인 방법 |
| 특정 칸에 주목하는 방법 | 약간 어려운 방법 |
| 어떻게 하든 이론 | 약간 어려운 방법 |
| 쌍둥이법 | 약간 어려운 방법 |
| 이게타 이론 | 약간 어려운 방법 |
| 황새치 | ? |
| 해파리 | ? |
| XY체인 | ? |
5-1. 특정 블록에 주목하는 방법
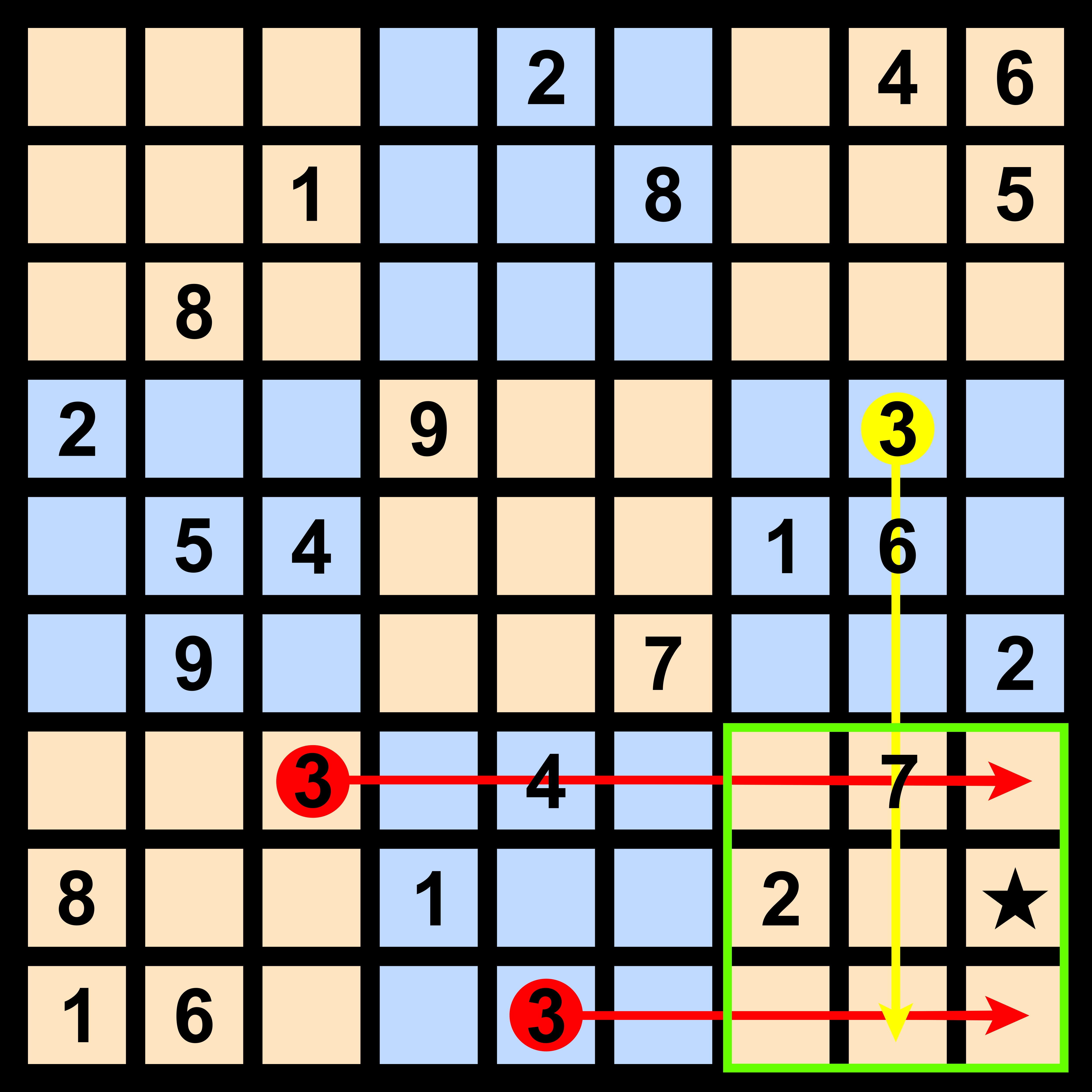
오른쪽 아래 블록에 주목해, 블록 안 어디에 3이 들어갈까를 생각하면 ★칸에 들어갈 수밖에 없음을 알 수 있다. '7번째 가로줄', '9번째 가로줄', '8번째 세로줄'에는 3이 이미 존재하기 때문에 이곳을 모두 제외하면 ★칸밖에 남지 않는다.
5-2. 특정 열 또는 행에 주목하는 방법
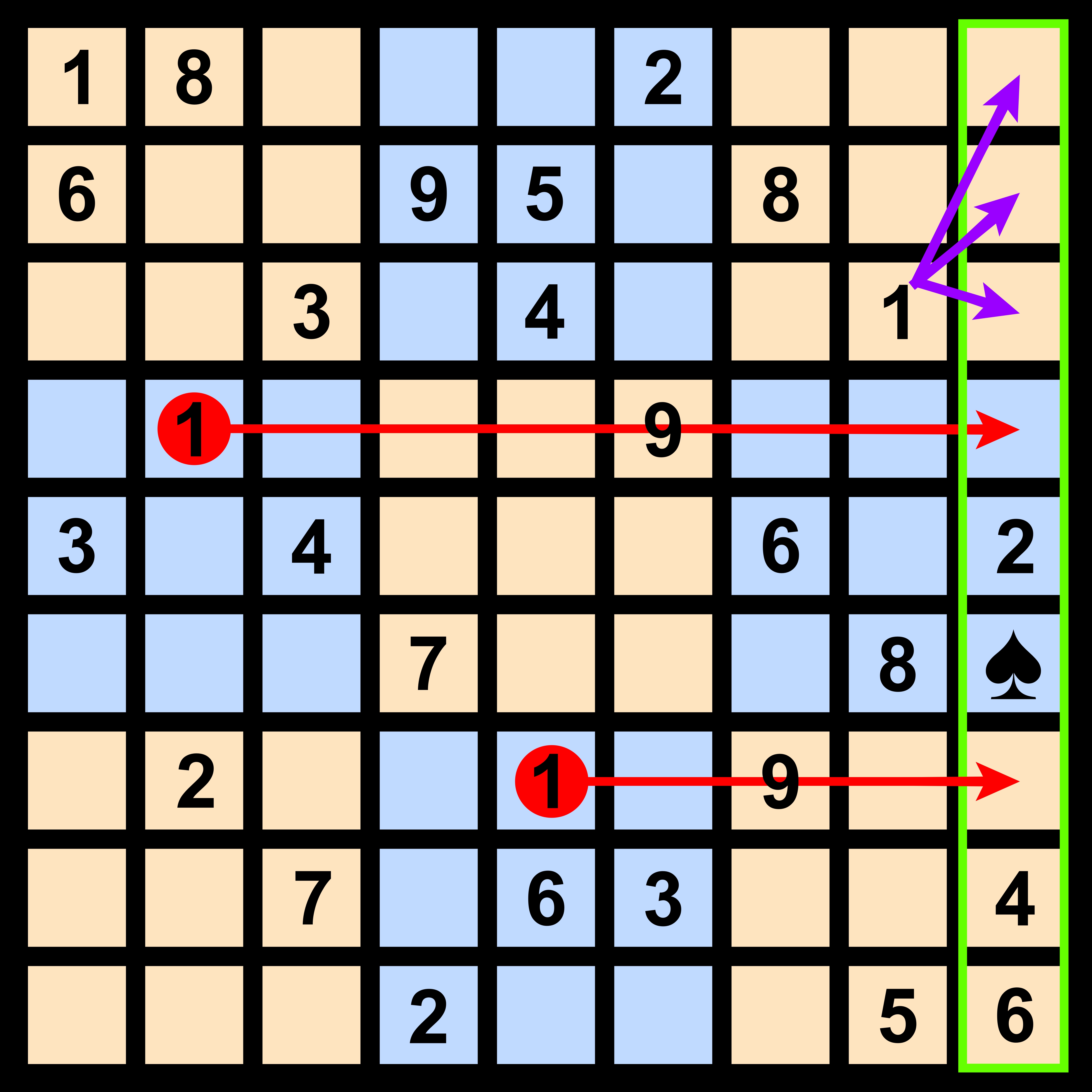
▼로 나타낸 세로줄 어디에 1이 들어갈지를 생각해 보면 ♠칸밖에 없음을 알 수 있다. 왜냐하면 오른쪽 위 블록에는 이미 1이 있어서 1번째, 2번째, 3번째 칸은 안되고, 4번째와 7번째 칸은 가로줄에 1이 있다.
5-3. 특정 칸에 주목하는 방법
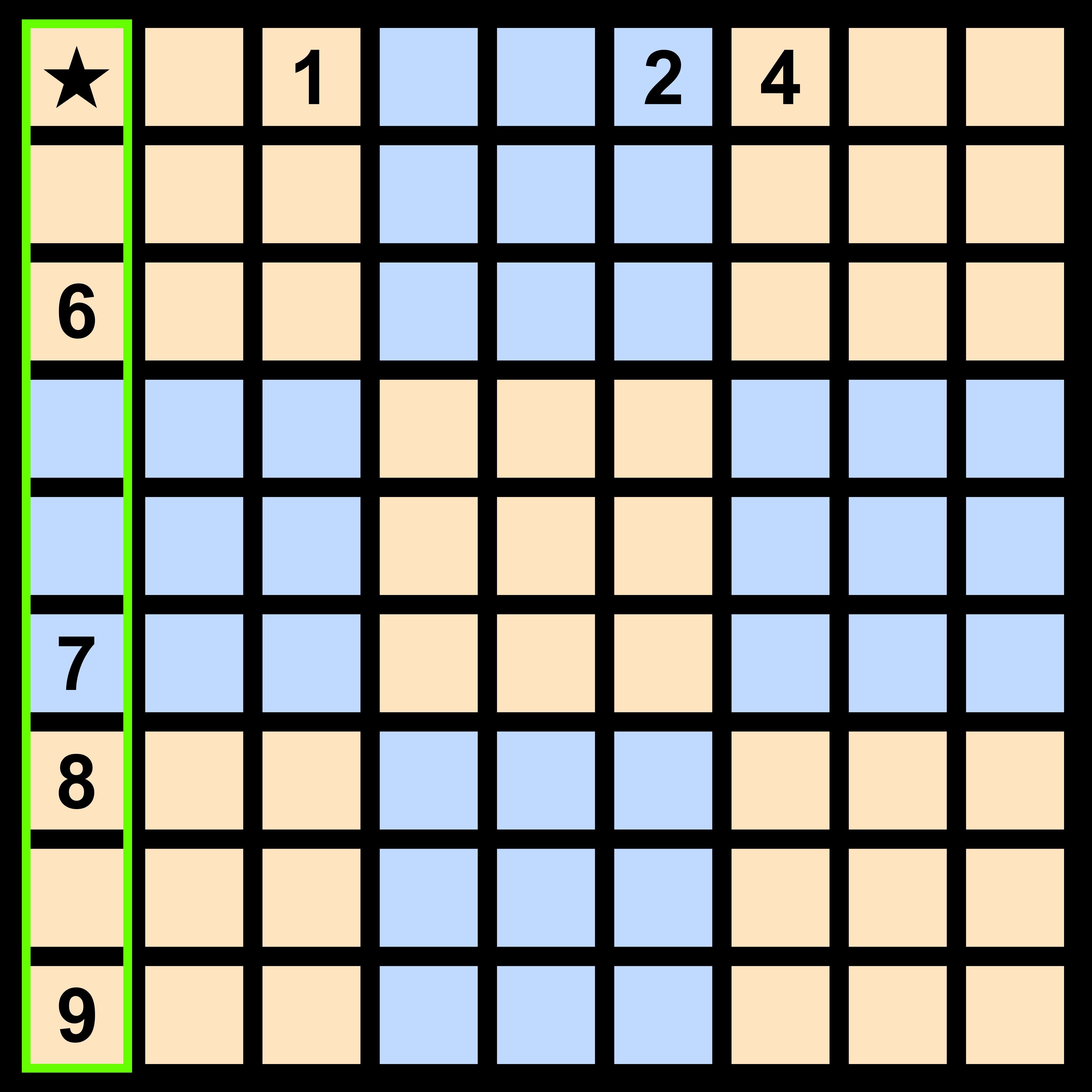
★칸에 주목해 보자. 가로줄에는 1, 2, 4, 세로줄에는 6, 7, 8, 9 같은 블록에는 3이 있다. 따라서 ★에는 5가 들어간다.
5-4. 어떻게 하든 이론
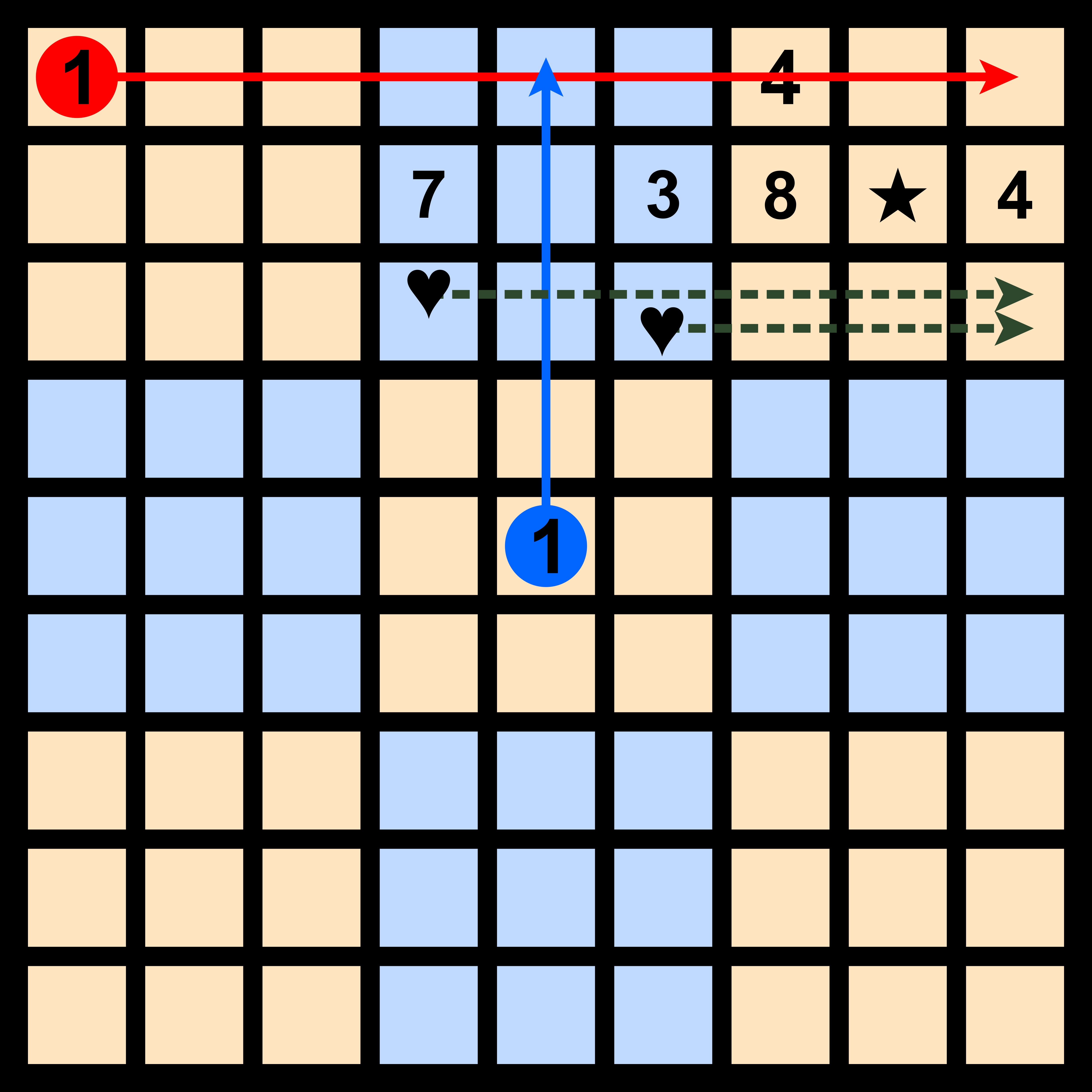
가운데 위의 블록 어디에 1이 들어갈지를 생각해 보자. 빨간색 세로줄과 파란색 가로줄에는 1이 들어가지 않기 때문에 ♥로 표시된 2개의 칸 어딘가에 들어간다. 어떻게 하든 오른쪽 위 블록의 초록색 점선이 지나가는 곳에 1은 들어갈 수 없다. '특정 블록에 주목하는 방법'에 따라, 오른쪽 위 블록의 어디에 1이 들어갈지를 생각하면 ★에 1이 들어간다.
5-5. 쌍둥이법
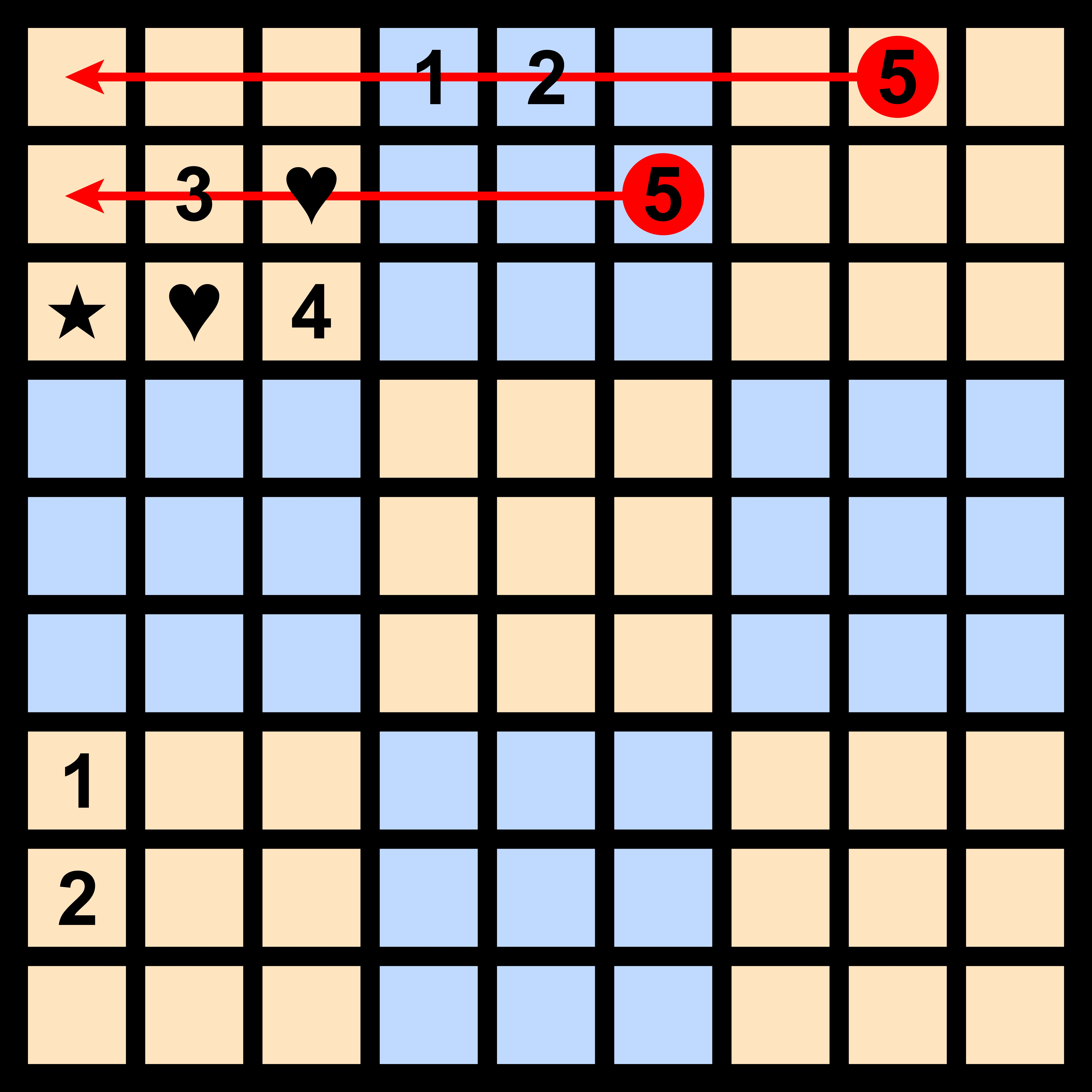
먼저 '왼쪽 위 블록' 어디에 1과 2를 넣을지를 생각한다. 세로줄과 가로줄에 1과 2가 없는 ♥로 표시된 2개의 칸에 각각 1이나 2 어느 한쪽에 들어간다. 즉 2개의 ♥칸은 1과 2로 '예약'되어, 그 외의 숫자는 들어갈 수 없음을 확정한다. 이어서 '특정 블록에 주목하는 방법'에 따라, 왼쪽 위의 블록 어디에 5가 들어갈지 생각한다. ♥칸에는 1이나 2가 들어가기 때문에 5는 들어갈 수 없고, 가로줄에 5가 있는 칸(빨간색 화살표가 지나는 칸)에도 5가 들어갈 수 없다. 따라서 ★에 5가 들어감을 알 수 있다. 이와 같은 방식으로 다른 빈칸의 숫자를 좁혀 나가는 방법을 '쌍둥이법'이라고 하며 흔히 사용된다.
마찬가지로 3개의 칸에 3종의 숫자 가운데 어느 하나가 들어가는 '세쌍둥이법'도 있다.
5-6. 이게타 이론
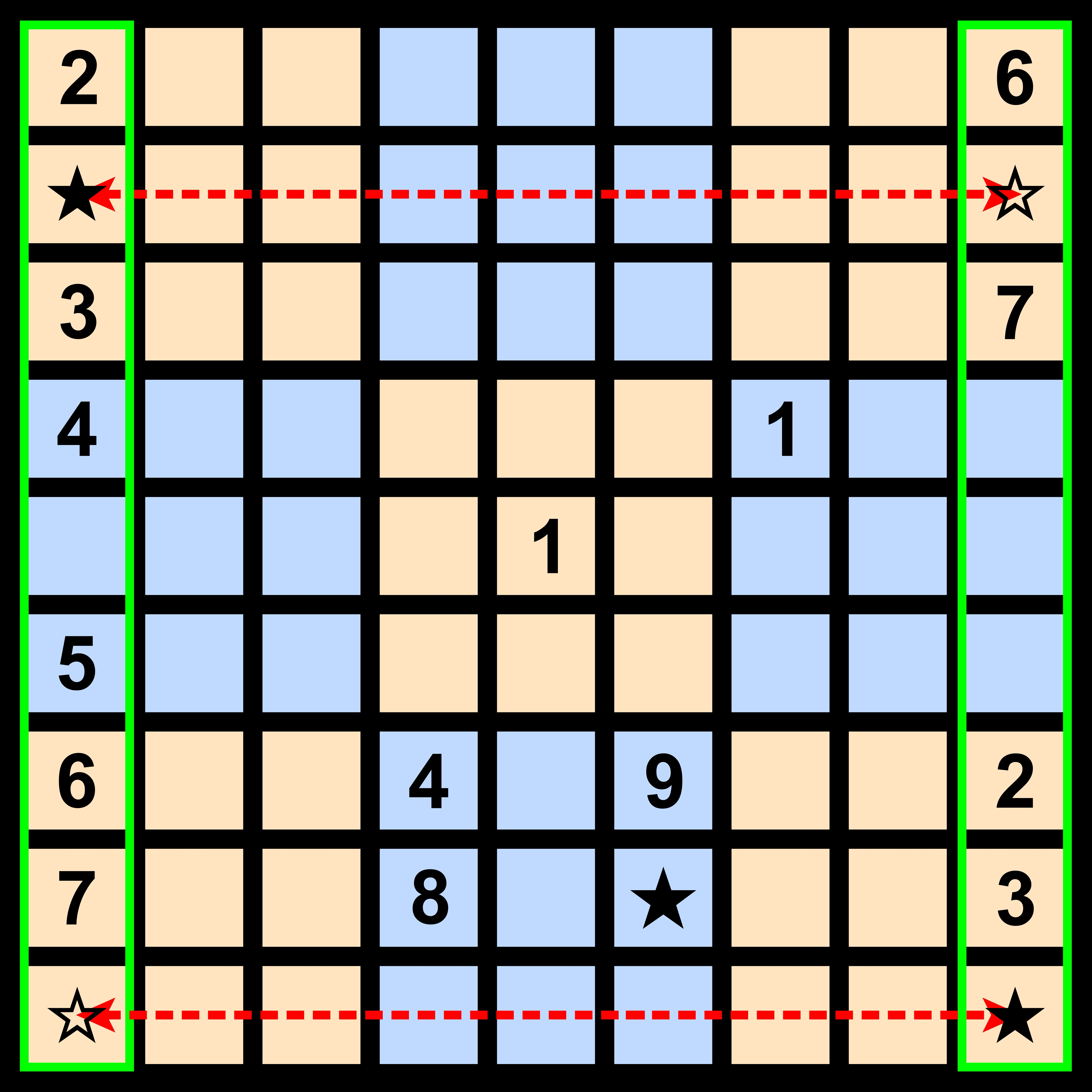
'특정 블록에 주목하는 방법'에 따라 형광색으로 표시된 2개의 세로줄 어디에 1이 들어갈지를 생각한다. 그러면 ★으로 표시된 2개의 칸에 1이 들어가든지, 아니면 ☆으로 표시된 2개의 칸에 1이 들어가든지 둘 중 하나임을 알 수 있다. 어떻게 하든 초록 점선 위에는 1이 들어갈 수 없다. '특정 열 또는 행에 주목하는 방법'에 따라 가운데 아래 블록 어디에 1이 들어갈지를 생각하면 ★에 1이 들어간다.
5-7. 그 외의 방법
'황새치'나 '해파리', 'XY 체인' 등 재미있는 이름을 가진 해법도 여러 가지가 있다.