'커뮤니티'를 찾는 알고리즘
0. 목차
- 노드로 사회 연결망을 한눈에 파악한다.
- 연결망 내에서 커뮤니티 찾기의 다양한 응용 가능성
- 가라데 클럽 연결망
- 커뮤니티 찾는 두 가지 방법
- 모든 가능한 조합을 남김없이 시도해 보는 방법
- 커뮤니티를 찾는 현실적인 방법
- 겹치는 커뮤니티를 찾는 방법

1. 노드로 사회 연결망을 한눈에 파악한다.
현대의 많은 사람들은 '페이스북(FaceBook)', '트위터(Twitter)', '카카오톡(Kakao Talk)', '유튜브(Youtube)' 등 '누리소통망(Social Networking, 소셜 네트워크)'을 자주 이용한다. 이 '누리소통망' 내에서 자기 자신은 상호 관계의 연결망을 쉽게 알 수 있고, 친한 친구들도 내가 어떤 인간관계를 맺고 있는지를 잘 알 수 있을 것이다. 하지만 제3자가 내 사회관계의 연결망이 어떤 구조로 서로 중첩되고 얽혀있는지 알아채기는 어렵다. 그래서 누가 누구와 연결되어 있는지, 즉 '연결선(Link)'의 유무라는 정보만을 이용해서, 연결망 안에서 사람들이 어떤 '커뮤니티(Community)' 구조를 갖고 있는지를 객관적이고 정량적인 방법으로 살펴보는 방법을 살펴볼 것이다. 각자는 특정 커뮤니티에 속해 있으므로, 이렇게 구성된 커뮤니티가 모여 전체 연결망을 구성한다고 생각할 수도 있다. 사람 하나하나를 '노드(Node)'하여 연결망을 그리면 노드가 너무 많아 정말 복잡해 보이는 연결망이 얻어진다. 하지만 커뮤니티를 노드로 해서 다시 그리면 직관적으로 더 쉽게 전체 구조를 한눈에 파악할 수 있는 연결망을 얻을 때도 많다.
2. 연결망 내에서 커뮤니티 찾기의 다양한 응용 가능성
연결망 내에서 커뮤니티 찾기는 다양한 응용 가능성이 있다. 몇 가지 예를 들어보자.
국회의원들은 같은 정당뿐 아니라, 다른 정당의 의원과도 다양한 방식으로 서로 교류하고 있을 것임에 분명하다. 국회의원 개인 한 명 한 명이 다른 의원과 맺고 있는 관계의 데이터를 모아서 국회의원 전체의 연결망을 그려보고, 그 안의 커뮤니티를 찾아볼 수 있다. 아마도 이렇게 찾은 커뮤니티는 의원들의 소속 정당과 겹치는 경우가 대부분일 테지만, 그렇지 않은 국회의원도 있을 수 있다. 이런 분은 어쩌면 소속 정당을 다른 정당으로 바꿀 가능성이 큰 사람이라고 생각할 수도 있다. 그리고 정당을 바꾼다면, 어느 정당으로 옮겨갈지도 예상해 볼 수 있다.
제2차 세계대전이 발발하기 이전의 유럽의 여러 나라 사이의 관계를 당시 신문 기사를 이용해 모아 연결망으로 만들 수 있다. 이렇게 만들어진 연결망 구조를 이용해 커뮤니티를 찾으면, 여러 나라들이 서로 연합해 두 개의 그룹으로 나뉠 때 어느 나라가 어느 동맹에 편입할지 예측할 수도 있다. 이처럼, 연결망 안의 커뮤니티를 찾아보는 것은 재밌고도 중요한 연구 방법이다.
3. 가라데 클럽 연결망
연결망 내에서 커뮤니티를 찾는 새로운 알고리즘을 제안한 과학자는 자신의 방법이 제대로 작동하는지 확인하고 싶어한다. 네트워크 과학자가 이럴 때 사용하는 표준적인 데이터가 있다. 바로 '자키리의 가라데 클럽(Zachary's Karate Club)' 연결망이라는 공개된 데이터다. 1970년대에 '웨인 자카리(Wayne W. Zachary)'는 한 대학교의 '가라데 클럽'에 속한 멤버들이 클럽 밖에서 누가 누구와 만나는지를 조사했다. 34명의 멤버 각각을 노드로 하고, 이들 사이의 관계를 유무로 표시하는 78개의 링크를 자지고 연결망을 그려볼 수 있다. 다만 이렇게 그린 연결망만으로는 이 안에 어떤 커뮤니티가 있는지 한눈에 알기 어렵다.

3-1. '가라데 클럽' 내부에 갈등이 커져 둘로 나뉘었다.
그런데 '웨인 자카리'가 이 연구를 진행하던 중 '가라데 클럽(Karate Club)'에 흥미로운 일이 발생했다. '가라데 클럽' 내부에 갈등이 커져, '대표가 이끄는 클럽'과 '사범이 이끄는 클럽' 둘로 나뉘게 된 것이다. 여기서 재미있는 질문을 할 수 있다. '클럽이 둘로 쪼개지기 전의 멤버들 사이의 사회관계만을 이용해서, '대표가 이끈는 클럽'과 '사범이 이끄는 클럽' 둘 중 어느 클럽으로 각각의 멤버가 옮겨갈지를 예측할 수 있을까?
클럽이 둘로 나뉘기 전의 사회연결망에서 두 개의 커뮤니티를 알고리즘을 이용해 찾아보고, 그 결과를 누가 어느 클럽에 합류했는지에 대한 실제 자료와 비교해 보는 것이다. '클럽이 쪼개진 뒤 각 멤버가 실제로 속한 새 클럽'과 '알고리즘이 찾은 커뮤니티'가 일치할수록 알고리즘의 정확도가 높다고 판단할 수 있다. 이와 같은 방법으로, '자카리의 가라데 클럽 연결망'은 커뮤니티를 찾는 알고리즘의 벤치마크 테스트로 널리 이용된다.

3-2. 자카리 가라데 클럽 클럽
'자카리 가라데 클럽 클럽(Zachary's Karate Club Club)'이라는 이름의 클럽도 있다. 클럽이라는 단어가 두 번 중복된 오타가 아니라, 정말 이런 클럽이 있다. 그런데 '자카리 가라데 클럽 클럽'의 멤버 선정 기준이 재밌다. 네트워크에 관련된 학회가 열리 때, 학회 기간 중의 발표에서 가장 먼저 자카리의 가라데 클럽 연결망을 언급한 과학자가 '자카리 가라데 클럽 클럽'의 새 멤버가 된다.
트로피도 있다. 새 멤버가 된 과학자는 바로 직전에 멤버가 되었던 사람으로부터 트로피를 전달받고, 다음 멤버가 정해지기 전까지 트로피를 소장한다. 아래의 사진은 2013년 인디아나 대학교의 안용렬 교수가 세 번째 트로피 수상자가 되어 '메이슨 포터(Mason Porter)' 교수에게서 트로피를 전달받는 모습이다. 과학자들도 사람이기에, 이런 재밌는 장난 같은 일도 많이 벌인다. 아마 또 누군가는 '자카리 가라데 클럽 클럽'의 멤버 사이의 연결망을 나중에 만들어보려고 데이터를 이미 모으고 있을지도 모르는 일이다. 만약 그러면 '자카리 가라데 클럽 클럽 연결망'이 되는 것이다.

4. 커뮤니티 찾는 두 가지 방법
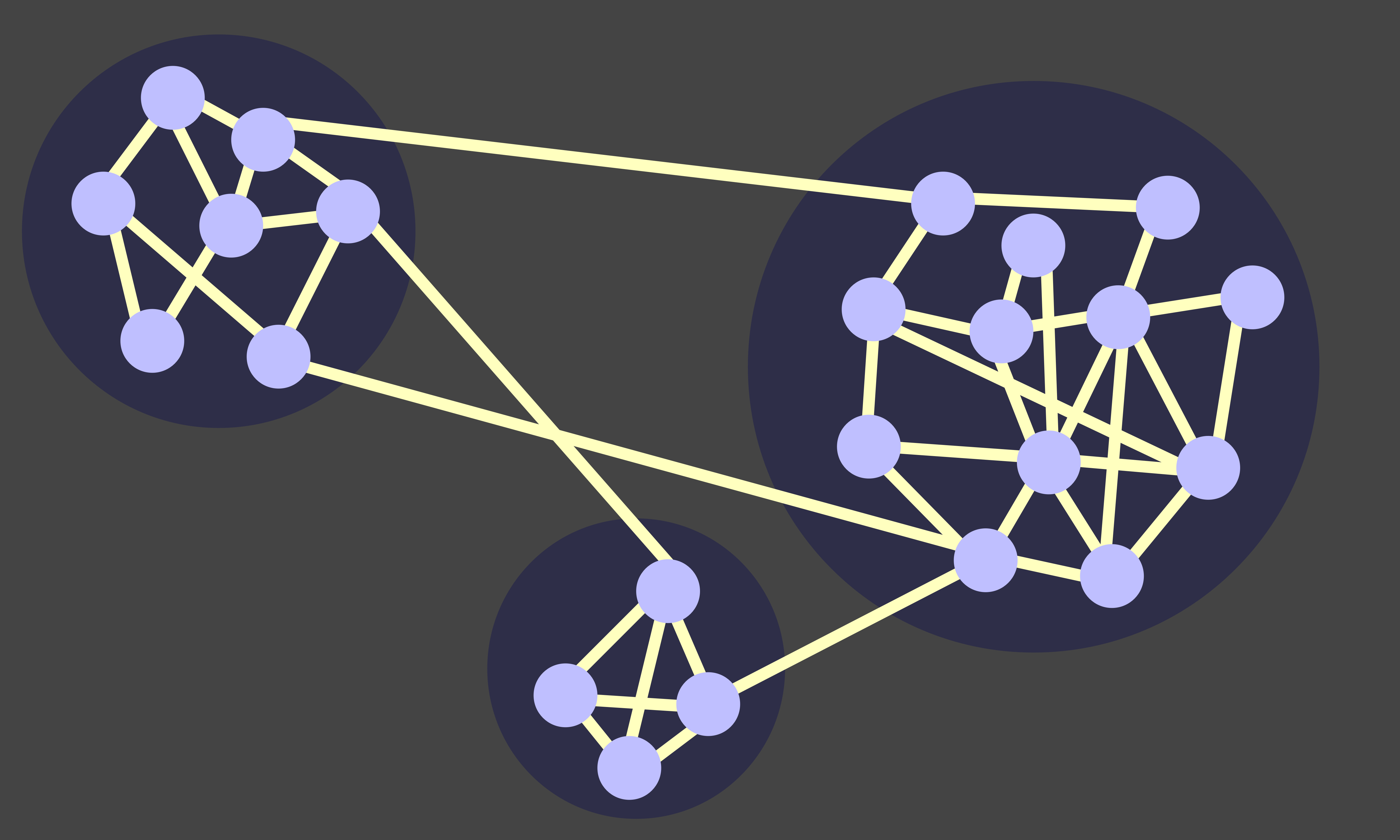
연결망 안에서 커뮤니티를 찾는 방법은 아래의 그림을 보면 직관적으로는 쉽게 이해할 수 있다. 한 커뮤니티에 속한 노드와는 관계가 밀접하지만, 다른 커뮤니티에 속한 노드와는 그렇지 않다. 즉, 커뮤니티가 제대로 찾아졌다면 '커뮤니티 안의 링크'의 밀도는 '커뮤니티를 가로지르는 링크'의 밀도보다 더 클 것이 분명하다. 커뮤니티를 찾는 방법은 크게 둘로 나뉜다.
- 첫째, 모든 가능한 조합을 남김없이 시도해 보는 방법으로, 정확하지만 시간이 오래 걸리는 무지막지한 방법이다.
- 둘째, 근사적으로 커뮤니티를 찾지만 시간이 짧게 걸리는 방법이다.
최근에는 당연히 둘째 방법이 더 널리 쓰인다. 현실의 대부분의 연결망은 워낙 커서, 정확하지만 오래 걸리는 방법으로 커뮤니티를 찾는 것이 불가능에 가깝기 때문이다.
5. 모든 가능한 조합을 남김없이 시도해 보는 방법
예를 들어보자. 크기가 N인 연결망에 각각 크기가 N1, N2인 두 개의 커뮤니티 있다고 하자. 이때 전체 노드를 두 커뮤니티로 나누는 방법은 N!/(N1!×N2!)가지가 있다. 연결 망에서 가능한 커뮤니티 구성의 경우의 수는 연결망의 크기가 커질수록 천문학적인 숫자로 커진다. 크기가 34인 '자카리 가라데 클럽'안에 크기가 각각 17인 두 개의 커뮤니티가 있다는 정보가 주어져 있더라도, 어느 노드가 어느 커뮤니티에 속하는지에 대해 생각해 볼 수 있는 모든 경우의 수는 34!/(17!×17!)로 약 '20억' 정도다. 이마저도 사실 매우 단순한 경우다. 커뮤니티가 두 개라는 조건, 그리고 각각의 크기가 17로 딱 주어진 경우다.
일반적인 경우에는 N이 상당히 클뿐더러, 몇 개의 커뮤니티가 있는지, 그리고 커뮤니티 각각의 크기가 얼마인지도 알려져 있지 않은 상황에서 커뮤니티를 찾아야 한다. 크기가 N인 연결망에서 모든 노드를 임의의 개수의 임의의 크기의 커뮤니티로 나누는 경우는 '벨 수(Bell Number)'라고 불리는데, 크기가 34인 가라데 연결망이라면 그 값이 거의 1030에 육박한다. 즉, 모든 가능한 경우를 하나씩 조사해 보는 방법은, 정확하지만 시간이 오래 걸린다. 따라서 연결망이 자주 등장하는 현실의 문제에서는 직접 적용하는 것이 불가능하다. 커다란 연결망의 커뮤니티를 정확하게 찾는 것은 어려운 일이다.
6. 커뮤니티를 찾는 현실적인 방법
하지만 좀 더 생각해 보면, 주어진 연결망 데이터에도 다양한 이유로 이미 오류가 있을 수 있다. 따라서 어차피 정확한 커뮤니티를 찾는 것은 사실 큰 의미가 없을 수도 있다. 대규모 연결망에서 커뮤니티를 찾는 방법에 대한 연구는 상당히 빠르게 발전해 왔다. 이제는 과학적인 연구주제라기보다는 이미 공학적인 연구로 바뀐 느낌이다.
물리학 분야에서 '복잡한 연결망'에 대한 연구가 시작되던 시기에 '커뮤니티를 찾는 방법'에 대한 흥미로운 논문들이 등장했다. 특히 미시간 대학 '마크 뉴만(Mark Newman)' 교수가 이끄는 연구그룹에서 중요한 논문을 연이어 발표했다. 당시 이미 컴퓨터 과학 분야에서 커뮤니티를 찾는 다양한 알고리즘이 개발되어 있었지만, 물리학자들이 이 분야에 큰 관심을 갖기 시작한 것은 '마크 뉴만'의 연구 부터였다.
6-1. 저반-뉴만 알고리즘
위에서 보았던 '연결망 안 커뮤니티' 그림을 다시 보자. 이 간단한 연결망의 모든 노드에 사람이 살았다고 생각해 보자. 그리고 연결망의 링크는 사람들이 이동하는 길이라고 상상해 보자. 동그라미로 테두리를 표시한 세 개의 커뮤니티는 사람들이 모여 사는 세 마을이라고 생각해도 좋겠다. 각자는 다른 사람 모두를 한 명씩 한 명씩 연결망의 길인 링크를 따라 걸어서 방문해 다시 집으로 돌아온다고 해보자. 모든 사람이 방문을 마치고 나면, 많은 사람이 걸어서 발자국이 많이 찍힌 길도 있고, 발자국이 얼마 없는 길도 있다. 그러면 어떤 길 위에 발자국이 많을까? 한마을 안의 골목길에는 발자국이 별로 없지만, 마을과 마을과 연결하는 길에는 발자국이 많을 것임을 쉽게 짐작할 수 있다. 사람들이 길을 이리저리 돌아다니기만 해도, '동네 안 골목길'보다 '옆 마을로 건너가는 큰 길'에 발자국이 많이 찍힐 수밖에 없다.
'저반-뉴만의 알고리즘(Girvan-Newman's Algorithm)'은 바로 이 '길 위에 찍힌 발자국 수'를 이용한다. 먼저, 연결망의 모든 길에 얼마나 많은 발자국이 찍혔는지를 센다. 그러고 가장 많은 발자국이 찍힌 링크를 지우는 거다. '연결망 안 커뮤니티' 그림의 연결망에 이 방법을 적용하면, 마을 안의 길보다는 두 마을을 연결하는 길이 가장 먼저 사라질 것임을 쉽게 예상할 수 있다. '저반-뉴만의 알고리즘'에서는 발자국이 가장 많은 길을 지운 후, 길 위의 발자국 수를 다시 세어서 다음에 없앨 길을 또 정한다. 이 과정을 계속 반복하다 보면, 연결망의 링크가 하나씩 하나씩 지워지게 된다. 이렇게 링크를 지워가면서 전체 연결망이 부분으로 나뉘는 것을 주시하며, 적절한 개수의 커뮤니티로 나뉠 때 계산을 멈추게 된다. '연결망 안 커뮤니티' 그림의 경우를 생각하면, 발자국이 많은 처음 몇 길을 지우면, 결국 3개의 마을이 각각 고립될 것을 예상할 수 있다. 이렇게 고립시킨 마을 하나하나가 바로 연결망의 커뮤니티라고 할 수 있다.
6-2. 모듈성 최대화 알고리즘
'마크 뉴만(Mark Newman)'은 이후 '모듈성 최대화 알고리즘(Modularity Maximization Algorithm)'이라는 방식도 제안했다. 바로 '모듈성(Modularity)'이라는 양을 정의하고 이 값을 가장 크게 하는 알고리즘이다. 만약 알고리즘이 제대로 커뮤니티를 찾았다면, 한 커뮤니티 안에 들어 있는 두 노드 사이에는 링크가 존재할 가능성이 크다. 하지만 '크다'라고만 말하면 안 되고, 그것이 무엇에 비해서 큰 것인지 비교의 대상을 함께 이야기해야 한다. '마크 뉴만'이 제안한 비교 대상은 바로, 마구잡이로 링크가 아무 곳에나 연결되어 있는 마구잡이 연결망의 상황이다. 즉, 한 커뮤니티에 있는 두 노드를 고르고는, 둘을 연결하는 링크가 존재한다면 그 가능성이 마구잡이로 노드들을 연결할 때보다 더 큰지를 보는 것이다. 이 계산을 '연결망의 모든 노드'에 대해 수행하면서 그 합을 구한 것이 바로 모듈성 M이다. M의 값이 가장 커지도록 노드의 소속을 바꿔가다 보면, 결국 연결망 안의 커뮤니티를 찾게 된다.
'저반-뉴만 알고리즘'보다 '모듈성 최대화 알고리즘'이 더 좋은 점이 있다. '저반-뉴만의 알고리즘'에서는 커뮤니티의 개수를 알고리즘의 내부에서 정하기가 어려운데 비해서, '모듈성 최대화 알고리즘'에서는 모듈성 M이 최대가 되는 커뮤니티의 개수도 알고리즘의 내부에서 찾을 수 있다. 모듈성을 이용해 커뮤니티를 찾는 방법은 지금도 가장 널리 이용되는 알고리즘이다.
7. 겹치는 커뮤니티를 찾는 방법
'모듈성 최대화 알고리즘'으로 커뮤니티를 찾을 대는 연결망의 한 노드가 딱 하나의 커뮤니티에 속하게 된다. 하지만 조금만 생각해 보면, 실제로는 한 사람이 여러 커뮤니티에 동시에 속하는 상황이 오히려 더 자연스럽다는 것을 알 수 있다. 그래서 연결망의 노드 하나가 여러 커뮤니티에 속하는 것이 가능한 그런 알고리즘도 여럿 개발되어 있다. 그중 여기에서는 2가지만 소개한다.
7-1. 링크 클러스터링 방법
안용렬 교수가 제안한 '링크 클러스터링(Link Clustering)' 방법은 '노드(Node)'가 아닌 '링크(Link)'를 그룹으로 나누는 재밌는 방법이다. 즉, 한 노드에 연결되어 있는 링크는 여럿이니, 노드가 속한 커뮤니티도 여럿이 가능한 그런 방법이다. 페이스북에서 친구 관계를 생각해 보면, 나와 다른 한 친구의 관계의 속성은 상당히 명확할 때가 많다. 즉, 나는 여러 커뮤니티에 속할 수 있지만, 특정 친구의 관계는 딱 하나의 속성을 가질 때가 많다. 바로 이 아이디어를 이용한 것이 안용렬 교수의 방법이다.
7-2. 덩이 굴리기 방법
'링크 클러스터링(Link Clustering)' 방법과 마찬가지로, '덩이 굴리기(Clique Percolation)'라고 부를 수 있는 방법도 한 노드가 한 개 이상의 커뮤니티에 속할 수 있다.